- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
 (1)
– система булевых функций.
(1)
– система булевых функций.
Система (1) называется полной, если любую булеву функцию можно реализовать формулой в этой системе.
Примером полной системы является сам класс булевой функции.

Пусть даны две системы булевых функций

 (1)
(1)
 (2)
(2)
относительно которых известно, что (1) – полная система и каждая функция первой системы представляется в виде суперпозиции функций (2) системы, тогда (2) – полная система.
Система (1) называется функционально замкнутым классом, если любая суперпозиция функций этой системы принадлежит ей же.
Функционально
замкнутые классы отличные от пустого
класса и от класса
 называютсясобственными
функционально замкнутыми классами.
называютсясобственными
функционально замкнутыми классами.
Рассмотрим важнейшие функционально замкнутые классы.
1.
 - это класс функций, сохраняющий ноль,
т. е. функций для которых
- это класс функций, сохраняющий ноль,
т. е. функций для которых
 Пример.
Пример.
 .
.
2.
 - это класс функций, сохраняющий единицу,
т. е. функций для которых
- это класс функций, сохраняющий единицу,
т. е. функций для которых
 Пример.
Пример.
 .
.
3.
 - это класс линейных функций, т. е.
функции, для которых полином Жегалкина
является линейным относительно каждой
переменной.
- это класс линейных функций, т. е.
функции, для которых полином Жегалкина
является линейным относительно каждой
переменной.
 .
.
4.
 - это класс монотонных функций
- это класс монотонных функций
Пусть
 ,
где
,
где
 - двоичные векторы,
- двоичные векторы,
являющиеся
наборами значений переменных

 ;
;

Вектор
 предшествует или младше вектора
предшествует или младше вектора ,
если
,
если
 ,
такиенаборы
называются
сравнимыми.
,
такиенаборы
называются
сравнимыми.
Свойства отношений.
1)
 - рефлексивность
- рефлексивность
2)
 и
и
 - симметричность
- симметричность
3)
 и
и
 - транзитивность
- транзитивность
Булева
функция
называется монотонной,
если
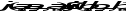 для каждой пары сравнимых наборов.
для каждой пары сравнимых наборов.
Пример монотонных функций.
1)



2)



5.
 - это класс самодвойственных функций,
для которых
- это класс самодвойственных функций,
для которых
Теорема Поста. Для того чтобы система булевых функций (1) была полной необходимо и достаточно, чтобы она целиком не содержалась ни в одном из пяти функционально замкнутых классов.
Для
проверки полноты системы функций
 составляется специальная критериальная
таблица:
составляется специальная критериальная
таблица:
|
|
|
|
|
|
|
|
|
+ |
- |
- |
+ |
- |
|
|
+ |
- |
+ |
- |
- |
|
|
|
|
|
|
|
|
|
- |
+ |
+ |
+ |
- |
По теореме Поста система является полной, если каждый столбец таблицы содержит хотя бы один « - ».
40. Графы и их свойства
Графические представления - удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений. Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы, изучаемые в теории графов. Теория графов основана на работе с конечными множествами.
Графическое представление в узком смысле – это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий – ребер или дуг. Графы и их составляющие характеризуются определенными свойствами и набором допустимых преобразований (операций) над ними.
Графом
G
называется
совокупность двух множеств: вершин
 и ребер
и ребер :
: .
.
Ребрами графов наз-ся отрезки, концами которых явл-ся вершины.
Между
элементами мн-ва
 введемотношение
смежности:
две вершины графа наз-ся смежными,
если они соединены одним ребром.
введемотношение
смежности:
две вершины графа наз-ся смежными,
если они соединены одним ребром.
Между
элементами мн-ва
 и мн-ва
и мн-ва определеноотношение
инцидентности
– вершина А и ребро
определеноотношение
инцидентности
– вершина А и ребро
 наз-ся инцидентными, если вершина А
явл-ся концом ребра
наз-ся инцидентными, если вершина А
явл-ся концом ребра ( или ребро
( или ребро выходит из вершиныА) .
выходит из вершиныА) .
Ребро, соединяющее две вершины, может иметь направление от одной вершины к другой; в этом случае оно называется направленным, или ориентированным, или дугой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.
Граф наз-ся обыкновенным, если он не содержит кратных ребер и петель.
Граф, заданный мн-ом вершин и дуг, называется ориентированным (орграфом).
Ребра, инцидентные одной и той же паре вершин, называются параллельными, или кратными. Граф, содержащий кратные ребра, именуется мультиграфом. Ребро, концевые вершины которого совпадают, называется петлей.
Граф
называется конечным,
если множество его элементов (вершин
и ребер) конечно, и пустым,
если его множество вершин А (а значит
и ребер
 )
пусто. Обыкновенный граф именуется
полным, если каждая пара вершин соединена
ребром.
)
пусто. Обыкновенный граф именуется
полным, если каждая пара вершин соединена
ребром.
Дополнением
графа G
называется граф
 ,
имеющий те же вершины, что и графG,
и содержащий только те ребра, которые
нужно добавить к графу G,
чтобы получить граф.
,
имеющий те же вершины, что и графG,
и содержащий только те ребра, которые
нужно добавить к графу G,
чтобы получить граф.
Каждому неориентированному графу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направления.
Локальной
степенью
(или просто степенью) вершины
 н-графаG
называется количество ребер, инцидентных
данной вершине-
н-графаG
называется количество ребер, инцидентных
данной вершине-
 .
.
Вершина, не соединенная ни с одной вершиной, наз-ся изолированной. Ее степень равна 0.
Вершины
графа, степени которых четные числа,
наз-ся четными вершинами, а вершины
графов, степени которых нечетные –
нечетные вершины. Введем обозначения:
 - число вершин,
- число вершин, -
число ребер,
-
число ребер, -
вершины графа,
-
вершины графа, -
ребра графа.
-
ребра графа.
Сумма
степеней всех вершин графа явл-ся четным
числом и равна удвоенному количеству
ребер

Типы и способы задания.
Задать
граф – значит описать множества его
вершин и ребер, а также отношение
инцидентности. Для описания вершин и
ребер достаточно их занумеровать. Пусть
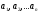 вершины
графаG;
вершины
графаG;
 ребра.
Помимо этого графы можно задавать с
помощью специальным образом построены
матриц двух типов:
ребра.
Помимо этого графы можно задавать с
помощью специальным образом построены
матриц двух типов:
Матрицей инцидентности
 , причем каждый элемент определяется
следующим образом:
, причем каждый элемент определяется
следующим образом: .
Такая матрица явл-ся бинарной; в общем
случае прямоугольная порядка
.
Такая матрица явл-ся бинарной; в общем
случае прямоугольная порядка ;
в каждом столбце матрицы не более двух
единиц, т.к. ребро инцидентно только
двум вершинам
;
в каждом столбце матрицы не более двух
единиц, т.к. ребро инцидентно только
двум вершинамМатрицей смежности
 ,
каждый элемент которой определяется
следующим образом:
,
каждый элемент которой определяется
следующим образом:
 .Эта
матрица всегда квадратная порядкомn,бинарная
(состоит из 0 и 1), на главной диагонали
все элементы 0, симметрична относительно
главной диагонали, сумма всех элементов,
стоящих либо в строке или столбце,
определяет степень соответствующей
вершины
.Эта
матрица всегда квадратная порядкомn,бинарная
(состоит из 0 и 1), на главной диагонали
все элементы 0, симметрична относительно
главной диагонали, сумма всех элементов,
стоящих либо в строке или столбце,
определяет степень соответствующей
вершины
 .
.
Кроме
того, для любого геометрического графа
 единственнаяабстрактная
интерпритация
– это набор из трех объектов
единственнаяабстрактная
интерпритация
– это набор из трех объектов
 ,
где
,
где функция инцидентности:
функция инцидентности: ,
т.е. в качестве инцидента выступают
ребра графа, а значениями этой ф-и явл-ся
вершины графа, инцидентные данному
ребру. Для любого абстрактного графа
существует целое мн-во соответствующих
геометрических графов.
,
т.е. в качестве инцидента выступают
ребра графа, а значениями этой ф-и явл-ся
вершины графа, инцидентные данному
ребру. Для любого абстрактного графа
существует целое мн-во соответствующих
геометрических графов.
В теории графов понятие равенства заменено термином изоморфизм.
Два
графа
 и
и - изоморфные
- изоморфные ,
если выполняется равенство
,
если выполняется равенство ,
где
,
где - биективные отображения – функции
композиций двух функций. Т.е. графы
изоморфны
- биективные отображения – функции
композиций двух функций. Т.е. графы
изоморфны после
применения каждой из этих композиций
получаются одни и те же вершины.
Композицией нескольких функций наз-ся
последовательное изменение каждой из
этих функций, причем аргументом каждой
последующей функции явл-ся значение
предыдущей. Для установления изоморфности
отображения чаще всего задают с
использованием номерования, т.е.
после
применения каждой из этих композиций
получаются одни и те же вершины.
Композицией нескольких функций наз-ся
последовательное изменение каждой из
этих функций, причем аргументом каждой
последующей функции явл-ся значение
предыдущей. Для установления изоморфности
отображения чаще всего задают с
использованием номерования, т.е.
 .
Но такой метод не всегда эффективен, и
в случае сложных графов задача проверки
изоморфизма еще не решена.
.
Но такой метод не всегда эффективен, и
в случае сложных графов задача проверки
изоморфизма еще не решена.
Операции над частями графа.
Граф
Н называется частью графа G,
 ,
если множество его вершинA(H)
и ребер U(H)
является подмножеством множеств вершин
A(G)
и ребер U(G)
соответственно, т.е.
,
если множество его вершинA(H)
и ребер U(H)
является подмножеством множеств вершин
A(G)
и ребер U(G)
соответственно, т.е.
 .
.
Над частями графа G могут производиться следующие операции:
Дополнение
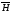 к части Н – определяется множеством
всех ребер графаG,
не принадлежащих Н: U(H)
к части Н – определяется множеством
всех ребер графаG,
не принадлежащих Н: U(H) ,
, ;
;Сумма
 частей
частей и
и графаG:
графаG:
 и
и ;
;
Произведение
 :
:
 и
и
 .
.
Две
части
 и
и непересекаются
по вершинам,
если они не имеют общих вершин
непересекаются
по вершинам,
если они не имеют общих вершин
 ,
а значит , и общих ребер
,
а значит , и общих ребер .
Части
.
Части и
и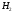 не пересекаются
по ребрам,
если
не пересекаются
по ребрам,
если
 .
Если
.
Если ,
то сумма
,
то сумма называетсяпрямой.
называетсяпрямой.
Последовательность ребер, в которой каждая пара соседних имеет общую вершину, наз. маршрутом.
Путем
из вершины
 в
в наз. такой соединяющий маршрут, в котором
каждое ребро не встречается более
одного раза.
наз. такой соединяющий маршрут, в котором
каждое ребро не встречается более
одного раза.
Две вершины графа наз-ся связными, если существует маршрут, их соединяющий. На множестве всех вершин графа можно ввести отношение связности:
рефлексивность – любая вершина графа сама с собой связна;
симметричность – если вершина а связна с вершиной b, то и вершина b связна с вершиной а.
транзитивность - если вершина а связна с вершиной b, и вершина b связна с вершиной с, то вершины а и с связны, т.е. существует маршрут
 .
.
Отношение
связности явл-ся отношением
эквивалентности разбивает
любое множество на непересекающиеся
классы, называемые связными компонентами.
разбивает
любое множество на непересекающиеся
классы, называемые связными компонентами.
Граф, состоящий из одной связной компоненты, наз-ся связным. Или: граф наз. связным, если любые две его вершины связны.
Деревом называется всякий связный граф, не имеющий циклов.
Изображение графа, в котором никакие 2 ребра не имеют общих точек, кроме их общей вершины, наз. плоским представлением графа. Граф, имеющий плоское представление, наз. плоским. Гранью плоского графа наз-ся максимально связная область на плоскости.
Граф, изоморфный плоскому графу, наз. планарным.
Теорема
Понтрягина – Куратовского:
Граф явл-ся планарным
 он не содержит в качестве подграфа
граф типа1 или граф типа 2(граф, который
можно было сжать до 5- и 6 – угольного
графа).
он не содержит в качестве подграфа
граф типа1 или граф типа 2(граф, который
можно было сжать до 5- и 6 – угольного
графа).
Теорема Эйлера: для любого плоского графа без перегородок справедливо соотношение
 ,
n
- число вершин; m
- число ребер; k-число
граней
,
n
- число вершин; m
- число ребер; k-число
граней
Доказательство:
Пусть дан связный граф G
с n,
m,
k.
Предположим, что этот граф содержит
циклы. Рассмотрим процедуру удаления
ребра, лежащего в цикле. В результате
получим граф
 с
с .
Составим соотношение:
.
Составим соотношение: ,
т.е. соотношение не изменило своей
величины. Если в полученном
,
т.е. соотношение не изменило своей
величины. Если в полученном остались еще циклы, то опять повторяем
описанную процедуру удаления ребра.
При этом
остались еще циклы, то опять повторяем
описанную процедуру удаления ребра.
При этом и т.д. до тех пор, пока не получим граф
без циклов, т.е. дерево
и т.д. до тех пор, пока не получим граф
без циклов, т.е. дерево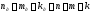 .
.
 (бесконечно-удаленная
грань, т.е. элемент графа). По теореме о
деревьях
(бесконечно-удаленная
грань, т.е. элемент графа). По теореме о
деревьях
 .
.
 чтд.
чтд.