
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
20. Интеграл Лебега и его свойства.
Пусть
функция
 измерима
и огр. На мн-ве
измерима
и огр. На мн-ве и мн- во её знач. Лежит в интервале (А,В).
Разобьём интервал точками
и мн- во её знач. Лежит в интервале (А,В).
Разобьём интервал точками .
. -ранг
разбиения и образ. мн-во
-ранг
разбиения и образ. мн-во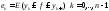 .
Все
.
Все измеримы, попарно не пересекаются и
измеримы, попарно не пересекаются и .
Справедливо равенство:
.
Справедливо равенство: ,
определяются суммы Дарбу-Лебега:
,
определяются суммы Дарбу-Лебега: ,
для них справедливысв-ва
(Дарбу):
,
для них справедливысв-ва
(Дарбу):
При добавлении точек деления нижние суммы не уменьшаются, верхние не увелич-ся.
 3)
3)

Опр.:Интегралом
Лебега от
огранич., измеримой на мн-ве Е функции
 назыв.
общ. знач. точных
назыв.
общ. знач. точных
 границ
верхних и нижних сумм Дарбу-Лебега и
обознач.
границ
верхних и нижних сумм Дарбу-Лебега и
обознач.
 .
.
Интеграл Лебега от измер. Огранич. функции существует всегда.
Св-ва интеграла Лебега:
Если функция огранич.
 ,
тогда
,
тогда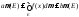 ,
то интеграл Лебега получается тоже
ограниченным.
,
то интеграл Лебега получается тоже
ограниченным.
Док-во:

 ,
, ,
,
 ,
,


f(x)=const. Тогда

μ(E)=0. Тогда
 .
.f(x)>0 Тогда
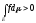 .
(аналогично для <
.
(аналогично для < )
)Счётная аддитивность по мн-ву
 ;
; -не
более чем счётное и они попарно
непересекаются.
-не
более чем счётное и они попарно
непересекаются.
g ~ f
 .
.Конечная аддитивность по функции. Пусть
 и
и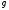 измеримы
на Е, то
измеримы
на Е, то
 -счёт.
аддитивность по функции.
-счёт.
аддитивность по функции.
Однородность интеграла


Док-во:
 ,
,
 ,
,

Если f(x)>=0 на Е и
 0,
тоf
~ 0 на Е
0,
тоf
~ 0 на Е
Предельный переход под знаком интеграла.
Т-ма
Лебега:
Пусть функция
 почти всюду на
почти всюду на сх-ся к
сх-ся к и все
и все огранич.
по модулю одной постоянной
огранич.
по модулю одной постоянной ,
тогда
,
тогда .
.

Сравнение интеграла Лебега с интегралом Римана.
Пусть
функция
 определена
и ограничена на
определена
и ограничена на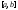 ,
тогда справедлива теорема.
,
тогда справедлива теорема.
Т-ма:
Если
функция интегрируема
на отрезке
интегрируема
на отрезке по Риману, то она интегрируема и по
Лебегу, причём эти интегралы совпадают
по Риману, то она интегрируема и по
Лебегу, причём эти интегралы совпадают . Обратное не верно.
. Обратное не верно.
Восстановление
первообразных для огран. ф-ий: Теорема:
Если ф-ия
f(x)
на отрезке [a,
b]
имеет производную на этом отрезке и
она ограничена, то f(x)=f(a)+
 .
.
Интеграл
Лебега от произ. огран. измеримой ф-ии:
если f(x)
огран на [a,
b],
то срезкой ф-ии f(x)
на [a,
b]
наз.

Срезка
— огранич. и измеримая ф-ия, поэтому
 .
ЕслиN1>N,
то
.
ЕслиN1>N,
то
 .
Если
.
Если ,
то интеграл Лебега возрастает, при этом
послед-ть будет иметь конечный или
беск. предел.
,
то интеграл Лебега возрастает, при этом
послед-ть будет иметь конечный или
беск. предел.
Интегралом
Лебега от неогр., неотриц., произвольной,
измеримой ф-ии на Е, наз конечный или
беск. предел:
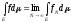 .
Если этот интеграл конечен, то ф-ию наз
суммируемой.
.
Если этот интеграл конечен, то ф-ию наз
суммируемой.
Св-во интеграла Лебега от неогр., неотриц., измерим. ф-ий
Если
 суммируемая.
на Е и
суммируемая.
на Е и
 —суммир.
на Е, то f(x)
суммир. на Е и
—суммир.
на Е, то f(x)
суммир. на Е и

Если f ~ 0, то
 =0.
=0.Если f — суммир. на Е и
 ,
тоcf—суммир.
на Е, т.е.
,
тоcf—суммир.
на Е, т.е.
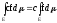 .
.h=f + g, f,g — измеримы на Е, то h суммир, причем
 .
.Теорема Фату: Если послед-ть fn неотриц., измеримых ф-ий на Е почти всюду сходится к f на Е, то
 .
.
Теорема Леви: Послед-ть fn неотриц., неогр., измеримых ф-ий на Е почти всюду сходится к f на Е, не убывает, т.е.
 и
и ,
то
,
то .
.Интеграл Лебега от произ. ф-ии: Пусть f принимает значения на Е разных знаков:
 и
и
f+(x), f—(x) — измеримые и неотриц. ф-ии.
 .
.
Если
хотя бы одна из ф-ий f+(x),
f—(x)
суммир. на Е, то
 .
.
Если обе ф-ии суммируемы, то этот интеграл конечен и f наз. суммируемой на Е.
Св-ва суммир.ф-ий и интегралов:
f суммир.
 |f|
суммируема.
|f|
суммируема.Если
 не пересекаются,f
суммир на Е1,Е2,
тогда f
суммир. на Е и справедливо равенство
не пересекаются,f
суммир на Е1,Е2,
тогда f
суммир. на Е и справедливо равенство
 .
.Если f суммир., то cf — суммир.
 .
.h= f + g —суммир., то h — суммир.

