
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
Обусловленность систем линейных алгебраических уравнений
Прежде
чем говорить о решении задач
 (1), следует убедиться в том, что решение
задачи существует, единственно и
устойчиво. Первые 2 требования будут
выполняться, если определитель матицы
(1), следует убедиться в том, что решение
задачи существует, единственно и
устойчиво. Первые 2 требования будут
выполняться, если определитель матицы .
.
Рассмотрим
выполнение 3-го требования. Входными
данными в задаче будут являться
коэффициенты
 матрицы
матрицы и компоненты вектора
и компоненты вектора .
Они могут задаваться с некоторой
погрешностью
.
Они могут задаваться с некоторой
погрешностью .
Тогда вместо исходной задачи получим
.
Тогда вместо исходной задачи получим .
Чтобы дать оценку погрешности решения
.
Чтобы дать оценку погрешности решения ,
если известны
,
если известны и
и ,
используют понятие нормы.
,
используют понятие нормы.
Существует много способов введения нормы:
 ;
2.
;
2.  ;
3.
;
3. .
.
Самая
распространенная - это Евклидова норма:
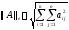 .
.
Справедлива
следующая оценка: (2). Из неравенства (2) видно, что наибольших
изменений в решениях следует ожидать,
когда “велика” матрица, т.е.
(2). Из неравенства (2) видно, что наибольших
изменений в решениях следует ожидать,
когда “велика” матрица, т.е. близка к вырожденной.
близка к вырожденной.
Зависимость
погрешности решения от погрешности
коэффициентов в матрице задается
формулой:

 .
Число
.
Число -
наз. числом обусловленности матрицы
-
наз. числом обусловленности матрицы и обозначается
и обозначается ,
оно зависит от способа введения матричной
нормы.
,
оно зависит от способа введения матричной
нормы.
Матрицы
 ,
для которых число обусловленности
относительно велико наз. плохо
обусловленными, тоже самое говорят о
системе уравнений с матрицей
,
для которых число обусловленности
относительно велико наз. плохо
обусловленными, тоже самое говорят о
системе уравнений с матрицей .
Относительная малость числа обусловленности
говорит о хорошей обусловленности
(систем) матр.
.
Относительная малость числа обусловленности
говорит о хорошей обусловленности
(систем) матр. и соответствующей системы лин. алг.
ур-ний.
и соответствующей системы лин. алг.
ур-ний.
Пусть
 -точное
решение
-точное
решение ,
,
 -
приближенное решение. Существует 2 меры
погрешности решения
-
приближенное решение. Существует 2 меры
погрешности решения вектор ошибки:
вектор ошибки:
1.
 ;
2. Невязка
;
2. Невязка .
.
Вычисление определителей и обращение матриц
Обозначим
определитель системы (1) через D.
 - изменения после первого шага метода
Гаусса.
- изменения после первого шага метода
Гаусса.
 -изменения
после второго шага метода Гаусса.
-изменения
после второго шага метода Гаусса. - изменения послеn-ого
шага.
- изменения послеn-ого
шага.
Следовательно, определитель исходной матрицы
 (4)
(4)
где
 -
ведущие элементы схемы единственного
деления. Т.о. для вычисления определителя
системы нужно получить произведение
ведущих элементов, используемых на
каждом шаге прямого хода метода Гаусса.
-
ведущие элементы схемы единственного
деления. Т.о. для вычисления определителя
системы нужно получить произведение
ведущих элементов, используемых на
каждом шаге прямого хода метода Гаусса.
Схема
единственного деления может использоваться
также и для вычисления элементов
матрицы A-1,
обратной
для невырожденной матрицы
A.
По определению
 ,
гдеЕ
— единичная матрица. Представим искомую
матрицу A-1
и
единичную матрицу в виде совокупности
векторов-столбцов:
,
гдеЕ
— единичная матрица. Представим искомую
матрицу A-1
и
единичную матрицу в виде совокупности
векторов-столбцов:
 (структура
векторов e(i)
предельно проста: i-й
элемент равен единице, а все остальные
— нулю). В такой записи соотношение
(структура
векторов e(i)
предельно проста: i-й
элемент равен единице, а все остальные
— нулю). В такой записи соотношение
 предстанет в виде совокупности изn
систем линейных алгебраических уравнений
вида
предстанет в виде совокупности изn
систем линейных алгебраических уравнений
вида
 (5)
(5)
Решение каждой системы дает соответствующий столбец обратной матрицы.
При нахождении обратной матрицы указанным методом существенно, что все системы, входящие в (5), имеют одинаковую матрицу и фактически могут решаться одновременно.
Итерационные методы
К итерационным методам относятся: метод простых итераций, метод Зейделя, метод релаксации, градиентные методы и их модификации. Итерационные методы применяются для решения систем порядка 106.
 .
При решении
уравнений методом итераций решение
находится как предел последовательности
итерационных приближений. При этом
последовательность может быть сходящейся
или расходящейся. Далее возникает
вопрос о сходимости этой последовательности.
.
При решении
уравнений методом итераций решение
находится как предел последовательности
итерационных приближений. При этом
последовательность может быть сходящейся
или расходящейся. Далее возникает
вопрос о сходимости этой последовательности.
Функции
 ,
определенная в некотором множестве
,
определенная в некотором множестве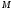 (
( )
наз.метрикой,
если
выполняются условия: 1.
)
наз.метрикой,
если
выполняются условия: 1.  ;
2.
;
2. ;
;
3.
 ; 4.
; 4.
Множество
с введенной на ней метрикой наз.
метрическим
пространством. Полное метрич. пространство,
если в нем любая фундаментальная посл-ть
сходится. Послед-ть
 элементов метрического пространстваX
наз-ся фундаментальной,
если для
элементов метрического пространстваX
наз-ся фундаментальной,
если для

Пусть
 -
отображение, действующее в метрическом
пр-ве
-
отображение, действующее в метрическом
пр-ве с метрикой
с метрикой .
. -
образы элементов
-
образы элементов .
.
Отображение
 пр-ва
пр-ва наз.сжимающим,
если
выполняется условие
наз.сжимающим,
если
выполняется условие
 .
Точка
.
Точка наз. неподвижной точкой отображения
наз. неподвижной точкой отображения ,
если выполняется
,
если выполняется
Принцип
сжимающих отображений (Теорема Банаха):
Сжимающее отображение полного
метрического пространства в себя имеет
единственную неподвижную точку, т.е.
уравнение Fx=x
имеет единственное решение и оно может
быть получено методом простых итераций
 при
любом приближении.
при
любом приближении.
Оценка
расстояния между неподвижной точкой
отображения и некоторым приближением
 задаются формулой:
задаются формулой: получим:
получим: ,
т.о. для решения методом итераций
достаточно установить, что отображение
является сжимающим.
,
т.о. для решения методом итераций
достаточно установить, что отображение
является сжимающим.
Метод простых итераций
Будем решать систему лин.алгебраических уравнений методом простых итераций:
 (1)
(1)
Система (1) имеет единственное решение:
 (2)
(2)


Последнюю систему перепишем: X=CX+D.
Выберем
начальное приближение
 и
построим итерационную последовательность:
и
построим итерационную последовательность:
 .
.
Эта последовательность будет сходиться к решению системы, если отображение F(X)=CX+D будет сжимающим(в силу теоремы Банаха о сжимающем отображении), т.е. если будет выполняться след.неравенство:
 (3).
(3).
Выясним
условия, при которых будет выполняться
нер-во(3). В качестве метрики
 можно вывбрать след.норму:
можно вывбрать след.норму:
Отметим,
что нер-во(3) примет вид:
 (4).
(4).
По
свойствам нормы справедливо:
 (5).
(5).
Сравнивая
нер-ва (5) и (4) можно сделать вывод, что
отображение F
будет сжимающим, если
 .
Из теоремы Банаха следует, что оценка
погрешности может определяться
равенством:
.
Из теоремы Банаха следует, что оценка
погрешности может определяться
равенством:

Метод Зейделя
Этот
метод является модификацией метода
простых итераций. Отличие от метода
простых итераций заключается в том,
что на каждом шаге итерационного
процесса при вычислении
 используются уже найденные значения
используются уже найденные значения

Достаточное
условие сходимости метода Зейделя:
норма матрицы приводимой к итерационному
виду должна быть меньше 1, т.е.
 Этот метод обеспечивает более быструю
сходимость, чем метод простых итераций.
Этот метод обеспечивает более быструю
сходимость, чем метод простых итераций.
