41. Маршруты в графах и деревья

Графом называется совокупность множеств вершин A и ребер U : .

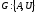Ребрами графа наз-ся отрезки, концами которых явл-ся вершины.

Чередующаяся последовательность вершин и ребер, где каждое ребро имеет вид 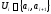наз-сямаршрутом. Длиной маршрута называется число ребер данного маршрута.

Начало маршрута определяет начальную вершину, конец - конечную, а остальные - промежуточ­ные.

Цепью называется такой маршрут, в котором все ребра различны (каждое ребро не встречается более одного раза).

Цепь называется простой, если каждая вершина встречается ровно один раз (маршрут, в котором все ребра и все вершины различны).

Циклическим маршрутом наз-ся маршрут, соединяющий вершину саму с собой ( начало и конец у такого маршрута совпадают).

Циклическая цепь наз-ся циклом (циклический маршрут, в котором все ребра различны).

Циклическая простая цепь наз-ся простым циклом, т.е. циклический маршрут, в котором все ребра и вершины не совпадают.

Эйлеровой цепью наз-ся цепь, содержащая все ребра графа (не более 1 раза).

Эйлеровым циклом наз-ся цикл, содержащий все ребра графа.

Граф, содержащий эйлеров цикл наз-ся эйлеровым графом.

В качестве критерия эйлеровости выступает теорема: граф G является эйлеровымграф связный и все ребра в вершинах возникают парами, т.е.степени всех вершин четные.

Граф G явл-ся полуэйлеровымон содержит эйлерову цепь. Необходимые и достаточне условия полуэйлеровости: граф G является полуэйлеровымграф связный и содержит ровно две нечетные вершины.

Всякую замкнутую линию, если её можно начертить не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз называют уникурсалъной. Рисунок эйлерова или полуэйлерова графа, наз-ся уникурсальной линией.

Замкнутую фигуру в которой все вершины четны можно начертить одним росчерком, начиная обводить с любой точки или вершины.

Замечание: От эйлеровой цепи всегда можно перейти к эйлерову циклу, добавив ровно одно ребро, которое должно соединять две нечетные вершины. И наоборот, если дан эйлеров цикл, то удалив любое ребро графа получим эйлерову цепь. Построение эйлеровой цепи нужно начинать в одной нечетной вершине и заканчивать в другой.

Гамильтоновой цепью (циклом) наз-ся цепь (цикл), содержащая все вершины ровно по одному разу, Гамильтоновые цепь и цикл соответственно явл-ся простой цепью и циклом.

Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Достаточные условия существования гамилътоновых циклов:

1) Всякий полный граф является гамильтоновым. (У полного графа любые две вершины смежны).

2) Если граф помимо простого цикла содержит и другие ребра, то он также является гамиль­тоновым.

3) Если для любой пары вершин графа с п вершинами сумма их степеней не меньше п. то граф обладает гамильтоновым циклом.

4) Граф с n вершинами имеет гамильтоновый цикл, если для каждой его вершины степень больше или равна n/2.

Деревом называется всякий связный граф, не имеющий цикла.

Из определения следует, что дерево не содержит петель и кратных ребер, и для каждой пары вершин существует единственный путь, соединяющий их. Принято считать, что граф, состоящий из одной изолированной вершины, также является деревом.

Расстоянием между вершинами a и b графа наз-ся количество ребер в соединяющей их простой цепи r(a,b).

Для каждой вершины дерева G определим 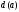- расстояние от вершиныa до максимально от нее удаленной вершины: .

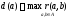Наименьшее из всех 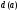наз-сярадиусом дерева:,а максимальное –диаметром дерева: .

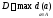Те вершины дерева, на которых достигается 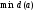наз-сяцентральными вершинами или центром дерева. Любое дерево имеет либо один, либо два центра. Если у дерева два центра, то центральные вершины явл-ся смежными.

Вершины дерева, степень которых равна 1, наз-ся концевыми или висячими. Любое дерево с имеет по крайней мере две висячих вершины. Для любой вершиныa дерева G величина 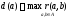реализуется на концевых вершинах.

Первоначально выбранная вершина называется корнем дерева.

Всякое ребро в дереве явл-ся мостом, т.е. его удаление нарушает связность. Лесом наз-ся несвязный граф без циклов, причем каждая связная компонента такого графа явл-ся деревом. Лес, состоящий из k деревьев и имеющий п вершин содержит (n — k) ребер.

Алгоритм для определения центральных вершин.

Пусть G – исходное дерево. Удалим из графа все концевые вершины с инцидентными к ним ребрами. Получим граф , который также явл-ся деревом, причем центральные вершины графовG и совпадают, радиус графа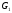уменьшается на 1, а диаметр – на 2. Если в полученном графеимеются еще концевые вершины с инцидентными ребрами, то будем продолжать процесс удаления далее, пока это возможно. В результате получим дерево, состоящее из одной вершины либо из двух смежных вершин. Причем эти оставшиеся вершины явл-ся центральными вершинами исходного графа. Радиус и диаметр дерева связаны следующими соотношениями:

Основная теореа о деревьях.

Дан граф G с п вершинами, m ребрами. Эквивалентны следующие условия:

1. граф G – дерево;

2. G – граф без циклов, ;

3. G – граф связный, ;

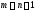4. граф G –связный, каждое его ребро явл-ся мостом;

5. любые две вершины этого графа соединимы единственной простой цепью;

6. граф G не содержит циклов, и добавление к нему произвольного ребра приводит к образованию ровно одного простого цикла.

Замечание: для любого графа выполняется неравенство 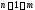, а в дереве это неравенство превращается в равенство, что говорит о том, что дерево – это граф с минимальным количеством ребер(об этом свидетельствует условие 4).

Докажем эквивалентность некоторых утверждений теоремы.

Док-во того, что из условия :

Пусть дано дерево G с п вершинами, m ребрами. Покажем, что граф G явл-ся связным графом, в котором каждое ребро – мост. Предположим, что это неверно, и в графе существует какое-либо ребро U, соединяющее вершины a и b 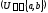,которое мостом не явл-ся. Удалим из графа G ребро U, получим граф 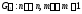. Причем граф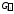не связный, т.к. удалили не мост.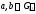, т.к.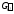- связный, тоa и b – связные вершины.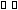цепь, их соединяющая. Таким образом, в исходном графе G получается простой цикл, что противоречит тому, что G –дерево.предположение неверно, значит, каждое ребро дереваG –мост .чтд.

Док-во того, что из условия :

Пусть граф G без циклов и выполняется равенство 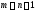. Покажем, что графG – связный граф. Предположим, что граф G связным не явл-ся. Тогда 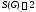(как минимум имеет две связные компоненты). Пусть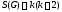, т.е. компонентысвязные компоненты графаG. Рассмотрим каждую компоненту по отдельности.

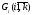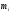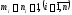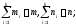
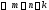Каждый граф - дерево, в котором вершин иребер. В каждом таком дереве по условию 2 выполняется равенство. Просуммируем полученные соотношения по всем индексамi: т.к., где. А это неверно, т.к. в исходном графе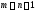предположение неверно, и графG явл-ся связным.Чтд.

Док-во того, что из условия :

Пусть граф G –связный, . Покажем, что любое ребро в графе явл-ся мостом. Предположим, что в графе найдется реброU- не мост. Удалим это ребро из графа G.Получим граф 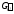- связный.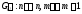. Т.к. граф- связный, то для него выполняется неравенство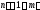(т.к.и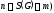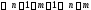, что противоречит условию.предположение неверно, и любое ребро явл-ся мостом. Чтд.