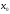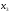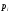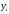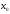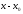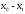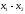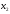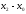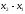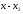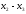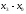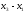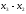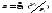- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
27. Численное дифференцирование. Численное интегрирование
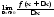
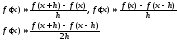
Применение ряда Тейлора для численного дифференцирования
Разложим f(x+h) в ряд Тейлора, h- мало
 (1)
(1)
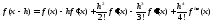 (2)
(2)
(1)-(2)
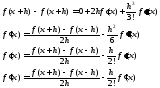
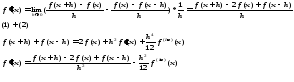
Интерполяционные формулы Ньютона:
Часто
интерполирование ведется для функций,
заданных таблицами с равноотстоящими
значениями аргумента. В этом случаи
шаг таблицы
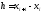 (i=0,1,2,…)
является величиной постоянной. Для
таких таблиц построение интерполяционных
формул упрощается.
(i=0,1,2,…)
является величиной постоянной. Для
таких таблиц построение интерполяционных
формул упрощается.
Пусть функция задана таблицей с постоянным шагом. Разности между значениями функции в соседних узлах интерполяции – конечные разности первого порядка
 (i=0,1,2,…).
(i=0,1,2,…).
Из конечных рахностей первого порядка образуются конечные разности второго порядка:
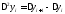 (i=0,1,2,…).
(i=0,1,2,…).
Конечные разности любого порядка могут быть представлены через значения функции
 .
.
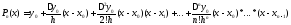
Пусть
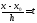 .
Тогда
.
Тогда
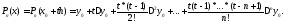 (1)
(1)
Эта формула применяется для интерполирования в начале отрезка интерполяции, когда t мало по абсолютной величине.
Когда значение аргумента находится ближе к концу отрезка интерполяции, применяют следующую формулу Ньютона:
 (2)
(2)
Интерполяционный многочлен Лагража
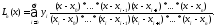
Используя
обозначение
 ,
формуле Лагранжа можно придать более
сжатый вид
,
формуле Лагранжа можно придать более
сжатый вид
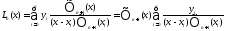
Применение формулы Лагранжа приводит к большому числу однотипных вычислений. Организация вычислений улучшится , если пользоваться специальной схемой.
В таблице показано построение такой схемы для 4 узлов (i=0,1,2,3). Таблица составляется заново для каждого аргумента х.
Заполнение таблицы начинается с того, что вычисляются и заносятся в соответствующие клетки все элементарные разности. Затем вычисляются произведения р разностей по строкам.
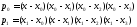
|
.x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 -
знаменатель в формуле Лагранжа.
-
знаменатель в формуле Лагранжа.
Численное интегрирование
На практике в редких случаях удаются точно вычислить интеграл или проинтегрировать обыкновенное диф. уравнение.
В элементарных функциях не вычисляются некоторые интегралы и не интегрируются некоторые уравнения. Тем более невозможно точно найти интеграл, если функция задана таблицей или графиком. В этом случаи используют приближенные методы интегрирования. Формулы для приближенного вычисления однократных интегралов – квадратурные формулы.
 ,
f(x)
– непрерывна на [a,b]
,
f(x)
– непрерывна на [a,b]
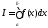 -
квадратурная, если справедливо
-
квадратурная, если справедливо
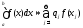 .
.
 -
число ,
-
число ,
 - веса квадратурной формулы,
- веса квадратурной формулы,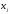 - точки из [a,b]
,
- точки из [a,b]
,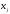 -
узлы квадратурной формулы
-
узлы квадратурной формулы
Формула прямоугольников:
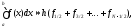 N-
количество интервалов разбиения(частичных
отрезков),
N-
количество интервалов разбиения(частичных
отрезков),
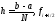 - значениеf
в середине частичного отрезка.
- значениеf
в середине частичного отрезка.
Формула трапеций:
 N-
кол-во интервалов разбиения(частичных
отрезков),
N-
кол-во интервалов разбиения(частичных
отрезков),
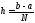 .
.
Формула Симпсона:
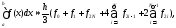 2N-
кол-во интервалов разбиения(частичных
отрезков),
2N-
кол-во интервалов разбиения(частичных
отрезков),
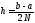 .
.