
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
Обыкновенным
дифференциальным уравнением (ду) явл-ся
уравнение первого порядка
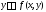 [1], где
[1], где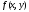 -
заданная непрерывная функция в области
-
заданная непрерывная функция в области
 .
Основная задача, связанная с этим
уравнением, известна как задача Коши:
найти решение уравнения [1] в виде функции
.
Основная задача, связанная с этим
уравнением, известна как задача Коши:
найти решение уравнения [1] в виде функции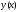 ,
удовлетворяющей начальному условию
,
удовлетворяющей начальному условию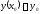
 .
Геометрически это означает, что требуется
найти интегральную кривую
.
Геометрически это означает, что требуется
найти интегральную кривую ,
проходящую
через заданную точку
,
проходящую
через заданную точку
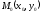 при выполнении равенства[1].
В силу теоремы Пеано задача Коши [1]-
при выполнении равенства[1].
В силу теоремы Пеано задача Коши [1]-
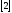 имеет решение на некотором отрезке
имеет решение на некотором отрезке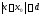 .
Если же функция
.
Если же функция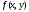 удовлетворяет условию Липшица по
удовлетворяет условию Липшица по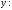
 ,
то задача Коши [1]-
,
то задача Коши [1]-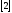 имеет единственное решение на отрезке
имеет единственное решение на отрезке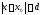 .
Если область
.
Если область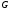 вместе с любыми точками
вместе с любыми точками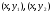 содержит отрезок, их соединяющий, а
функция
содержит отрезок, их соединяющий, а
функция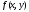 имеет ограниченную производную
имеет ограниченную производную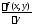 ,
то
,
то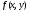 удовлетворяет
условию Липшица. При этом
удовлетворяет
условию Липшица. При этом .
Пусть
.
Пусть -
прямоугольник
-
прямоугольник ,
содержащийся в
,
содержащийся в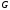 .
В силу непрерывности функция
.
В силу непрерывности функция ограничена
ограничена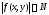 .
. задача Коши [1]-
задача Коши [1]-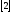 имеет единственное решение на отрезке
имеет единственное решение на отрезке ,
где за
,
где за можно выбрать любое положительное
число, удовлетворяющее условию
можно выбрать любое положительное
число, удовлетворяющее условию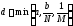 .
.
Метод Эйлера
В основе метода ломаных Эйлера лежит идея графического построения решения ду, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.
Пусть
дано уравнение
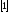 с начальным условием
с начальным условием .
Выбрав достаточно малый шаг
.
Выбрав достаточно малый шаг ,
построим, начиная с точки
,
построим, начиная с точки систему равноотстоящих точек
систему равноотстоящих точек .
Вместо искомой интегральной кривой на
отрезке
.
Вместо искомой интегральной кривой на
отрезке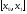 рассмотрим отрезок касательной к ней
в точке
рассмотрим отрезок касательной к ней
в точке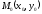 (обозначим ее
(обозначим ее с уравнением
с уравнением ).
).
При
 из уравнения касательной
из уравнения касательной ,
откуда видно, что приращение значения
функции на первом шаге имеет вид:
,
откуда видно, что приращение значения
функции на первом шаге имеет вид: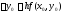 .
Аналогично, проводя касательную
.
Аналогично, проводя касательную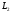 к некоторой интегральной кривой
семейства в точке
к некоторой интегральной кривой
семейства в точке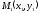 ,
получим:
,
получим: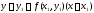 ,
что при
,
что при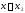 дает
дает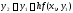 ,
т.е.
,
т.е. получается из
получается из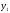 добавлением приращения
добавлением приращения .
.
Таким
образом, получение таблицы значений
искомой функции
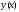 по методу Эйлера заключается в
циклическом применении пары формул
по методу Эйлера заключается в
циклическом применении пары формул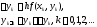
Метод
Эйлера обладает малой точностью, к тому
же погрешность каждого нового шага
систематически возрастает. Наиболее
приемлемым для практики методом оценки
точности является в данном случае
способ двойного счета – с шагом
 и с шагом
и с шагом .
Совпадение десятичных знаков в полученных
двумя способами результатах дает
естественные основания считать их
верными.
.
Совпадение десятичных знаков в полученных
двумя способами результатах дает
естественные основания считать их
верными.
Метод Эйлера-Коши
Существуют
различные уточнения метода Эйлера,
повышающие его точность. Модификации
метода обычно направлены на то, чтобы
более точно определить направление
перехода из точки
 в точку
в точку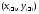 .
Метод Эйлера-Коши, например, рекомендует
следующий порядок вычислений:
.
Метод Эйлера-Коши, например, рекомендует
следующий порядок вычислений:
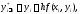
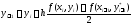 .
.
Геометрически
это означает, что мы определяем
направление интегральной кривой в
исходной точке
 и во вспомогательной точке
и во вспомогательной точке ,
а в качестве окончательного берем
среднее этих направлений.
,
а в качестве окончательного берем
среднее этих направлений.
Методы Эйлера и Эйлера-Коши явл-ся методами Рунге-Кутты 1-2 порядка.
Метод Рунге-Кутта.На практике наиболее распространенным являетсяметод Рунге-Кутта4го порядка. Расчетные формулы этого метода имеют вид:
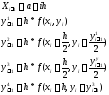
Итоговое
значение получается по формуле

Метод конечных разностей
Краевая
задача для линейного ду

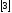 ,
где
,
где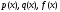 - некоторые непрерывные на
- некоторые непрерывные на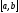 функции, состоит в нахождении его
решения
функции, состоит в нахождении его
решения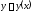 ,
удовлетворяющего двухточечным линейным
краевым условиям:
,
удовлетворяющего двухточечным линейным
краевым условиям: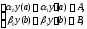
 ,
где
,
где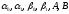 - постоянные и
- постоянные и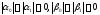 .
.
При
решении этой задачи методом конечных
разностей отрезок
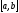 разбивается на
разбивается на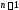 частей с шагом
частей с шагом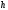 ,
где
,
где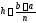 .
.
Точки
разбиения имеют абсциссы
 .
.
Значения
в точках деления
 искомой функции и ее производных
искомой функции и ее производных обозначим соответственно через
обозначим соответственно через .
.
Заменяя
производные правыми односторонними
конечноразностными отношениями для
внутренних точек
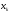 отрезка
отрезка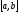 ,
приближенно будем иметь
,
приближенно будем иметь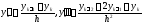
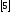 .
.
Для
концевых точек
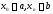 полагаем
полагаем и
и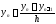
 .
.
Используя
формулы
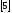 ,
ду
,
ду при
при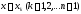 приближенно можно заменить линейной
системой уравнений
приближенно можно заменить линейной
системой уравнений![]() .
.
Кроме
того, в силу формулы
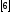 краевые условия
краевые условия дополнительно дают еще два уравнения
дополнительно дают еще два уравнения
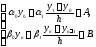
Т.о.,
получена линейная система
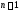 уравнений с
уравнений с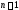 неизвестными
неизвестными ,
представляющими собой значения искомой
функции
,
представляющими собой значения искомой
функции .
.

Обозначим
 .
После алгебраических преобразований
система примет вид
.
После алгебраических преобразований
система примет вид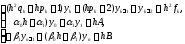
Решив
систему, получим таблицу значений
искомой функции
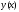 .
.
Аппроксимация функций
Из курса математики известны 3 способа задания функциональных зависимостей:
1) аналитический
2) графический
3) табличный
Табличный способ обычно возникает в результате эксперимента.
Недостаток табличного задания функции заключается в том, что найдутся значения переменных, которые неопределенны таблицей. Для отыскания таких значений определяют приближающую к заданной функцию, называемую аппроксимирующей, а действие замены - аппроксимацией.
Аппроксимация
заключается в том, что, используя
имеющуюся информацию по
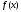 ,
можно рассмотреть другую функцию
,
можно рассмотреть другую функцию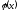 ,
близкую в некотором смысле к
,
близкую в некотором смысле к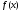 ,
позволяющую выполнить над ней
соответствующие операции и получить
оценку погрешности такой замены. Тогда
,
позволяющую выполнить над ней
соответствующие операции и получить
оценку погрешности такой замены. Тогда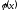 - аппроксимирующая функция.
- аппроксимирующая функция.
Интерполяция
явл-ся частным случаем аппроксимации.
Если требуется получить значение
функции
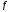 для такого значения аргумента
для такого значения аргумента
 ,
который входит в отрезок
,
который входит в отрезок ,
но не совпадает ни с одним из значений
,
но не совпадает ни с одним из значений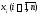 ,
то такая задача наз-сяинтерполяцией
–
приближенное вычисление значений
функций в промежутках между узловыми
точками.
,
то такая задача наз-сяинтерполяцией
–
приближенное вычисление значений
функций в промежутках между узловыми
точками.
При
интерполяции требуется совпадение
значений исходной и приближающей
функции в узлах интерполяции, т.е. в
точках
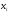 .
При аппроксимации функции совпадение
значения исходной и приближающей
функций не требуется.
.
При аппроксимации функции совпадение
значения исходной и приближающей
функций не требуется.
Классический
подход к решению задачи построения
аппроксимирующей функции основывается
на требовании строгого совпадения
исходного и приближенного значений
функций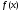 и
и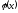 в точках
в точках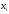 ,
т.е.
,
т.е.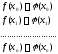 .
Будем искать функцию в следующем виде:
.
Будем искать функцию в следующем виде: .
Получаем систему алгебраических
уравнений с неизвестными
.
Получаем систему алгебраических
уравнений с неизвестными .
Система всегда имеет единственное
решение, т.к. определитель не равен
0.чаем
систему алгебраических уравнений с
неизвестными значений фуй функций не
требуется.
.
Система всегда имеет единственное
решение, т.к. определитель не равен
0.чаем
систему алгебраических уравнений с
неизвестными значений фуй функций не
требуется.
 интерполяционный
многочлен
интерполяционный
многочлен
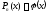 для функции
для функции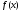 ,
заданной таблично, имеет степень не
большую
,
заданной таблично, имеет степень не
большую .
.
Для
определения коэффициентов применяют
интерполяционные многочлены специального
вида, к ним относится и многочлен
Лагранжа
 ,
который имеет вид
,
который имеет вид ,
где
,
где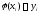 .
В точках отличных от узлов интерполяции
полином Лагранжа в общем случае не
совпадает с заданной функцией.
.
В точках отличных от узлов интерполяции
полином Лагранжа в общем случае не
совпадает с заданной функцией.
