21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.

Функции комплексной переменной. 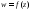. Отображение f , z- некоторое комплексное число z = x + iy ,w=U+iV. Функцией компл. переменной наз отображение, при кот. каждому элементу z соотв. один и только один элемент w.

Предел функции. Опр:

Т-ма: f(z)=U(x,y)+V(x,y) имеет конечный предел в точке x₀+iy₀ тогда и т. т. когда ее действ. и мнимая части имеют предел в этой точке, причем предел действ-ой части равен действ-ой части предела (предел мнимой части равен мнимой части предела).

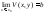
Опр: Функция f(z) назыв-ся непр-ой в т.z=a если (a- неизолиров. т).

Если а - изолированная точка, то ф-ция в ней считается непр-й по опред-ю. Ф-ция f(z) непрерывна на мн-ве D, если она непрерывна в каждой его точке.

Т-ма: f(z) = U(x,y)+iV(x,y) непрерывна в точке (x₀,y₀), когда в этой точке непрерывны ф-ции U(x,y) и V(x,y).

Т-ма: Если f, g непрерывны в т.z₀, то в этой точке непрерывны их сумма, разность, произведение, частное, а также сложная ф-ия h(z)=g(f(z)).

Опр: однозначная ф-я назыв. аналитической в некот. обл-ти, если в любой точке этой обл. она имеет производную.

Ф-ия наз. гармонической, если она уд. ур-ию Лапласа:

Если U+iV — аналитическая, то U и V — сопряжено гармонич.

Условия Коши - Римана. Для того чтобы ф-ция f(x)=U(x,y)+iV(x,y) была диф-мой (имела производную) в точке z=x+iy н.и д. чтобы в этой точке были диф-мы ф-ции U(x,y) и V(x,y) и выполнялось условие:

и при этом.

Док-во: Необх: Пусть ,=

1) ,

=

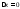2) ,

=.

при

при .Достаточность: дано ,, ф-цииU и V- дифференцируемы в точке (x,y). Надо док-ть что , гдеz=x+iy.

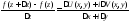
- определение дифференцируемости.

,

,,,

, т.к. = конечному числупроизводная существует.ч.т.д.

Элементарные функции:

1.

Линейная функция. w=az+b. 1) w=z+c – это преобразование переноса на вектор c.

2) - это преобразование вращения, т.е это поворот относительно начала координат на угол. 3)w=kz, - преобразование подобия.

Дробно-линейная ф-ция., ,ad=bc, ,

, если c=0 .-линейные преобразования – это часть дробно-линейных преобразований.

Логарифмическая и показательная ф-ия. ln z — число w, что e^w=z; ln z-многозначная ф-ия.

w=ln z=ln r+i(φ+2πk), k, — модуль компл. числа, φ =Arg z+2πk — аргумент компл. числа; - π φπ.

В отличие от лог. действ. числа, можно считать лог. отриц. чисел.

Св-ва: 1) , 2)3). Д-во:

.

Показательная ф-ия: w=e^z. Св-ва: 3) Периодом показ. ф-ии явл.T=2πki 4) Нули ф-ии: нулей нет: ;cos y=0 и sin y=0. Но одновр. эти ф-ии не могут иметь одинак. решения.

1) Все периоды кратны 2πk 2) нули ;

Степенная ф-ия:

1)

2)

Для рац. b имеется q различн. значений.

Производные элем. ф-ий:

Интегрирование: Определение интеграла: пусть задана некот. кривая С, на кот. определено направление и в каждой ее точке опред. некот. ф-ия f(z)

. Если сумма σ имеет конечный предел, не завис. от выбора точек 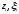, при том, что все разности, то этот предел наз. интегралом ф-ииf(z) по кривой С

.

Кривая наз. гладкой, если она задается параметр. ур-иями , где эти ф-ии непрерывно диффер. и их производные не обращ в ноль одновременно.

Кривая наз. кусочно-гладкой, если она состоит из конечного числа гладких частей.

Вычисление интеграла:

Св-ва интеграла: (получ. из св-в криволин. интеграла)

1) — ф-ииf и g непреравны на кусочно-гладких кривых.

2)

3)

4) — длина кривой С

5) — кривая С, кот. обходится в обратном направлении.

Интегральная теорема Коши (для односвязной области): интеграл по замкн. кривой С равен 0, если кривая ограничивает область D и подынтегр. ф-ия аналитическая не только в области D, но и в нек. области, содерж. обл-ть D вместе с границей. Д-ВО: ,

f(z) — аналитическая, т.е. и. Тогда

Интегральная теорема Коши (для многосвязной области): Если область D ограничена конечным числом кусочно-гладких кривых, а ф-ия f(z)— аналитическая внутри области, содерж. обл-ть D и ограничивающей ее кривые, то интеграл по внешнему контуру равен сумме интегралов по внутр. контуру.(все контуры обходятся против час. стрелки).

Интегральная ф-ла Коши: Если замкнутая кривая С огранич. односвязн. область D, а f(z) — аналитическая в D, содерж. обл-ть D и границу С, то для всякой внутр. точки z обл-ти D справедл. ф-ла: