Достаточное условие сходимости итерационного процесса

Рассмотрим условия, при которых отображение будет сжимающим. Из определения, что это зависит от способа метризации пространства.

Пусть - 2 точки-мерного пространства.

На практике удобно рассматривать систему лин. алг. ур-ний в пространстве с одной из следующих метрик:

1. ; 2.; 3.

Поэтому, чтобы отображение заданное на метрическом пространстве было сжимающим достаточно выполнение одного из следующих условий:

1. Пространство с метрикой :

2. Пространство с метрикой :

3. Пространство с метрикой :

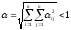
25. Решение нелинейных уравнений и систем уравнений

Метод простой итерации. Заменим уравнение F(x)=0 равносильным ему уравнением x=f(x) (2). Выберем х₀-начальное приближение. Применяя шаг за шагом соотношение x_n=f(x_n-1) для n=1,2,…, образуем числовую последовательность х₀,х₁,…,x_n,… (3), которую называют последовательностью приближений или итерационной последовательностью, которая может быть сходящейся или расходящейся.

Достаточные условия сходимости.

Пусть уравнение x=f(x) имеет единственный корень на отрезке [a,b] и выполнены условия: 1)f(x) определена и дифференцируема на [a,b]; 2) f(x) принадлежит [a,b] для всех х принадлежит [a,b]; 3) существует такое вещественное q, что | f `(x)|≤q<1 для всех принадлежащих [a,b]. Тогда итерационная последовательность сходится при любом начальном приближении х₀ принадлежащем [a,b].Если последовательность (3) сходится, а функция f(x)непрерывна, то предел этой последовательности является корнем уравнения (2). х^*=lim x_n, x_n=f(x_n-1); х^*=lim x_n=lim f(x_n-1)=f(lim x_n-1)=f(х^*);х^*= f(х^*).

На практике итерационная последовательность не может продолжаться бесконечно, поэтому приходиться обрывать процесс при этом возникает погрешность метода итераций, которая определяется неравенством . Если результат должен быть получен с точностью ε, то получим неравенство(чем меньше значениеq, тем быстрее сходиться итерационная последовательность). Значит для нахождения корня уравнения x=f(x) методом итераций с точностью ε, нужно продолжать итерации до тех пор, пока модуль разности между последними соседними приближениями остается больше числа .

Уравнение F(x)=0 может быть приведено к виду x=f(x) многими способами, однако это требуется сделать так, чтобы для функции f(x) выполнялись Д условия сходимости. Следует иметь ввиду следующие специальные приемы:

1. Уравнение F(x)=0 преобразуем к виду x=x-mF(x), где m=const≠0. В этом случае можно принять f(x)=x-mF(x). Дифференцируя, получим f `(x)=1-m F `(x). Для того, чтобы было |f `(x)|=|1- m F `(x)| ≤q<1, достаточно подобрать m так (если это возможно), чтобы для всех х отрезка [a,b] выполнялось неравенство 0<p≤ m F `(x) ≤1 (m может быть разным, главное чтобы выполнялись условия сходимости);

2. Пусть уравнение F(x)=0 записано в виде x=f(x), однако при исследовании функции f(x) на отрезке [a,b] оказалось, что для всех х из этого отрезка |f `(x)|>1. Тогда вместо функции y=f(x) рассмотрим функцию x=g(y), обратную для f(x). Будем решать теперь уравнение y =g(y) (или в старых обозначениях, х=g(х)). По свойству производных обратных функций теперь на отрезке [a,b] |g `(x)|=<1, так что для уравнения х=g(х), равносильного исходному, условие 3) оказывается выполненным.

Метод Ньютона (метод касательных)

y=F(x₀)+F `(x<sub>0</sub>)(x-x<sub>0</sub>); ∩ OX: y=0; F(x<sub>0</sub>)+F `(x₀)(x-x₀)=0

x=;x_n=- итерационная формула нахождения корней.

Погрешность ∆х_n=|x_n-x^*|≤, гдеm=min|F `(x)| на отрезке [a,b].

Модифицированный метод Ньютона используется в случае, когда производную ф-и F′ (x) вычислить сложно.

x_n=.

Погрешность ∆х_n=|x_n-x^*|≤, гдеm=min|F `(x)| на отрезке [a,b].

Связь между методом итераций и методом Ньютона.

Метод Ньютона - частный случай метода итераций, когда f(x_n-1)=x_n-1-.

Дост. условие сходимости метода Ньютона можно получить из Дост. условия сходимости метода итераций ,

Достоинства метода Ньютона:

1)очень быстрая сходимость

2)возможность обобщения на случай системы уравнений

Недостатки метода Ньютона:

1)метод Ньютона расходится в тех областях, где F’(x) близко к нулю.

2)требуется вычисление производной в каждом шаге итерационного процесса.

Метод секущих (метод хорд)

Проводится прямая через точки (x0, F(x0)),(x1, F(x1)).

В этом методе приближенное значение х_n вычисляется на основе двух предыдущих значений х_n-1, х_n-2 .

Уравнение прямой ;

Найдем точку пересечения с прямой: F(x)=0; тогда

;

Особенности:

1. не требуется вычисление производной, что приводит к уменьшению объема вычислений,

2. метод является двух шаговым,

3. в знаменателе стоит F(x_n-1)-F(x_n-2), поэтому если F(x_n-1) и F(x_n-2) имеют близкие значении, то это может привести к заметным погрешностям в вычислении,

4. условия сходимости аналогичны усл. сх-ти метода Ньютона.

Погрешность ∆х_n=|x_n-x^*|≤, гдеm=min|F `(x)| на отрезке [a,b].

Решение систем нелинейных уравнений

; Перепишем эту систему в виде F(x)=0, где .

Метод простой итерации

Преобразуем исходную систему к итерационному виду

; Выбираем начальное приближение: ,x^k+1=F(x^k).

Решение находится как предел последовательных приближений. Д условие сходимости метода простых итераций.

Рассмотрим матрицу:

.

Отображение φ будет сжимающим, если sup||φ`(x)||<1, то метод простых итераций сходится к решению системы. Из теоремы Банаха вытекает, что оценка погрешности может опр-ся след.равенством:

,

Метод Ньютона

F(x)=0; X_i+1=x_i-. Для системы нелинейных уравнений:X_i+1=x_i-[φ `(x_i)]^-1.F(x_i)

Модифицированный метод Ньютона

X_i+1=x_i-[φ `(x₀)]^-1.F(x_i)