
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
35. Устойчивость решений дифференциальных уравнений
Устойчивость решений по Ляпунову
Пусть
дана система обыкновенных дифференциальных
уравнений (ОДУ):

(i
= 1…n).
,
где y
– вектор с координатами (y1,…,yn),
y
= (y1,…,yn),
f
= (f1,…,fn).
Норма:
 Пусть начальные данные задаются приx
= x0.
Пусть начальные данные задаются приx
= x0.
Опр:
решение
y
= y0(x)
системы (1) называется устойчивым
по Ляпунову,
при
 ,
если
,
если >
0
>
0 ,x
≥ x0
для любого решения этой системы.
,x
≥ x0
для любого решения этой системы.
||
y(x)
– y0(x)||
< при
||y(x0)–
y0(x0)|
<
при
||y(x0)–
y0(x0)|
< .
.
Если,
кроме того,
 при достаточно малых ||y(x)
– y0(x)||,
то решение
(2) называется асимптотически
устойчивым при
при достаточно малых ||y(x)
– y0(x)||,
то решение
(2) называется асимптотически
устойчивым при
 .
При этом предполагается, что функцияy0(x)
определяется для всех x
≥ x0,
а система (1) определена в некоторой
окрестности y
= y0(x),
вида: || y(x)
– y0(x)||
< M
при x
≥ x0.
.
При этом предполагается, что функцияy0(x)
определяется для всех x
≥ x0,
а система (1) определена в некоторой
окрестности y
= y0(x),
вида: || y(x)
– y0(x)||
< M
при x
≥ x0.
Очевидно,
всегда можно рассматривать случай
y0(x) 0,
взяв вместоy(x)
новую неизвестную функцию y(x)
– y0(x).
Функции fi,
yi
и х считаются действительными.
0,
взяв вместоy(x)
новую неизвестную функцию y(x)
– y0(x).
Функции fi,
yi
и х считаются действительными.
Устойчивость
означает, что малые изменения начальных
условий приводят к малому отличию
решений при x
≥ x0,
а асимптотическая устойчивость означает,
что при малом отличии начальных данных,
решения неограниченно приближаются к
y0(x)
при
 .
.
Пример
1: Рассмотрим
уравнение
 ,y
= c
– решение. Начальное условие: y(x0)
= 0, y
= 0. Будет ли это решение устойчивым?
,y
= c
– решение. Начальное условие: y(x0)
= 0, y
= 0. Будет ли это решение устойчивым?

Решение y = y0 устойчиво, но асимптотической устойчивости нет.


Пример 2: (a = const, a ≠ 0). Начальное условие: y(x0) = y0.
 Решение:
Решение:
 y(x0)
= 0, y
= 0.
y(x0)
= 0, y
= 0.

 Решение
устойчиво асимптотически.
Решение
устойчиво асимптотически.







Пример
3: x(t) 0x(t0)
0x(t0) 0.
0.
Решение
неустойчиво при


Действительно,
общее решение имеет вид:
При t,
x0≠0:
x(t)|
 Следовательно, при достаточно больших
Следовательно, при достаточно больших
t
> t0
неравенство |x(t)
- 0| <
 не
выполняется.x(t)
не
выполняется.x(t) 0
– неустойчивое решение.
0
– неустойчивое решение.
При исследовании устойчивости и асимптотической устойчивости важную роль играет теорема Ляпунова.
Теорема Ляпунова об устойчивости и асимптотической устойчивости:
Пусть
для некоторого
 > 0 правая часть системы (1)определена
и непрерывна при
> 0 правая часть системы (1)определена
и непрерывна при и ||y
|| <
и ||y
|| <
 иf(x,
0)
иf(x,
0) 0.
Пусть при тех же значенияхy
существует непрерывно дифференцируемая
«функция Ляпунова»: V(y)
≥ 0 и равна нулю лишь в начале координат.
0.
Пусть при тех же значенияхy
существует непрерывно дифференцируемая
«функция Ляпунова»: V(y)
≥ 0 и равна нулю лишь в начале координат.
а)
Если

 то нулевое решениеy(x)
то нулевое решениеy(x)
 0 системы (1) устойчиво.
0 системы (1) устойчиво.
б)
Если

 где
где ≥
0 – некоторая непрерывная функция
(W(0)=0,
W(y)≠0
при y≠0),
равна нулю лишь в начале координат, то
нулевое решение асимптотически
устойчиво.
≥
0 – некоторая непрерывная функция
(W(0)=0,
W(y)≠0
при y≠0),
равна нулю лишь в начале координат, то
нулевое решение асимптотически
устойчиво.
Теорема
имеет простой геометрический смысл.
Пусть n=2
и пусть линии V=c
(c=const)
замкнутые линии, содержащие начало
координат. Причем линия с меньшим
значением с лежит внутри линии с большим
значением с. Тогда (3) означает, что
интегральные линии, имеющие общую точку
с линией V=c,
не выходят из области, ограниченной
этой линией. Откуда и следует устойчивость
нулевых решений y1 0, y2
0, y2 0 (т.е. начало координат на плоскости
y1,
y2).
0 (т.е. начало координат на плоскости
y1,
y2).
При
выполнении более сильного условия (4),
интегральные линии пересекают линию
V c
снаружи внутрь (см. рис.), т.к.
c
снаружи внутрь (см. рис.), т.к.

 (
( > 0).
> 0).
 ,
следовательно, все интегральные линии,
при
,
следовательно, все интегральные линии,
при
 ,
→ к началу координат, что означает
асимптотическую устойчивость нулевого
решения.
,
→ к началу координат, что означает
асимптотическую устойчивость нулевого
решения.
Замечание:
заметим, что
левые части
неравенств (3) и (4) есть производные
 ,
взятые вдоль интегральных линий системы
(1). (Говорят, производная взята вдоль
системы (1).)
,
взятые вдоль интегральных линий системы
(1). (Говорят, производная взята вдоль
системы (1).)
Теорема Четаева о неустойчивости:
Если существует дифференцируемая функция V(y), удовлетворяющая в некотором замкнутом шаре Tr условиям:
в сколь угодно малой окрестности U начала координат
 областьU0,
в которой V>0,
причем V=0
на лежащей в U
части границы U0;
областьU0,
в которой V>0,
причем V=0
на лежащей в U
части границы U0;в области U0 производная
 ,
причем в области, где
,
причем в области, где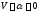 ,
производная
,
производная ,
,
то
нулевое решение системы (1) неустойчиво.
y1 0, y1
0, y1 0,…,yn
0,…,yn 0.
0.
Зад. Исследовать на устойчивость нулевое решение системы:
Пример
1:

 (
( –
эта пара функций образует нулевое
решение системы)
–
эта пара функций образует нулевое
решение системы)
 (функция
V-неотрицательная,
имеет непрерывные частные производные,
обращается в 0 в единственной точке)
(функция
V-неотрицательная,
имеет непрерывные частные производные,
обращается в 0 в единственной точке)

Условие
(3) выполнено,
 нулевое решение устойчиво. Асимптотической
устойчивости нет. Интегральными линиями
будут окрестности, которые при
нулевое решение устойчиво. Асимптотической
устойчивости нет. Интегральными линиями
будут окрестности, которые при не → к нулю.
не → к нулю.
Пример
2:






Нулевое
решение асимптотически устойчиво.
Пример 3:



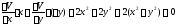 при
при
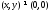
 по
теореме Четаева нулевое решение
неустойчиво.
по
теореме Четаева нулевое решение
неустойчиво.
Метод функций Ляпунова оказывается универсальным и эффективным методом для широкого круга задач теории устойчивости. Недостаток метода в том, что не существует достаточно общего конструктивного способа для нахождения функций Ляпунова.
В простейших случаях функции Ляпунова следует искать в виде:







Пусть функции (1) fi имеют вид:

 где
где



Теорема Ляпунова об устойчивости по первому приближению:
Пусть

При
всех x
≥ x0
и при всех y,
с достаточно малой нормой ||y||,
норма
 (α, М -const),
и функции gi
непрерывны по совокупности переменных.
Тогда, если действительные части всех
корней уравнения | λE
– A
| = 0 отрицательны, то нулевое решение
системы (1) асимптотически устойчиво.
Если хотя бы один из корней имеет
положительную действительную часть,
то нулевое решение не устойчиво. Без
док-ва.
(α, М -const),
и функции gi
непрерывны по совокупности переменных.
Тогда, если действительные части всех
корней уравнения | λE
– A
| = 0 отрицательны, то нулевое решение
системы (1) асимптотически устойчиво.
Если хотя бы один из корней имеет
положительную действительную часть,
то нулевое решение не устойчиво. Без
док-ва.
Для
определения знака действительной части
корня уравнения | λE
– A
| = 0 нет необходимости решать это
уравнение. Определитель нужно раскрыть
и записать его в виде многочлена
относительно λ:

 Для того, чтобы действительные
части всех корней уравнения (5) были
положительными, н. и д. выполнение одного
из условий:
Для того, чтобы действительные
части всех корней уравнения (5) были
положительными, н. и д. выполнение одного
из условий:
а) условие Гаусса – Гурвица: положительны все главные миноры матрицы Гурвица:







б) условие Льенара – Шипора: ai > 0 (i=1…n), миноры ∆n-1 > 0, ∆n-3 >0, ∆n-5 >0,… .
∆1
=
 ,
∆2
=
,
∆2
=
 ∆3
=
∆3
=
 ,…
.
,…
.
