14. Неявная и обратная функции. Экстремумы

Будем говорить, что ф-я y=f(x) задана неявно F(x,y)=0 в прямоугольнике К, К-это мн-во пар точек x, y: К={(x,y),a x b, c y d}, если x[a,b] выполн.рав-во F(x,f(x))=0,т.е. неявная ф-я явл. Решением ур-я, если F(x,f(x))=0.

Существование и дифференцируемость неявных функций.

Th(дост.условие существования непр. и дифф-ой неявн.ф-ции, определяемой ур-ем F(x,y)=0 (1)). Пусть 1) F(x,y) в окрестности т.(x₀, y₀) имеет непр.частн.производные F_x’ и F_y’ ; 2) F(x₀, y₀)=0 ; 3) F_y’(x₀, y₀)0. Тогда найдется прямоугольник К, состоящий из пар чисел: К={(x,y),x₀ - a x  x₀+a, y₀ - b y y₀+b}, в кот.ур-е (1) определяет y как неявн.ф-цию от x. Ф-ция y=f(x)-непр.-дифф-ма в инт.(x₀-a,x₀+a) и ее производная выч-ся по ф-ле:

Ф-я не обращается в ноль, непр-на,то она принимает либо положит.,либо отрицат.знач-я.

Пусть F_y’>0,найдется прямоугольник К₂.

Введем дополнит.ф-цию.

(y)=F(x₀,y) y₀ - b₂ y y₀ +b₂

’(y)=F_y’(x₀,y)>0

(y) (y₀)=F(x₀,y₀)=0

(y₀ – b₂)<0, (y₀ + b₂)>0 ф-ция -непр.

В окрестностях точек (y₀-b₂) и (y₀-b₂) ф-ция  сохраняет свой знак.

x₀ – a₂  x <x₀ , x₀< x <x₀+a₂ a₂ < a₁

y₀ – b₂  y  y₀ + b₂ b₂ < b₁

Для x из отрезка: x [x₀ – a₂ , x₀ + a₂]

F(x , y₀ - b₂)<0 , F(x , y_{0 +} b₂)>0

Выбираем некот.т-ку x^* [x₀ – a₂ , x₀ + a₂]

^*(y)=F(x^*,y) ^*(y₀ – b₂)<0 ^*(y₀ + b₂)>0

^* непр.,на концах отрезка принимает знач-я разн.знаков   точка y^*[y₀ – b₂, y₀ + b₂], что ^*(y^*)=0=F(x^*,y^*) x^*-единств.,т.к. ^*-возр-щая, каждому y^* нашли единств. x^*,  ур-ие F(x,y)=0 зпдает y, как неявн.ф-цию y=f(x).

Док-ли,что задан.ф-ция неявна. Док-ем,что дифф-ма.

Док-ем,что неявн.ф-ция дифф-ма в прямоуг. К₂.

(x,y) – задана, выбираем т. (x₀ +x,y₀ +y)K₂. y=f(x)

y+y=f(x+x) F(x,y)=0

F(x,y)+ F(x+x,y+y)=0 - F(x,y)+ F(x+x,y+y)=0

F(x+x,y+y) - F(x,y) =(по Th Лагранжа)=Fx’(x+x,y+y0)x+ F_y’(x+x,y+y)y= 0

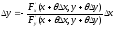x0 y0 F_y’ >0  0 <   F_y’   - ф-ция принимает свои наиб. и наим. знач-я.

₁  |F_x’ |  ₁ |y | 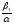 |x | 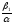- const  y0

Вычисление производных неявных функций.

Опр. Пусть задано ур-е F(x₁,x₂,…,x_n ,y)=0 (2).Будем говорить,что в n+1-мерном параллелепипеде ур-е (2) определяет y как однозначную ф-цию от x₁,…,x_n ,если каждому набору x₁,…,x_n соотв-ет один и только один y, причем:

П=[x₁⁰-a₁ , x₁⁰+a₁] [x₂⁰-a₂ , x₂⁰+a₂]… [x_n⁰-a_n , x_n⁰+a_n][y₀ –b,y₀+b]

(x₁,x₂,…,x_n) [x₁⁰-a₁ , x₁⁰+a₁] [x₂⁰-a₂ , x₂⁰+a₂] … [x_n⁰-a_n , x_n⁰+a_n] y[y₀ –b,y₀+b]

Th Пусть выполнены усл-я: 1) F(x₁,…,x_n ,y) непр-на и имеет в некот.окрестности т.(x₁⁰,…,x_n⁰,y⁰) и имеет непр.частную произв-ю; 2) F(x₁⁰,…,x_n⁰,y⁰)=0 ; 3) F_y’(x₁⁰,…,x_n⁰,y⁰)0 ,тогда найдется такой параллелепипед В, в кот. Ур-е (2) опред-ет y как неявн.ф-ю от (x₁,…,x_n):

Ф-ция y=f(x₁,…,x_n) имеет непр.частн.произв-е в параллепепиде [x₁⁰-a₁ , x₁⁰+a₁]… [x_n⁰-a_n , x_n⁰+a_n], причем справедлива ф-ла:

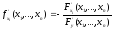
Системы функций и векторные функции.

Опр. Если каждому значению tE, где E – некот.множ-во чисел,соответсвует определенный вектор r=r(t) трехмерного прос-ва, то будем говорить, что на Е определена вектор-функция,или векторная функция r(t).

Теоремы об обратной функции.

Лемма 1.Пусть функция f строго возрастает (убывает) на некотором множестве XR и пусть Y — множество ее значений. Тогда обратная функция f^--1 является однозначной строго возрастающей (убывающей) функцией на множестве Y.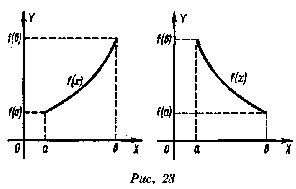

Теорема 3. Пусть функция f определена, строго возрастает (убывает) и непрерывна на отрезке [а, b], тогда обратная функция f^-x определена, однозначна, строго возрастает (убывает) и непрерывна на отрезке с концами в точках f(a) и f(b) (рис).

Теорема 4. Пусть функция f определена, строго возрастает (убы­вает) и непрерывна на интервале (а, b) (конечном или бесконечном) и пусть .Тогда обратная функция f ^-1 оп­ределена, однозначна, строго возрастает (убывает) и непрерывна на интервале (конечном или бесконечном) с концами c и d (рис. 25). При этом в случае, когда а=-∞ под понимается предел , а в случае b=+∞ под пределом 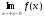- предел .

Теоремы о зависимости и независимости системы функций.

Экстремум функции нескольких переменных.

Опр. Пусть дана ф-я y=f(x₁,…,x_n) ; D(f)=M  Rⁿ ; x⁰=(x₁⁰,…,x_n⁰) –внутр.т.для обл. M

Ф-я y=f(x), где x=(x₁,…,x_n) имеет в т. x⁰ М максимум(минимум), если ее можно окружить такой окрестностью (x⁰-, x⁰+) ( (x⁰-, x⁰+) –n-мерный параллелепипед),что  x (x⁰-, x⁰+) выполн-ся нер-во: f(x) f(x⁰) ( f(x) f(x⁰) ) (*)

(x⁰-, x⁰+)=(x₁⁰-, x₁⁰+)(x₂⁰-, x₂⁰+)…(x_n⁰-, x_n⁰+) f(x₁,…,x_n) f(x₁⁰,…,x_n⁰)

Замеч. Нер-ва (*) можно записать в виде f=f(x)-f(x⁰)<0 (f=f(x)-f(x⁰)0)

Необходимые условия экстремума, достаточные условия экстремума.

Th (Необх.усл.экстремума) Если x₀ –т.локального экстремума ф-ии,то в этой т. ф-я либо не дифф-ма, либо она дифф-ма и ее градиент равен 0.

Замеч. Т.К. все частные произв-е в случае дифф-ти ф-ии обращ-ся в 0, то дифф-ал ф-ии в этой т.также равен 0  если т.x₀ – т.локального экстр-ма,то дифф-ал ф-ции в этой т. либо не , либо = 0.

Опр.Точка,в кот. дифф-ал =0 или не  наз. критической точкой. Критич.т.,в кот. отсутствует экстремум наз. седловой точкой.

Достаточное условие экстремума.

Дано: f-ф-я n-переменных; M RⁿR ; x₀M⁰-мн-во внутр.точек. В окр.т. x₀ ф-я f имеет непр.частн.произв-ые 2-го порядка ( смешанные частн.произв.совпадают).

Замеч. Если d²f(x₀,x)0 при некот. x,то в некот.окр-ти т. x₀ знак 2-го дифф-ла сохр-ся.

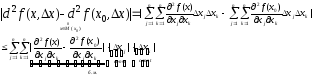
Учитывая окр-ть,где вторые произв-ые непр., получим,что |разность| (в нер-ве) может быть сколь угодно малой, разность дифф-лов сколь угодно малая, знаки d²f(x,x) и d²f(x₀,x) совпадают.

Th Пусть x₀ –критич. т. ф-ции f 1) если d²f(x₀,x) –положит. определен. квадратичн. форма,то x₀ –т. локальн. минимума; 2) если d²f(x₀,x) –отрицат. определен. квадратичн. форма,то x₀ –т. локальн. максимума; 3) если d²f(x₀,x) –знакоперемен. квадратичн. форма,то x₀ – седловая точка.

Понятие об условном экстремуме.

f : M RⁿR ; x₀M⁰ ; y=f(x₀,…,x_n)

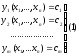m<n

Опр. Ф-я f при наличии связи (1) имеет в т. x⁰ ,корд-ты кот. удовл-т сис-ме (1), условный max(min), если найдется окр-ть т. x⁰ такая, что  x U(x⁰) : f(x) f(x⁰) ( f(x) f(x⁰) )

Пусть в окр-ти т. x⁰ ф-ции u₁,…,u_m непрерывны, причем выполнено усл-е:

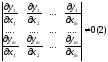якобиан

Th Если т. x⁰ – т. лок. усл. экстр-ма ф-ии f при условии (1), то найдутся такие постоянные ₁,…,_m, что в этой т. вып-ся рав-во:

Общая схема отыскания наибольших и наименьших значений функции нескольких переменных.

Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи g(x,y)=C удалось разрешить относительно одной из переменных, например, выразить y через x: y=φ(x). Подставив полученное выражение в функцию двух переменных, получим z=f(x,y)=f(x, φ(x)) то есть функцию одной переменной. Ее экстремум и будет условным экстремумом функции z=f(x,y).

Исследование функции двух переменных на экстремум

1.      Найти частные производные функци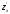и и.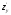

2.      Решить систему уравнений = 0 и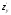= 0 и найти критические точки функции.

3.      Найти частные производные второго порядка, вычислить их значения в каждой критической точке и с помощью достаточного условия сделать вывод о наличии экстремумов.

4.      Найти экстремумы (экстремальные значения) функции.

Для отыскания условного экстремума в общем случае используется метод неопределенных множителей Лагранжа.

Рассмотрим функцию трех переменных .

Эта функция называется функцией Лагранжа, а  - множителем Лагранжа.

Если точка является точкойусловного экстремума функции при условии, то существует значение ₀ такое, что точка являетсяточкой экстремума функции .

 Таким образом, для нахождения условного экстремума функции при условиитребуется найти решение системы

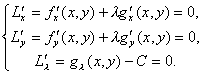
Последнее из этих уравнений совпадает с уравнением связи.