
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
29. Разностные методы решения задач математической физики.
Уравнения математической физики
Рассматриваются классические уравнения математической физики. Это уравнения с двумя независимыми переменными: t - временем и пространственными координатами (декартовыми, цилиндрическими или сферическими).
Задача называется стационарной, если ее решение не зависит от времени, и нестационарной или эволюционной, если оно зависит от времени. Задачи с одной пространственной переменной называются одномерными, с двумя - двумерными, с тремя - трехмерными.
Каноническая
форма уравнений с двумя независимыми
переменными имеет вид:
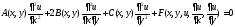 ,
гдеA,B,C
имеют непрерывные производные второго
порядка и не обращаются одновременно
в 0.
,
гдеA,B,C
имеют непрерывные производные второго
порядка и не обращаются одновременно
в 0.
Пусть
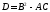 .
ЕслиD=0,
ур-е параболическое, D>0
– гиперболическое, D<0
– эллиптическое.
.
ЕслиD=0,
ур-е параболическое, D>0
– гиперболическое, D<0
– эллиптическое.
Рассмотрим
некоторую задачу, определяемую
дифференциальным уравнением и граничными
условиями. Запишем ее в операторной
форме:
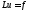 (1),
гдеL
- некоторый
дифференциальный оператор, действующий
на искомую функцию и, f
- правая часть. Будем считать, что
оператор L
включает
как дифференциальные уравнения, так и
граничные условия. На некоторой
разностной сетке строим разностный
оператор
(1),
гдеL
- некоторый
дифференциальный оператор, действующий
на искомую функцию и, f
- правая часть. Будем считать, что
оператор L
включает
как дифференциальные уравнения, так и
граничные условия. На некоторой
разностной сетке строим разностный
оператор
 ,
действующий на сеточную функцию
,
действующий на сеточную функцию .
Примером дифференциального оператора
является оператор Лапласа
.
Примером дифференциального оператора
является оператор Лапласа
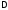 ,
а соответствующий ему разностный
оператор возникает при аппроксимации
вторых производных разностными
отношениями. При подстановке точного
решения уравнения (1) в оператор
,
а соответствующий ему разностный
оператор возникает при аппроксимации
вторых производных разностными
отношениями. При подстановке точного
решения уравнения (1) в оператор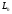 , имеем:
, имеем:
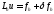 ,
где величина
,
где величина
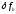 называется
невязкой.
называется
невязкой.
Разностная
схема называется аппроксимирующей
на решении,
если норма невязки стремится к нулю
при стремлении к нулю шага разностной
схемы, т.е.
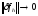 при
при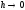 .
Если при этом норма невязки удовлетворяет
условию
.
Если при этом норма невязки удовлетворяет
условию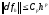 и
константаСр
не зависит
от
и
константаСр
не зависит
от
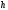 ,
то говорят, что разностная схема имеетр -й
порядок аппроксимации или разностная
схема аппроксимирует дифференциальный
оператор с порядком р.
,
то говорят, что разностная схема имеетр -й
порядок аппроксимации или разностная
схема аппроксимирует дифференциальный
оператор с порядком р.
Разностная
схема называется сходящейся,
если норма разности точного и
приближенного решений
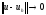 стремится
к нулю при стремлении к нулю шага
разностной сетки.
стремится
к нулю при стремлении к нулю шага
разностной сетки.
Если
при этом
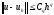 , то говорят, что разностная схема имеетq
-й порядок
точности или имеет место сходимость с
порядком q.
, то говорят, что разностная схема имеетq
-й порядок
точности или имеет место сходимость с
порядком q.
Порядок аппроксимации ду не всегда совпадает с порядком точности разностной схемы, так как порядок точности разностной схемы зависит как от аппроксимации ду, так и от аппроксимации граничных условий. Не всякая аппроксимирующая схема является сходящейся.
В связи с этим важным является понятие устойчивости разностной схемы.
Устойчивостью
разностной схемы называется непрерывная
зависимость решения разностной
задачи от правых частей и граничных
условий. Для линейного оператора схема
устойчива, если
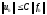 где С - константа, не зависящая от шага
разностной сетки и входных условий
где С - константа, не зависящая от шага
разностной сетки и входных условий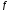 .
.
Метод
сеток. 
Метод сеток (или метод конечных разностей) сводит решение систем уравнений в частных производных к решению систем, как правило, линейных алгебраических уравнений с достаточно разреженными матрицами. При этом решение уравнения методом сеток можно разделить на три этапа:
1)
Область непрерывного изменения
аргумента (или аргументов) заменяется
конечным дискретным множеством
точек, называемых разностной сеткой.
Для этого проводятся прямые, параллельные
осям координат. Расстояние между двумя
параллельными прямыми наз-ся шагом
сетки. Шаги по осям могут быть различными.
Точки пересечения прямых
 наз-ся узлами разностной сетки. В
разностной сетке выделяются внутренние
и граничные узлы. Решение разыскивается
во внутренних узлах, а в граничных
узлах задается значение искомой
функции или находится с помощью
аппроксимации из граничных условий
исходной задачи. Множество всех узлов,
расположенных в области и на границе
явл-ся сеточной областью. Функция
дискретного аргумента, определенная
на разностной сетке, называется
сеточной функцией.
наз-ся узлами разностной сетки. В
разностной сетке выделяются внутренние
и граничные узлы. Решение разыскивается
во внутренних узлах, а в граничных
узлах задается значение искомой
функции или находится с помощью
аппроксимации из граничных условий
исходной задачи. Множество всех узлов,
расположенных в области и на границе
явл-ся сеточной областью. Функция
дискретного аргумента, определенная
на разностной сетке, называется
сеточной функцией.
2) Ду и граничные условия заменяются по определенным правилам своими разностными аналогами. Разностные операторы, соответствующие ду, записываются во внутренних узлах.Разностные операторы, соответствующие граничным условиям, записываются в граничных узлах. В результате получается система алгебраических уравнений, число которых пропорционально числу внутренних узлов сеточной области. При замене дифференциального оператора разностным аналогом выбирают шаблон разностной схемы - набор (конфигурацию) узлов, с использованием которых производится замена производных конечными разностями. Шаблон, содержащий р точек, называется р – точечным.
3) Осуществляется решение системы алгебраических уравнений каким-либо из известных методов. В большинстве случаев полученная система уравнений есть система линейных алгебраических уравнений очень большого порядка, но с очень разреженной матрицей. В случае нелинейных систем итерационные процедуры, как правило, сводят их к линейным системам.
Классическим
примером уравнения параболического
типа явл-ся уравнение теплопроводности
или диффузии
в области
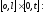
 ,
где
,
где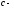 коэффициент
теплопроводности (если
коэффициент
теплопроводности (если -температура) и массопроводности (если
-температура) и массопроводности (если -
концентрация).
-
концентрация).
Неявная разностная схема для уравнения теплопроводности имеет вид:
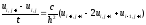 .
Здесь
.
Здесь
 соответствует пространственной, а
соответствует пространственной, а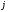 -
временной координате. В отличие от
явной схемы, для вычисления в правой
части уравнения используются значения
функции на том же самом временном шаге.
Пусть
-
временной координате. В отличие от
явной схемы, для вычисления в правой
части уравнения используются значения
функции на том же самом временном шаге.
Пусть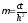 ,
тогда
,
тогда ,
или
,
или .
В матричной форме это уравнение имеет
вид:
.
В матричной форме это уравнение имеет
вид:
 ,
где
,
где

Классическим
примером уравнения гиперболического
типа явл-ся уравнение колебаний
струны:
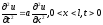 ,
где
,
где -
отклонение струны от положения
равновесия,
-
отклонение струны от положения
равновесия, -
скорость перемещения колебаний.
-
скорость перемещения колебаний.
Используя
разностные аналоги для частных
производных
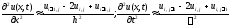 ,
запишем уравнение в конечных разностях
,
запишем уравнение в конечных разностях
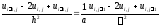 .
Здесь индекс
.
Здесь индекс
 соответствует пространственной, а
соответствует пространственной, а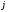 -
временной координате. Полученное
уравнение позволяет выразить значение
функции
-
временной координате. Полученное
уравнение позволяет выразить значение
функции в момент времени
в момент времени через значения функции в предыдущие
моменты времени
через значения функции в предыдущие
моменты времени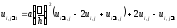 .
Это явная разностная схема, т.к. искомая
величина получается в явном виде. Она
устойчива, если
.
Это явная разностная схема, т.к. искомая
величина получается в явном виде. Она
устойчива, если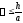 .
.
№ 30. Обыкновенные дифференциальные уравнения первого порядка.
ОДУ
наз. ур-е
 (1),y-неизв.
ф-я от x.
(1),y-неизв.
ф-я от x.
Порядком ДУ наз. наивысший порядок входящей в него производной.
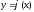 определенная
на некотором промежутке<a,b>
наз.решением
ДУ, если
после замены y
на
определенная
на некотором промежутке<a,b>
наз.решением
ДУ, если
после замены y
на
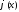 ,
,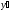 на
на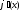 и т.д. оно обращается в тождество. ДУ
может иметь множество решений.
и т.д. оно обращается в тождество. ДУ
может иметь множество решений.
Основной задачей теории ДУ является отыскание всех решений данного ДУ. В простейшем случае задача сводится к вычислению интеграла.
Решение наз. интегралом, а процесс интегрированием.
График
решения ДУ
наз. интегральной кривой. Пр.
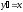 ,
,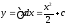 .
Для определения постоянной необходимо
задать доп. ус-я, которые обычно вытекают
из постановки задачи. В общем случае
ДУ может содержатьn-произ.постоянных.
Доп.усл-я: x=x0;
y(x0)=y0;..;
.
Для определения постоянной необходимо
задать доп. ус-я, которые обычно вытекают
из постановки задачи. В общем случае
ДУ может содержатьn-произ.постоянных.
Доп.усл-я: x=x0;
y(x0)=y0;..;
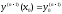 (2).
Задача отыскания ф-и, удовл. (1)(2) наззадачей Коши.
Пусто обл.G
содержится в (n+1)
мерном пр-ве. Для широкого класса
уравнений (1) и нач.ус из G
ур-е(1) имеет единственное решение,
следовательно интегральные кривые
зависят от нач.усл., причем при n=1
мн-во интегральных кривых без пересечения
покрывает обл.G.
Такие реш.наз частными
реш.зад.Коши(1-2). Мн-во всех ч.р.образует
общ.реш. Общее
решение
– ф-я
(2).
Задача отыскания ф-и, удовл. (1)(2) наззадачей Коши.
Пусто обл.G
содержится в (n+1)
мерном пр-ве. Для широкого класса
уравнений (1) и нач.ус из G
ур-е(1) имеет единственное решение,
следовательно интегральные кривые
зависят от нач.усл., причем при n=1
мн-во интегральных кривых без пересечения
покрывает обл.G.
Такие реш.наз частными
реш.зад.Коши(1-2). Мн-во всех ч.р.образует
общ.реш. Общее
решение
– ф-я
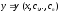 ,
что при соотв. выборе с1,.,сn
получается любое решение уравнения
(1) с нач.ус. в G.
,
что при соотв. выборе с1,.,сn
получается любое решение уравнения
(1) с нач.ус. в G.
Поле
направлений.
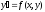 (3),f(x,y)
опред. в нек.обл.Д. Посмотрим геометрически.
(3),f(x,y)
опред. в нек.обл.Д. Посмотрим геометрически.
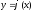 реш.,
реш.,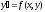 угловой
коэф касат к этой кривой. С геом т зр
ур(3) задает в каждой точке области Д
значение углового коэф касс, прох ч/з
эту т к гр реш ур(3)., т.е.(3) опр в каж т
(x,y)
принадл. Д касательную к искомой
интегральной кривой, т.о. ур(3) определяет
поле напрвления.
Щадача интегрального уравнения
заключается в том, чтобы найти кривые
касс к кот в каж т совпадают с пр определен
полем. Такое истолкование ДУ и
интегрирование дает графический способ
решения ур-я наз. метод
изоклин.
Сначала на пл-ти XOY
проводем линию, вдоль которой ф-я f(x,y)
имеет постоянное значение=P.
Эту линию интегральные кривые пересекают
под одним углом в направлении оси OX
tg
которого = P
=
угловой
коэф касат к этой кривой. С геом т зр
ур(3) задает в каждой точке области Д
значение углового коэф касс, прох ч/з
эту т к гр реш ур(3)., т.е.(3) опр в каж т
(x,y)
принадл. Д касательную к искомой
интегральной кривой, т.о. ур(3) определяет
поле напрвления.
Щадача интегрального уравнения
заключается в том, чтобы найти кривые
касс к кот в каж т совпадают с пр определен
полем. Такое истолкование ДУ и
интегрирование дает графический способ
решения ур-я наз. метод
изоклин.
Сначала на пл-ти XOY
проводем линию, вдоль которой ф-я f(x,y)
имеет постоянное значение=P.
Эту линию интегральные кривые пересекают
под одним углом в направлении оси OX
tg
которого = P
=
 .
ПридаваяP
ряд значений получим ряд изоклин –
линии постоянного наклона интегральных
кривых. Затем на изоклинах расставим
стрелки под таким углом в полож.напр.
OX,
чтобы tg=P.
Для получения приближ граф решур-я с
нач усл x=xo,
y=y0
надо исходя из т с корд x0,y0
провести кр т.о., чтобы она пересекала
изоклины так, как указ стрелки на
изоклинах. Т.О с помощью изоклин строится
приближ гр некот реш ДУ.
.
ПридаваяP
ряд значений получим ряд изоклин –
линии постоянного наклона интегральных
кривых. Затем на изоклинах расставим
стрелки под таким углом в полож.напр.
OX,
чтобы tg=P.
Для получения приближ граф решур-я с
нач усл x=xo,
y=y0
надо исходя из т с корд x0,y0
провести кр т.о., чтобы она пересекала
изоклины так, как указ стрелки на
изоклинах. Т.О с помощью изоклин строится
приближ гр некот реш ДУ.
Метод ломанных Эйлера. yш = f(x,y) y(x0)=y0; yш=f(x,y); рассмотрим некоторую т(x0,y0) принад обл Д. Проведем ч/з нее касательную. Найдем f в этой точки. На этой касательной возьмем т.(x1,y1).проведем еще одну касательную. Получим график – ломанную Эйлера.
Ур-я
с разделяющимися переменными.:Д.у.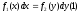 наз ур-м с раздел. перем.
наз ур-м с раздел. перем.
Общий
интеграл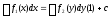
Линейные
уравнения:
ур=е вида
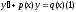 ,
гдеp(x)
и q(x)-известные
функции, наз. линейным д.у. 1-го порядка.
Ур-е линейно,т.к. оно линейно относительно
y
и
,
гдеp(x)
и q(x)-известные
функции, наз. линейным д.у. 1-го порядка.
Ур-е линейно,т.к. оно линейно относительно
y
и
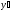 .
Предп-ся, чтоp(x)
и q(x)-непрерывные
функции. Р-е в виде
.
Предп-ся, чтоp(x)
и q(x)-непрерывные
функции. Р-е в виде
 (2),
гдеu,v-неизвестные
фунции от х, тогда
(2),
гдеu,v-неизвестные
фунции от х, тогда
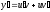 (3).
(2)и (3) в (1):
(3).
(2)и (3) в (1):
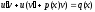 (4).
Выберем v
так,чтобы
(4).
Выберем v
так,чтобы
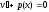 ,
,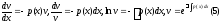 .
В силу выбора 2-е слагаемое=0,тогда(4):
.
В силу выбора 2-е слагаемое=0,тогда(4):
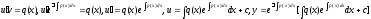
Ур-я в полных дифференциалах. Полный диф-л ЭP=ЭQ; ДУ вида P(x,y)dx + Q(x,y)dy=0 наз уравнением полных диф-лов, если левая часть есть полный диф-л некот ф-и. Пусть ЭP=ЭQ, тогда найдется ф-я du=P(x,y)dx = Q(x,y)dy=0; dU=0; u(x,y)=c. Для нахождения общ инт ур-я надо найти u(x,y) и приравнять к постоянной. Ф-я u(x,y)м/б найдена сл обр. du=(эu/эx)dx + (эu/эy)dy = P(x,y)dx + Q(x,y)dy; эu/эx=P(x,y); эu/эy=Q(x,y); U(x,y) = инт P(x,y)dx + (y); du/dy = (э(инт P(x,y)dx)/эy) + ш(y) = Q(x,y); ш (y) = Q(x,y)-(э(инт P(x,y)dx/эy). Получаем (y) и подставляем в ур-е и получаем u(x,y)=с.
№ 31 Теорема Пеано. Теорема Коши.
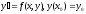 -
задача
Коши (1)
-
задача
Коши (1)
Теорема
Пеано: Если
функция f(x,y)
непрерывна и ограничена в обл.G,то
через каждую т.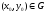 проходит по крайней мере одна интегральная
кривая уравнения
проходит по крайней мере одна интегральная
кривая уравнения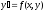 .
.
В
условии т.Пеано через т. могут проходить 2 интегральные кривые,
покажем это:
могут проходить 2 интегральные кривые,
покажем это:
Пример:
 непрерывна
на всей плоскости и ограничена на любой
ограниченной обл. G,
поэтому она удовлетв. Условию
т.Пеано,однако,
непрерывна
на всей плоскости и ограничена на любой
ограниченной обл. G,
поэтому она удовлетв. Условию
т.Пеано,однако,
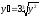 имеет
2интегр. кр., проход. через т.(0,0): 1) у=0;
2)
имеет
2интегр. кр., проход. через т.(0,0): 1) у=0;
2)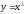 ,
поэтому т.Пеано явл. Теоремой существоания,
но не единственности реш-я задачи Коши.
,
поэтому т.Пеано явл. Теоремой существоания,
но не единственности реш-я задачи Коши.
Дана
задача Коши (1). Функция f(x,y)
удовлетв. в обл. G
условию Липшеца по у, если


 (2).
(2).
Если
f(x,y)
имеет ограничен.
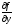 вG,
кот. Вместе с
вG,
кот. Вместе с
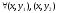 содержат соединяющий их отрезок, то
она удовл. усл. Липшеца.
содержат соединяющий их отрезок, то
она удовл. усл. Липшеца.
Теорема о существовании и единственности р-я задачи коши для ур-й 1-го порядка:
Если
f(x,y)
определена и непрерывна в некоторой
обл.G,
содержащей т.
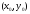 и удовлет. ВG
условию липшеца по у, то на некотором
и удовлет. ВG
условию липшеца по у, то на некотором
 существует единственное р-е
существует единственное р-е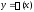 задачи коши (1).
задачи коши (1).
Док-во:
По
т.Пеано задача (1) имеет р-е на
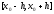 покажем, что это р-е единственно, еслиh>0
и Nh<1.
Т.к.
покажем, что это р-е единственно, еслиh>0
и Nh<1.
Т.к.
 р-е (1) на
р-е (1) на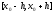 ,то
,то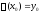 и
и интегрируя это тождество между
интегрируя это тождество между иx,
кот. содержится в
иx,
кот. содержится в
 .
.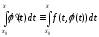 ,
,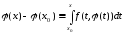 ,
,
 .
Пусть
.
Пусть
 -произвольное
р-е (1) на
-произвольное
р-е (1) на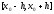 .
Ан-но (3) получим:
.
Ан-но (3) получим:
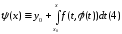 .
Из (3) и (4):
.
Из (3) и (4):


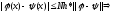
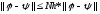 ,
,

Т.е.
р-е задачи Коши единственное на
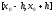 .
Ч.т.д.
.
Ч.т.д.
Продолжений
решений:
Опр: решение
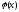 какого-либо д.у.,заданной на
какого-либо д.у.,заданной на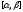 назовем продолжаемым вправо(влево),если
сущ. р-е
назовем продолжаемым вправо(влево),если
сущ. р-е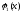 того же ур-я на
того же ур-я на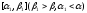 и
и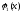

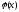 на
на .
Р-е не продолжаемое ни вправо, ни влево
наз непродолжаемым.
.
Р-е не продолжаемое ни вправо, ни влево
наз непродолжаемым.
Гладкость
р-я:
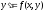 ,(*)
где
правая часть непрерывна.
,(*)
где
правая часть непрерывна.
Теорема: если f(x,y) имеет непрерывные производные по x и у до p-го порядка (p>=1), то всякое решение д.у.(*) имеет непрерывные производные по x до (p+1) порядка.
№ 32 Основные понятия
Уравнения вида
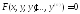 (1)
(1)
где y неизвестная функция от x, называется обыкновенным дифференциальным уравнением.
Порядком дифференицального уравнения называется наивысший порядок входящих в него производных.
Функция
 ,
определенная на некотором промежутке
< a, b >, называется решением
дифференциального уравнения (1), если
после замены y на
,
определенная на некотором промежутке
< a, b >, называется решением
дифференциального уравнения (1), если
после замены y на ,
, на
на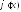 ,...,y(n)
на
,...,y(n)
на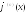 оно обращается в тождество.
оно обращается в тождество.
Основной задачей теории дифференциальных уранений является отыскание всех решений данного дифференциального уравнения и изучение свойств этих решений. В простейших случаях эта задача сводится к вычислению интеграла. Поэтому решение дифференциального уравнения называют также его интегралом, а процесс нахождения этого решения интегрированием дифференцального уравнеия.
График решения дифференциального уравнения называется интегральной кривой.
Для определения произвольных постоянных, входящих в условие, необходимо задать дополнительные условие, которые обычно вытекают из поставленной задачи. Так в задаче 3 из такие условия были заданы в виде s(0) = s0 и v(0) = v0 , где s0 начальное расстояние, а v0 начальная скорость.
В общем случае уравнение (1) может иметь n произвольных постоянных. Для их определения можно можно задать дополнительные условия в виде
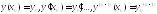 (2).Условия
(2) называются начальными условиями.
(2).Условия
(2) называются начальными условиями.
Задача отыскания функции, удовлетворяющей уравнению (1) и начальным условиям (2), называется задачей Коши.
Начальные условия (2) образуют координаты точки P (n +1)мерного пространства. Пусть область G содержится в (n +1)мерном пространстве. Для широкого класса уравнений (1) и начальных условий из G уравнение (1) имеет единственное решение. Такие решения называют частными решениями задачи Коши. Множества всех частных решений дифференциального уравнения образует общее решение в области G. Таким образом, интегральные кривые зависят от начальных условий, причем при n =1 множество интегральных кривых без пересечений покрывает область G.
Для уравнения (1) общее решение зависит от n произвольных постоянных:
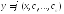 Для
получения частного решения из общего
решения указываются начальные условия,
по которым однозначно определяются
постоянные.
Для
получения частного решения из общего
решения указываются начальные условия,
по которым однозначно определяются
постоянные.
Существуют
и другие определения общего решения.
Часто называют общим решением функцию
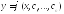 такую,
что при соответствующем выборе постоянных
такую,
что при соответствующем выборе постоянных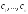 получается любое решение уравнения
(1) с начальными условиями в G.
получается любое решение уравнения
(1) с начальными условиями в G.
Общим решением зачастую называют совокупность всех частных решений, при этом область G не указывается.
Уравнения, допускающие понижение порядка
Рассмотрим
уравнение
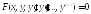 (3)
(3)
В ряде случаев это уравнение можно заменить эквивалентным уравнением более низкого порядка.
1.
y(n) =f (x)
Интегрируя n раз имеем:
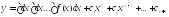
2. F (x, y(k), y(k+1), ..., y(n))=0
В уравнении отсутствует неизвестная функция и ее производная
до
(n-1)го порядка включительно. Порядок
уравнения может быть понижен до (n-k)
с помощью подстановки y(k) = z. В этом
случае уравнение примет вид:
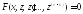
Если
найдено общее решение этого уравнения
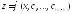 ,
то
,
то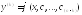
3.
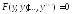
В
уравнении отсутствует x. Порядок
уравнения можно понизить с помощью
подстановки
 ,
здесь p рассматривается как новая
неизвестная функция, а y как независимая
переменная.
,
здесь p рассматривается как новая
неизвестная функция, а y как независимая
переменная.
 ,
,
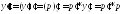
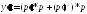
Аналогично
показывается, что все производные от
y по x выражаются через производные от
p по y порядка на единицу ниже подстановка
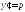 понижает
порядок уравнения на единицу.
понижает
порядок уравнения на единицу.
4.
Левая часть уравнеия (3) есть производная
функции
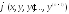
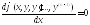 ,
,
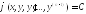 .
.
Т.е. порядок уравнения понижается на 1.
5.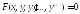 ,
где
,
где ,
т.е. функция F однородная относительно
y и ее производных. Порядок уравнения
можно понизить на 1 с помощью подстановки:
,
т.е. функция F однородная относительно
y и ее производных. Порядок уравнения
можно понизить на 1 с помощью подстановки:

Теорема существования и единственности для нормальной системы уравнений (задача Коши для системы уравнений)
Система
обыкновенных д.у. 1го порядка с n
неизвестными функциями назыв. нормальной,
если она имеет вид:
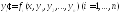 (4)
(4)
Система
функций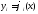 где i =1, ...n назыв. решением системы(4),
если при подстановке этих функций и их
производных в ур-е (4) эти ур-я
обращаются в тождество. Будем рассматривать
ур-е (4) при нач. усл-ях
где i =1, ...n назыв. решением системы(4),
если при подстановке этих функций и их
производных в ур-е (4) эти ур-я
обращаются в тождество. Будем рассматривать
ур-е (4) при нач. усл-ях
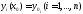 (5)
Задачу отыскания решений уря (4),
удовлетворяющих услям (5), будем
называть задачей Коши.
(5)
Задачу отыскания решений уря (4),
удовлетворяющих услям (5), будем
называть задачей Коши.
Т:
Пусть функции fi определены и непрерывны
в некоторой области
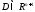 и содержащей точки с координатами
и содержащей точки с координатами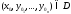 и пусть эти функции удовлетворяют
условию Липшица:
и пусть эти функции удовлетворяют
условию Липшица: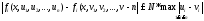 (6).Тогда
на некотором отрезке [x0 − h, x0 +h]существует
единственное решение задачи Коши (4)
(5).
(6).Тогда
на некотором отрезке [x0 − h, x0 +h]существует
единственное решение задачи Коши (4)
(5).
Теорема о существовании и единственности решений задачи Коши для уравнений n-го порядка
Пусть
дано уравнение
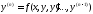 (7)
и заданы нач. условия
(7)
и заданы нач. условия
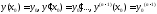 (8)
(8)
Т:
Пусть функция f определена и непрерывна
в некоторой области
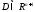
и
содержащей точки с координатами
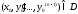 и
удовлетворяет условию Липшица:
и
удовлетворяет условию Липшица: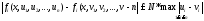 (9)
(9)
Тогда на некотором отрезке [x0 − h, x0 +h]существует единственное решение задачи Коши (7) (8).
Гладкость решений
Если
ф-и
 имеют
непрерывные производные по x и по y1,…,yn
до (p+1)го порядка (p ≥ 1), то всякое
решение нормальной системы д.у.
имеют
непрерывные производные по x и по y1,…,yn
до (p+1)го порядка (p ≥ 1), то всякое
решение нормальной системы д.у.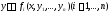 имеет
непрерывные производные по x до (p+1)го
порядка
имеет
непрерывные производные по x до (p+1)го
порядка
Док-во: р=1, тогда правая часть имеет непрерывную производную по х, значит левая часть также имеет непрерывную производную по х, сл-но, фун-я у(х) – имеет непрерывную производную 2-го порядка.(дальше нужно найти производную 2 порядка)
р=2, применяя те же рассуждения , получаем, что у(х_ имеет непрерывные производные 3-го порядка
