
- •5. Линейное пространство. Евклидово и унитарное пространства
- •6. Линейные операторы и их свойства
- •Линейные преобразования евклидова пространства
- •7. Действительные числа. Функция действительной переменной. Предел функции. Непрерывные функции.
- •8. Производная и дифференциал. Производные и дифференциалы высших порядков. Формула Тейлора
- •9. Основные теоремы дифференциального исчисления и их применения
- •10. Первообразная и неопределенный интеграл
- •4. Интегрирование некоторых тригонометрических функций.
- •6. Интеграл вида если функцияR является нечетной относительно cosx.
- •11. Определенный интеграл Римана, его свойства. Применения к вычислению геометрических, физических и механических величин Определенный интеграл
- •12. Функции нескольких действительных переменных.
- •13. Частные производные и дифференцируемость ф-ции в точке. Производные и дифференциалы высших порядков. Равенство смешанных производных
- •14. Неявная и обратная функции. Экстремумы
- •15. Числовые ряды и их сходимость.
- •16. Функциональные последовательности и ряды. Степенные ряды. Ряд Тейлора.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •18. Ряды Фурье. Преобразование Фурье. Интеграл Фурье
- •Разложение в ряд Фурье четных и нечетных функций
- •Разложение в ряд Фурье функций произвольного периода
- •Представление непериодической функции ряда Фурье
- •Тригонометрический ряд Фурье в комплексной области
- •Свойства ряда Фурье
- •- Неравенство Бесселя.
- •- Равенство Парсеваля,
- •Понятие об интеграле Фурье и об преобразовании Фурье
- •19. Мера Лебега, измеримые множества и функции
- •20. Интеграл Лебега и его свойства.
- •21. Ф-ции комплексной переменной. Диф-ние и инт-ние. Теорема Коши.
- •22. Ряды Тейлора и Лорана. Вычеты
- •Аналитические функции и их разложение в степенные ряды.
- •Свойства максимума модуля аналитических и гармонических функций.
- •Ряд Тейлора.
- •Ряд Лорана.
- •Изолированные особые точки аналитических функций и их классификация.
- •Вычеты и основная теорема о вычетах.
- •Применение к вычислению интегралов.
- •23. Математическое моделирование и вычислительный эксперимент
- •24. Численные методы в алгебре
- •Обусловленность систем линейных алгебраических уравнений
- •Вычисление определителей и обращение матриц
- •Итерационные методы
- •Достаточное условие сходимости итерационного процесса
- •25. Решение нелинейных уравнений и систем уравнений
- •26. Приближение функций.
- •27. Численное дифференцирование. Численное интегрирование
- •28. Решение обыкновенного дифференциального уравнения первого порядка методами Эйлера, Эйлера – Коши, Рунге – Кутты. Метод конечных разностей.
- •29. Разностные методы решения задач математической физики.
- •33. Линейные уравнения и системы.
- •34.Линейные уравнения и системы с постоянными коэффициентами
- •35. Устойчивость решений дифференциальных уравнений
- •Простейшие типы точек покоя. Автономные динамические системы двух уравнений первого порядка. Типы особых точек на фазовой плоскости
- •№37 Физические задачи, приводящие к уравнению параболического типа
- •Интеграл Пуассона
- •39. Алгебра логики
- •3. Основные законы логики.
- •4. Логические функции.
- •5. Нормальные формы. Совершенные нормальные формы.
- •Алгоритм построения сднф.
- •6. Арифметические операции в алгебре логики. Полином Жегалкина.
- •7. Полнота и замкнутость (примеры полных систем). Теорема Поста.
- •Свойства отношений.
- •40. Графы и их свойства
- •41. Маршруты в графах и деревья
- •41. Маршруты в графах и деревья
№37 Физические задачи, приводящие к уравнению параболического типа
l - длина стержня (стержень достаточно тонкий)
U1, U2 – температура на концах стержня
Линейное
распределение температуры:
 Количество
тепла, протекающего по поперечному
сечению стержняS
за единицу времени:
Количество
тепла, протекающего по поперечному
сечению стержняS
за единицу времени:

где k – коэффициент теплопроводности, зависящий от материала стержня.
Рассмотрим
процесс распространения температуры
в стержне. U(x,t)
– температура в сечении x
в момент времени t.
Количество тепла, протекающее через
сечение за промежуток
 :
: ,
гдеq
– плотность теплового потока.
,
гдеq
– плотность теплового потока.
 -закон
Фурье.
-закон
Фурье.
Интегральная
форма закона Фурье:

Количество
тепла, которое надо сообщить однородному
телу, чтобы повысить его температуру
на
 :
:
 ,
где с
– удельная теплоемкость. Если стержень
неоднороден, то
,
где с
– удельная теплоемкость. Если стержень
неоднороден, то

 -
плотность тепловых источников. В итоге
действия тепловых источников выделится
тепло:
-
плотность тепловых источников. В итоге
действия тепловых источников выделится
тепло:
 =>
=> .
Используя закон сохранения энергии,
теорему о среднем, теорему о конечных
приращениях получим уравнение
теплопроводности:
.
Используя закон сохранения энергии,
теорему о среднем, теорему о конечных
приращениях получим уравнение
теплопроводности:
Если
стержень однороден, то
 ,
где
,
где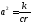 -коэффициент
теплопроводности,
-коэффициент
теплопроводности, .
.
Если
источники тепла отсутствуют, то

Уравнение
теплопроводности в
 :
:
Принцип максимального значения. Теорема единственности.
Теорема
1. Если функция
 определена и непрерывна в прямоугольнике
определена и непрерывна в прямоугольнике ,
удовлетворяющая уравнению теплопроводности
,
удовлетворяющая уравнению теплопроводности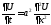 в точках открытого прямоугольника
в точках открытого прямоугольника ,
то минимальное и максимальное значения
функции
,
то минимальное и максимальное значения
функции достигаются или в начальные моменты,
или в точках границы
достигаются или в начальные моменты,
или в точках границы ,
, .
.
Теорема
2. Если две
функции
 ,
, определены и непрерывны в
определены и непрерывны в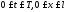 ,
удовлетворяют уравнению теплопроводности
,
удовлетворяют уравнению теплопроводности для
для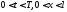 ,
одинаковы на начальных граничных
условиях
,
одинаковы на начальных граничных
условиях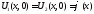 ,
, ,
, ,
то
,
то .
.
Следствие
1. Если два
решения
 ,
, уравнения теплопроводности удовлетворяют
условиям
уравнения теплопроводности удовлетворяют
условиям и
и ,
то
,
то .
.
Следствие
2. если три решения уравнения
теплопроводности
 удовлетворяют условию
удовлетворяют условию при
при ,
, ,
, ,
то эти же неравенства выполняются для
,
то эти же неравенства выполняются для при
при .
.
Следствие
3. Если для
двух решений теплопроводности
 ,
, имеет место неравенство
имеет место неравенство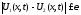 для
для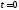 ,
, ,
, ,
то для
,
то для имеет место неравенство
имеет место неравенство при
при .
.
Теорема
3. Теорема
единственности на бесконечном промежутке.
Если
 ,
, непрерывны и ограничены во всей области
изменения переменныхx,t,
удовлетворяю уравнению теплопроводности
при
непрерывны и ограничены во всей области
изменения переменныхx,t,
удовлетворяю уравнению теплопроводности
при
 ,
, и условию
и условию для
для .
.
Метод разделения переменных. Однородная краевая задача.
Задача:
найти в непрерывной замкнутой области
 решение однородного уравнения
решение однородного уравнения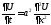 , где
, где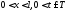 ,
удовлетворяющее начальному условию
,
удовлетворяющее начальному условию и однородным граничным условиям
и однородным граничным условиям .
.
Метод разделения переменных:
Найдем решение следующей задачи: решить уравнение
 ,
удовлетворяющее однородным граничным
условиям
,
удовлетворяющее однородным граничным
условиям .
Уравнение представимо в виде
.
Уравнение представимо в виде =>
=> =>
=> и
и ,
кроме того
,
кроме того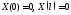 .
Мы получили задачу на собственные
значения – задача Штурма-Лаувиля:
.
Мы получили задачу на собственные
значения – задача Штурма-Лаувиля: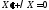
 для значения
для значения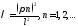 .
Существуют неправильные решения этой
задачи:
.
Существуют неправильные решения этой
задачи: .
Этим значениям соответствует решения
уравнения
.
Этим значениям соответствует решения
уравнения :
: .
В итоге получаем решение задачи:
.
В итоге получаем решение задачи: .
.Перейдем к решению основной задачи. Для этого составим формальный ряд:
 .
Функция
.
Функция удовлетворяет граничным условиям,
т.к. им удовлетворяют все члены ряда.
Из начальных условий =>
удовлетворяет граничным условиям,
т.к. им удовлетворяют все члены ряда.
Из начальных условий => =>
=> является коэффициентом Фурье функции
является коэффициентом Фурье функции при разложении ее в ряд поsin
в (0,l):
при разложении ее в ряд поsin
в (0,l):
 .
.
В силу принципа суперпозиции ряд составленный из частных решений тоже является решением.
Общая первая краевая задача
Найти
решение уравнения:
 с дополнительными условиями
с дополнительными условиями .
.
Будем
искать решение задачи в виде:
 .
Подставляя в исходное уравнение,
получим:
.
Подставляя в исходное уравнение,
получим: ,
где
,
где с дополнительными условиями:
с дополнительными условиями: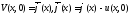 ,
, ,
, .
Функция
.
Функция выбирается таким образом чтобы
выбирается таким образом чтобы .
.
|=> Первая краевая задача решена.
