2.1 Точкові оцінки параметрів розподілу

У багатьох випадках треба дослідити кількісну ознаку Х генеральної сукупності, використовуючи результати вибірки. Часто для цього достатньо знайти наближені значення математичного сподівання , дисперсію , середньоквадратичне відхилення , початкові або центральні моменти випадкової величини Х.

Іноді з деяких міркувань вдається встановити закон розподілу Х. Тоді треба вміти оцінювати параметри цього розподілу.

Точкова оцінка деякого параметру розподілу визначається за даними вибірки, характеризується одним числом і служить оцінкою параметра розподілу генеральної сукупності.

Приведемо основні точкові оцінки параметрів розподілу.

Середнім арифметичним спостережуваних значень випадкової величини х називається частка від ділення суми всіх цих значень на їхню кількість, тобто

Вибірковою середньою називають середню арифметичну варіант вибірки з врахуванням їх частостей і позначають

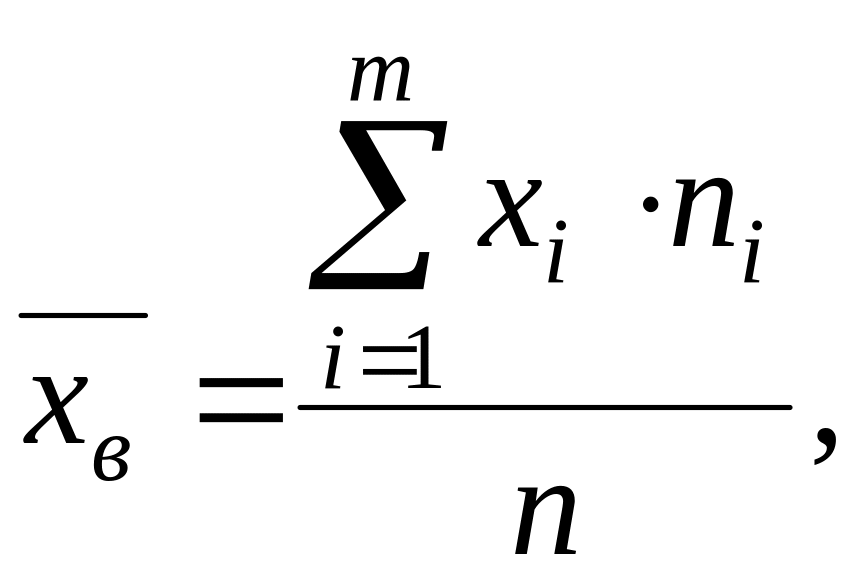
де: – значення і-ой варіанти; – частота варіанти; – об’єм вибірки; т – число різних варіант.

Основні властивості вибіркової середньої

1) При множенні усіх варіант вибірки на однаковий множник вибіркова середня також множиться на цей множник:

.

2) Якщо додати (відняти) до всіх варіант вибірки однакове число, то вибіркова середня зростає (зменшується) на це число

.

Ці властивості можна поєднати в одну формулу, яку називають формулою моментів

і використовують у статистиці.

Вибірковою дисперсією називають середню квадратів відхилення варіант від вибіркової середньої з врахуванням відповідних частостей

.

Якщо дані спостережень представлені у вигляді дискретного варіаційного ряду, причому – спостережувані варіанти, а – відповідні їм частоти, то вибіркова дисперсія спрощується, якщо її знаходити за формулою

,

Вибірковим середньоквадратичним відхиленням (стандартом) називають квадратний корінь із вибіркової дисперсії

.

Властивості

1) Дисперсія сталої величини дорівнює 0.

2) Якщо всі результати спостережень збільшити (зменшити) на деяке число с , то дисперсія й середнє квадратичне відхилення не зміниться, тобто

и. .

3) Якщо всі результати спостережень помножити на деяке число с , то має місце рівність:

або .

4) Якщо всі частоти варіант помножити на деяке число, то вибіркові дисперсія й середнє квадратичне відхилення не зміняться.

5) Вибіркова дисперсія дорівнює різниці між середнім арифметичним квадратів спостережень над випадковою величиною х і квадратом її середнього арифметичного, тобто

.

Виправлена вибіркова дисперсія:

.

Виправлене вибіркове середнє квадратичне відхилення:

.

Вибіркова асиметрія:

.

Вибірковий ексцес:

.

Якщо вибірка задана дискретним статистичним рядом

			...
			...

то у цьому випадку розрахункові формули мають вид

,

, де ,

,

, .

Приклад 1. Вибіркова сукупність задана таблицею

	1	2	3	4
	20	15	10	5

Знайти вибіркові характеристики.

Розв’язання. У даному випадку об’єм вибірки дорівнює . Знаходимо вибіркову середню

.

Знаходимо вибіркову дисперсію

.

Знаходимо вибіркове середньоквадратичне відхилення

Приклад 2. В результаті п’яти вимірів довжини виробу одним приладом (без систематичних похибок) отримані наступні результати в мм: 92; 94; 103; 105; 106.

Знайти:

а) вибіркове середнє довжини виробу;

б) вибіркову та виправлену дисперсії похибок приладу.

Розв’язання.

а) Знайдемо вибіркову середню

.

б) Знайдемо вибіркову дисперсію

.

в) Знайдемо виправлену вибіркову дисперсію

.

Медіана й мода

Медіаною називають значення варіанти, що доводиться на середину ранжованого ряда спостережень.

Якщо проведено непарне число спостережень , тоді

.

Якщо проведено парне число спостережень , тоді

.

Для інтервального варіаційного ряду медіану визначають за формулою

,

де: – нижня границя медіанного інтервалу;

– величина інтервалу;

– половина суми накопичених частот інтервального ряду розподілу;

– сума накопичених частот інтервалу, що передує медіанному;

– частота медіанного інтервалу.

Модою називають значення варіанти, що має найбільшу частоту в статистичному ряді розподілу.

У дискретних варіаційних рядах мода визначається без додаткових розрахунків за значенням варіанти, що має найбільшу частоту.

Для інтервального варіаційного ряду мода визначається за формулою

,

де: – нижня (мінімальна) границя модального інтервалу;

– величина інтервалу;

– частота інтервалу, що передує модальному;

– частота модального інтервалу;

– частота наступного за модальним інтервалу.

Приклад 3. Для варіаційного ряду знайти медіану й моду.

	0	1	2	3	4	5	7
	8	17	16	10	6	2	1

.

Приклад 4. Для інтервального варіаційного ряду знайти медіану й моду.

	14 – 18	18 – 22	22 – 26	26 – 30	30 – 34	34 – 38	38 – 42
	9	15	16	24	18	12	6

Розв’язання.

1) Для розрахунку медіани попередньо обчислюється стовпець накопичених частот.

	інтервали	частоти	накопичені частоти
1	14,0 – 18,0	9	9
2	18,0 – 22,0	15	24
3	22,0 – 26,0	16	40
4	26,0 – 30,0	24	64
5	30,0 – 34,0	18	82
6	34,0 – 38,0	12	94
7	38,0 – 42,0	6	100

2) Медіанним є (26,0 – 30,0), тому що на цей інтервал доводиться перша накопичена частота, що перевищує половину всього об'єму сукупності ( ).

3) Обчислимо :

,

де: – нижня границя медіанного інтервалу;

– величина інтервалу;

– половина суми накопичених частот;

– сума накопичених частот інтервалу, що передує медіанному;

– частота медіанного інтервалу.

4) Обчислимо ( модальний інтервал (26,0 – 30,0), тому що цей інтервал має найбільшу інтервальну частоту):

,

де: – нижня границя модального інтервалу;

– величина модального інтервалу;

– відповідно частоти перед модального, модального й після модального інтервалів.