ГЛАВА 11

ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.1. Основныепонятия

Ранее в курсе ТОЭ рассматривали цепи с сосредоточенными параметрами. В них можно выделить элементы, в которых за пасается энергия магнитного поля, электрического поля, происходят необратимые преобразования электромагнитной энергии в другие виды энергии. Эти явления учитывают элементы резистивный, индуктивный, емкостный.

Под цепями с распределенными параметрами понимают такие цепи, в которых энергии электрического и магнитного полей, а также необратимые преобразования энергии (потери в виде тепла) распределены равномерно или неравномерно вдоль цепи (ее длины).

К цепям с распределенными параметрами относят ЛЭП, линии телефонной связи, антенны приемно-передающих устройств. Обмотки электрических машин и трансформаторов тоже можно считать цепями с распределенными параметрами.

Рассмотрим двухпроводную однородную линию электропередачи. Однородной называют линию, параметры которой равномерно распределены вдоль ее длины. Это идеализированная линия, так как не учитывают изменение параметров от влияния провиса проводов и неравномерности поверхно-

сти земли.

В цепях с распределенными пара-

di

метрами напряжения и токи будут раз-

i

i + dx dx

личны на каждом участке и могут ме-

няться в пределах одного участка.

u

u +

du

dx

На рис. 11.1 изображен элементар-

dx

ный участок линии, у которого dx – дли-

на элементарного участка; i и u – ток и

x

dx

напряжение в начале участка;

Рис. 11.1

i + di dx

– ток в конце участка;

dx

u + du dx −напряжение в конце участка.

dx

Такой

элементарный

участок

обладает

параметрами:

C0dx, L0dx, R0dx, G0dx . C0 , L0 , R0 , G0 – первичные параметры однородной линии, т. е. параметры линии на единицу длины. Их считают обычно извест-

ными и постоянными: [R0 ]= Î ì /êì ; [G0 ]= Ñì /êì , [L0 ]= Ãí /êì , [Ñ0 ]= Ô/êì .

Элементарный участок с учетом первичных параметров представлен на рис. 11.2.

 Теоретические основы электротехники. Учеб. пособие

-281-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.1. Основные понятия

i

L0 dx R0 dx

u

C0 dx

G0 dx

dx

Рис. 11.2

Каждый участок линии длиной dx можно представить в виде Г- образного четырехполюсника, саму линию – в виде совокупности П- или Т-образных четырехполюсников, включенных последовательно.

Линию в целом можно рассматривать как симметричный четырехполюсник относительно входных и выходных зажимов.

11.2. Уравненияоднороднойлинии

Напряжение и ток линии зависят не только от времени, но и от пространственной координаты х (от точки линии): u(x, t); i(x, t).

Координату х можно отсчитывать от начала линии, конца или любой точки, принятой за начало отсчета. Начало линии – точка подключения линии к генератору, конец линии – точка подключения нагрузки к линии.

Будем вести отсчет координаты х от начала линии и считать, что вся нагрузка сосредоточена в конце линии, линия не имеет ответвлений.

Исследовать линию – это значит найти зависимости u(x, t) и i(x, t) в

любой точке линии в любой момент времени.

Определим изменение напряжения на участке dx, которое равно сумме падений напряжений на элементах этого участка:

					= − d u dx .
u − u + d u dx
		d x				d x
Из рис. 11.2 видно, что
− d u dx = (R dx) i +						(L dx)di .
d x		0				0	d t
Тогда
−	d u	= R		i + L		di .
	d x
			0			0 d t

Изменение тока в пределах этого участка равно сумме токов утечки в элементах этого участка:

− ddxi dx = (G0dx)u + (C0dx)ddut .

 Теоретические основы электротехники. Учеб. пособие

-282-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.2. Уравнения однородной линии

Отсюда

− ddix = G0u +C0 ddut .

Получим систему уравнений, которую называют телеграфными уравнениями однородной линии.

	− d u			= R i + L			di	;
		d x		0	0 d t
									(11.1)
		di		= G u +C			d u		.
−
		d x					d t
				0		0

Систему записывают с использованием частных производных, так как напряжения и токи зависят от двух координат: t и x.

Если за начало отсчета принять конец линии и координату до рассматриваемой точки линии обозначить х′, то получим систему уравнений, аналогичную системе(11.1), но в левой части знаки изменятся на противоположные:

d u				= R i + L			di ;
		d x′		0	0		d t
								(11.2)
di				= G u +C			d u	.
							d t
d x′				0		0

Решение системы (11.1) или (11.2) относительно напряжений и токов можно получить однозначно при известных начальных и граничных условиях.

Начальные условия – это значения токов и напряжений в начале или конце линии для момента времени t = 0.

Граничные условия устанавливают связь между напряжением и током в начале или конце линии в зависимости от режима работы линии.

11.3. Синусоидальныенапряженияитокивлинии

Если линия подключена к источнику синусоидального напряжения с частотой f, то напряжение и ток установившегося режима изменяются по синусоидальному закону с той же частотой.

В системе уравнений (11.1) перейдем от мгновенных значений к комплексным. Комплексные значения зависят от х и не зависят от t, так как ком-

плекс сопоставляют вектору в момент времени t = 0: I = I (x);U =U (x).

Поэтому получаем систему уравнений не в частных производных, а в обыкновенных (полных):

 Теоретические основы электротехники. Учеб. пособие

-283-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.3. Синусоидальные напряжения и токи в линии

	−dU = R I + jωL I = (R + jωL						)I = Z		I;
	d x		0	0	0	0	0
	− d I	= G U		+ jωC U	= (G	+ jωC ) U =Y U
											,
	d x		0	0	0	0				0

где Z 0 – комплексное продольное сопротивление на единицу длины линии; Y 0 – комплексная поперечная проводимость на единицу длины линии. Более краткая запись:

			= Z 0 I;
− dU
		d x
						(11.3)
		d I
	−
			=Y U.
		d x			0

Из системы уравнений (11.3), исключая либо ток, либо напряжение, можно получить соответственно дифференциальное уравнение для напряжения или тока.

Продифференцировав первое уравнение и подставив в него значение

d I из второго, получим: d x

d2U = Z 0Y 0U . d x2

Обозначим 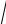Z 0Y 0 = 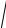(R0 + jωL0 )(G0 + jωC0 ) = γ – коэффициент рас-

пространения.

Тогда уравнение примет вид

2	2
d U		(11.4)
d x2	− γ U = 0.

Как известно из математики, решение этого уравнения есть сумма двух экспоненциальных функций:

		−γx		γx	,	(11.5)
U = A e			+ A e
	1		2

где U – комплекс действующего значения напряжения для любой точки линии; А1 и А2 – постоянные интегрирования;

 Теоретические основы электротехники. Учеб. пособие

-284-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.3.Синусоидальные напряжения и токи в линии

γи −γ – корни характеристического уравнения, получаемого из (11.4):

p2 − γ2 = 0 . Отсюда p = ±γ.

Аналогично можно получить решение для тока:

dd2xI2 = Z 0Y 0 I .

Но такое решение нецелесообразно, так как нужно искать еще две постоянные интегрирования.

Более рационально найти ток из первого уравнения системы (11.3):

I = −

1 dU

= −

1 d

(A1 e−γx + A2 eγx )=

Z 0 d x

Z 0

d x

γ

(A1

γx )

=

e−γx − A2 e

=

Y

0

(A1e−γx − A2 eγx ).

(11.6)

Z 0

Z 0

Комплексное выражение

Z 0

зависит от первичных параметров и

Y

0

имеет размерность сопротивления.

Его называют характеристическим или волновым сопротивлением линии и обозначают Z ñ :

Z ñ = Zc e jθ =		R0 + jωL0		.
		G0 + jωC0

Тогда комплекс действующего значения тока для любой точки линии можно записать следующим образом:

I =	A1	e−γx −	A2	eγx .
	Z c		Z c

Для выяснения физического смысла слагаемых напряжения в уравнении (11.5) перейдем к мгновенному значению напряжения u (x, t). При этом

учтем, что постоянные интегрирования и коэффициент распространения являются комплексными числами:

A1 = A1e jψ1 ; A2 = A2e jψ2 ;

 Теоретические основы электротехники. Учеб. пособие

-285-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.3. Синусоидальные напряжения и токи в линии

γ = 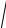(R0 + jωL0 )(G0 + jωC0 ) = α+ jβ,

где α – коэффициент затухания, характеризующий степень убывания амплитуды;

β – коэффициент фазы, характеризующий изменение фазы.

Мгновенное значение напряжения	u (x, t)= A	e−αx sin (ωt −βx + ψ )+
	1m	1

+A2meαx sin (ωt +βx + ψ2 ).

Если считать координату х фиксированной, то первое слагаемое изменяется по синусоидальному закону с постоянной амплитудой напряжения.

Если считать фиксированным время, то напряжение меняется по синусоиде, затухающей по экспоненте.

Убывание амплитуды волны вдоль линии обусловлено потерями в линии, а изменение фазы – конечной скоростью распространения электромагнитных колебаний.

Коэффициенты α è β, входящие в γ, характеризуют распространение волны вдоль линии, поэтому γ назвали коэффициентом распространения.

u

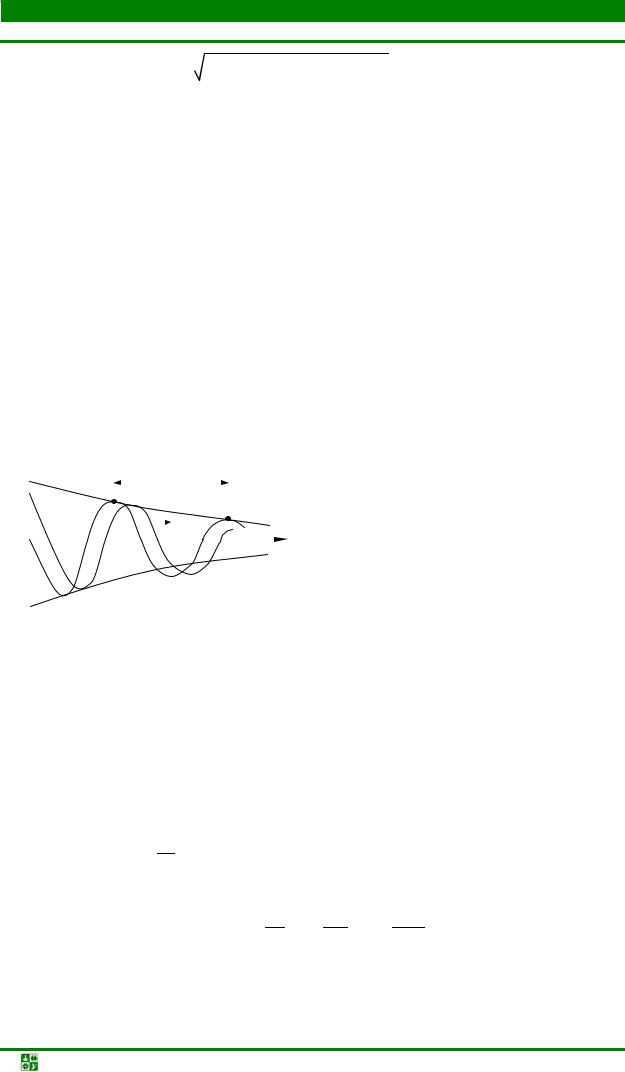
На рис. 11.3 приведены вол-

А1m e -αx

λ

ны напряжения для двух моментов

t2

времени t1 и t2 (t2 > t1).

υ

x

Волна перемещается от на-

чала линии к концу с постоянной

скоростью υ.

t1

–А1m e -αx

Любое колебательное дви-

жение характеризуют фазовой ско-

Рис. 11.3

ростью и длиной волны.

Фазовая скорость – это ско-

рость изменения фазы колебания, которая с течением времени и ростом координаты х остается неизменной:

(ωt −βx + ψ1 ) = const .

Исследуем это выражение на экстремум:

ddt (ωt −βx + ψ1 ) = ωddtt −βddxt + ddψt1 = 0 .

В полученном выражении ddtt =1, ddxt = υ, ddψt1 = 0 .

 Теоретические основы электротехники. Учеб. пособие

-286-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.3. Синусоидальные напряжения и токи в линии

Тогда υ = ωβ .

Если в воздушной линии пренебречь потерями, то максимальная фазовая скорость примерно равна скорости света:

υ ≈ ñ = 3 105 êì /ñ.

Длина волны λ – это кратчайшее расстояние между двумя точками, взятое в направлении распространения волны, фаза колебания которых отличается на 2π (см. рис. 11.3).

Следовательно, для первого слагаемого напряжения с учетом, что фазу откладываем в направлении волны влево, можно записать:

ωt −β(x + λ)+ ψ1 = ωt −βx + ψ1 − 2π.

Отсюда λ = 2βπ .

Фазовая скорость

υ = ωβ = 2βπf = λf = Tλ .

Отсюда следует, что за время, равное одному периоду, волна пробегает расстояние, равное длине волны.

Первая составляющая напряжения имеет максимальную амплитуду в начале линии и минимальную в конце. Эта составляющая напряжения движется от начала линии к концу со скоростью υ. Эту волну называют бегущей (прямой или падающей составляющей).

Так как второе слагаемое имеет амплитуду A2meαx (со знаком плюс), то она достигает максимального значения в конце линии. Эту волну называют

	u		А2m eαx		обратной или отраженной.
					В фазе колебания второе сла-
	–υ		t1		гаемое βx	– со знаком плюс, поэтому
				x	фазовая скорость υ = − ω .
						β
			t2
					Это означает, что вторая со-
					ставляющая напряжения перемещает-
			–А2m eαx		ся с той же скоростью, что и первая,
	Рис. 11.4				но от	конца линии к началу
					(рис. 11.4).

 Теоретические основы электротехники. Учеб. пособие

-287-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.3. Синусоидальные напряжения и токи в линии

Напряжение u(x,t) имеет положительное направление от верхнего

(первого) провода к нижнему (второму) и состоит из суммы двух составляющих с такими же положительными направлениями:

u(x,t) = uпр(x,t) + uобр(x,t) .

Аналогично можно получить мгновенное значение тока:

i(x,t) = A1m = e−αx sin(ωt −βx + ψ1 − θ) −

Zc

−A2m eαx sin(ωt +βx + ψ2 − θ) = iï ð (x,t) −iî áð (x,t).

Zc

Результирующий ток и его прямая составляющая совпадают по направлению и направлены от начала к концу линии, обратная составляющая направлена от конца к началу линии.

Коэффициентом пропорциональности между Um и Im , U и I прямой и

обратной волны является характеристическое (волновое) сопротивление каждой волны.

В комплексной форме можно записать:

U	ï ð.	= Z c ;	U	î áð.	= Z c .
Iï ð.			Iî áð.

Напряжение и ток сдвинуты относительно друг друга по фазе на уголθ. Мощности в цепях с распределенными параметрами для каждой волны

определяют так же, как в цепях с сосредоточенными параметрами. Например, комплексная мощность прямой волны

*

Sï ð =Uï ð I ï ð = Ðï ð + jQï ð =Uï ð Iï ð cosθ+ jUï ð Iï ð sin θ.

Активная мощность прямой волны

Ðï ð = Rc Iï2ð = Uï2ð .

Rc

Представление напряжений и токов в виде прямой и обратной составляющих есть математический прием, который облегчает анализ таких цепей. Реально в цепях с распределенными параметрами существуют результирующие напряжения и токи.

 Теоретические основы электротехники. Учеб. пособие

-288-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.4. Вторичныепараметрыоднороднойлинии

Однородную линию можно характеризовать с помощью двух параметров: коэффициента распространения

γ = 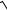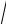Z 0Y 0 = 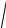(R0 + jL0ω)(G0 + jC0ω) = α+ jβ

и волнового (характеристического) сопротивления

(R0 + jL0ω)

Z

=

Z 0

=

= Z

e jθ .

c

(G + jC ω)

Y

0

c

0

0

Они зависят от первичных параметров R0 , L0 , G0 , C0 и частоты. Опре-

делим зависимость этих параметров от частоты. Коэффициент распространения

α + Jβ = 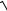(R0 + jL0ω)(G0 + jC0ω) = 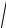R0G0 − ω2 L0C0 + jω(G0L0 + R0C0 ).

Выделим вещественную и мнимую части. Для этого возведем обе части равенства в квадрат:

α2 + j2αβ −β2 = R0G0 − ω2 L0C0 + jω(G0L0 + R0C0 ).

Для действительных составляющих получим уравнение

			α2 −β2 = R G − ω2 L C ,
			0	0	0	0
для мнимых			2αβ = ω(G0L0 + R0C0 ).
Совместное решение этих уравнений относительно α и β дает:
α =	1	R0G0	− ω L0C0 +							;
				(R0	+ ω L0 )(G0		+ ω C0	)
			2	2	2 2	2	2 2
	2
β =	1	ω L0C0 − R0G0 +							.
				(R0	+ ω L0 )(G0		+ ω C0	)
		2		2	2 2	2	2 2
	2

Построим зависимости коэффициентов α и β от частоты, считая, что первичные параметры от частоты не зависят.

Когда ω = 0 , коэффициент затухания α(0) = R0G0 .

 Теоретические основы электротехники. Учеб. пособие

-289-

	ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
		11.4. Вторичные параметры однородной линии
	Когда ω = ∞, коэффициент затухания α(∞) =						R0	C0	+ G0	L0 .
							2	L	2	C
								0		0
	Первое слагаемое обусловливает затухание амплитуды волны из-за
продольного активного сопротивления линии.
	Второе слагаемое обусловливает затухание волны за счет поперечной
активной проводимости.
	Для уменьшения затухания R0 и G0				необходимо уменьшить.
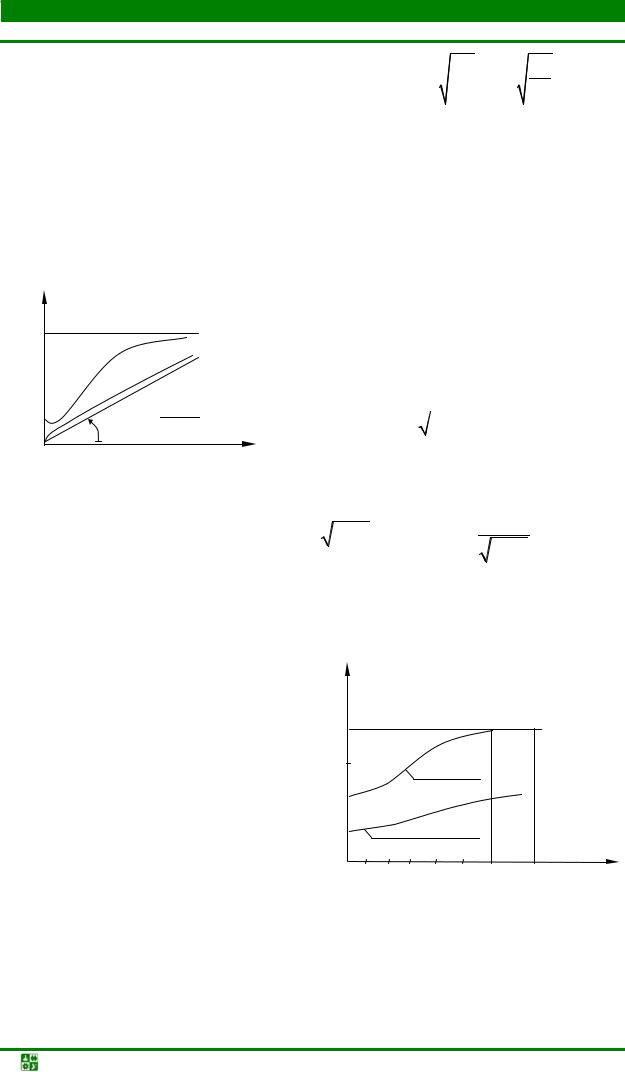
	Графики зависимостей α(ω) и β(ω)				представлены на рис. 11.5.
					При частоте ω = 0 коэффициент
α; β				затухания β = 0 .
					При увеличении частоты ω ко-
α∞				эффициент			β	меняется		нелинейно
	α	β		(β нелинейно зависит от частоты). При
				ω→ ∞ график β(ω)					стремится к пря-
α0				мой,	направленной к оси абсцисс под
		arctq √ L0C0 m		углом àrctg m L0C0					(m –	масштабный
			ω
		Рис. 11.5		коэффициент).						υ = ω.
					Фазовая			скорость			При
										β
ω→ ∞ коэффициент затухания				β = ω L C		. Тогда		υ =	1	, т. е. при
					0	0			L0C0
ω→ ∞ фазовая скорость от частоты не зависит.
	Фазовая скорость зависит от материала. Графики зависимости υ( f )
приведены на рис. 11.6.
	Зависимости α(ω), β(ω) , υ(ω) имеют большое практическое значение.

В линиях передачи информации сигнал несинусоидальной формы и при передаче сигнала его гармонические составляющие перемещаются вдоль линии с разной скоростью и затухают по-разному, т. е. на выходе л и- нии получают искаженный сигнал. Поэтому в линиях передачи информации необходимо принимать меры для устранения искажения сигнала.

Характеристическое сопротивление

υ 105

3

2 медные

1

стальные

f

20

40

80

160 370

640

1280

Гц

Рис. 11.6

 Теоретические основы электротехники. Учеб. пособие

-290-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
11.4. Вторичные параметры однородной линии
Z c =	(R0 + jL0ω)		= Zce jθ .
	(G0 + jC0ω)
При ω = 0 сопротивление Zc (0) =		R0	, т. е. имеет активный характер.
		G0
При ω = ∞ сопротивление Zc (∞) =		L0 , т. е. также имеет активный ха-
рактер.		C0
			zC ; θ
В остальном интервале	частот Z c
имеет емкостный характер, так как аргумент			zC0	zC
знаменателя больше аргумента числителя.					√ L0	/C0
На рис. 11.7 представлены кривые			zC∞			ω
зависимости полного волнового сопро-
				θ
тивления и угла θ от частоты.
Волновое сопротивление возрастает
при уменьшении диаметра проводов		и		Рис. 11.7
увеличении расстояния между проводами.
Для воздушной линии электропередачи Zc =(300–600) Ом, для кабеля
Zc =(50–200) Ом.
11.5. Зависимостьрежимаработылинииотнагрузки

Пусть в начале линии длиной l (рис. 11.8) включен генератор, напряжение на зажимах которого U1, а в конце линии – приемник с сопротивлени-

ем Z í = Zí e jϕí .

I	Rг	1			2	I2
1
Ег		U1			U2	Zн
		1	х	х	2
			l
			Рис. 11.8

Нужно определить напряжение U1 , необходимое для создания на нагрузке заданного напряжения U2 . Одновременно вычислим ток генератора I1

 Теоретические основы электротехники. Учеб. пособие

-291-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.5.Зависимость режима работы линии от нагрузки

ираспределение тока и напряжения вдоль линии.

По закону Ома ток

I2 = U2 .

Z í

Напряжение и ток на расстоянии х от начала линии:

	U	= A				e−γ x + A			e−γ x ;
				1			2
			A1				A2
	I =					e−γ x −			e−γ x .
			Z	c			Z	c

Заменим в этих уравнениях х на (l − x′), т. е. перенесем начало отсчета координаты х из начала линии в конец:

	U	= A					e−γ(l−x) + A			eγ(l −x′) ;
					1				2
			A1					A2
I =						e−γ(l−x′) −				e−γ(l−x′) .
			Z	c				Z	c

Обозначим A1e−γl = B1 ,

A2eγl = B2 ,

где B1 и B2 – новые постоянные интегрирования.

Тогда вместо x′ можно писать х без штриха, так как отсчет координаты х от начала или конца линии определяют по заданному режиму. Получим уравнения

γx

−γx

;

U

= B e

+ B e

B

1

2

γx

B

−γx

I =

1

e

−

2

e

.

Z c

Z c

Для конца линии (x = 0, U =U2 , I = I2 )

 Теоретические основы электротехники. Учеб. пособие

-292-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.5. Зависимость режима работы линии от нагрузки

U		2	= B				+ B			;
					1			2
				B1				B2
I2		=		Z	c		−	Z	c	;

I2 Z c = B1 − B2 .

Отсюда

B	=	U2 + Z c I2	;	B	=	U2 − Z c I2	.
1	2			2	2

Следовательно, напряжение в линии

U =

U2 + Z c I2

eγx +

U2 − Z c I2

e−γx =

2

2

eγx + e−γx

eγx −e−γx

=U2

2

+ Z c I2

2

=U2

ñhγx + Z c I2shγx .

Аналогичное уравнение можно получить и для тока:

I = I2ch γ x + U2 sh γ x .

Z c

Полученные уравнения позволяют определить напряжение и ток в любой точке линии при заданном режиме в конце линии.

Приняв x = l , получим уравнения линии в гиперболической форме, выражающие напряжение и ток в начале линии через напряжение и ток в конце линии:

	U1 =U2 ñh γl + Z c I2 sh γl;
			U
		I1 = I2 ch γl +		2	sh γ l.
			Z c

Если отсчет координат х будем проводить от начала линии, при заданных U1 и I1 и x = 0 получим уравнения:

 Теоретические основы электротехники. Учеб. пособие

-293-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.5. Зависимость режима работы линии от нагрузки

U	1	= A		+ A		;
			1		2
I1		=	A1	−	A2		.
			Z c
					Z c

Из второго уравнения

						Z	I	= A		− A	.
							c 1	1		2
Отсюда A	=	U1 + Z c I1	;	A	=	U1 − Z c I1			.
1	2			2	2

Подставив постоянные интегрирования, получим уравнения:

U =

U1 + Z c I1

e−γx

+

U1 − Z c I1

eγx

=U1 ch γ x − Z c I1 sh γ x ;

2

2

I =

U1 + Z c I1

e−γx −

U1 − Z c I1

eγx = I1 ch γ x −

U1

sh γ x .

2Z c

2Z c

Z c

Сведем их в систему

U

=U1 ch γ x − Z c I1 sh γ x;

U

1

I = I1 ch γ x −

sh γ x.

Z c

Эта система позволяет определить напряжение и ток в любой точке линии, если задан режим работы на входе линии.

Если линия электропередачи работает на постоянном токе, т. е. ω = 0 , то между проводами линии и внутри проводов существуют постоянные магнитное и электрическое поля. ЭДС самоиндукции отсутствует, токи утечки между проводами отсутствуют.

Напряжение и токи совпадают по фазе. Характеристические параметры

являются действительными числами.						γ = α+ jβ. Коэффициент фазы β = 0 ,
Коэффициент распространения
поэтому γ = α =		.
	R0G0
Волновое сопротивление Z			c	= Z	c	=		R0		= R .
										c
								G0

Расчеты проводят для действующих значений электрических величин. При заданном режиме в конце линии система уравнений, позволяющая

рассчитать напряжение и ток в любой точке, примет вид

 Теоретические основы электротехники. Учеб. пособие

-294-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.5. Зависимость режима работы линии от нагрузки

	U =U2 ch αx + Rc I2 sh αx;
			U
		I = I2 ch αx +		2	sh αx.
			Rc

11.6.Согласованнаяинесогласованнаянагрузка

Воднородной линии обратная волна существует в случае, если нагрузка линии не согласована с ее характеристическим сопротивлением:Z í ≠ Z c .

Отношение комплекса напряжения (тока) обратной волны в конце линии к комплексу напряжения (тока) прямой волны в конце линии называют коэффициентом отражения.

Так

как

U

(0) = B ;

U

(0) = B ,

то

n =

Uî áð (0)

=

B

=

2

U

(0)

î áð

2

ï ð

1

ï ð

B

1

=

U

2

− Z

I

=

Z

í

− Z

c

. Коэффициент отражения линии зависит от соотноше-

c 2

Z í + Z c

U2

+ Z c I2

ния сопротивления нагрузки и характеристического сопротивления. Наибольшие значения коэффициент отражения принимает в режимах холостого хода и короткого замыкания в конце линии.

В режиме холостого хода Z í = ∞, n =1, в режиме короткого замык а-

ния n = −1, что означает полное отражение.

Чем больше по модулю коэффициент отражения, тем более неравномерно вдоль линии распределены действующие значения напряжения и тока. При несогласованной нагрузке часть энергии в виде отраженной составляющей возвращается источнику.

При передаче сигналов и информации, как правило, подбирают согласованный режим. В этом случае n = 0, отраженная волна отсутствует. В со-

гласованном режиме Z í

= Z ñ . По закону Ома U2

= Z c I2.

Тогда B2

=

1

− Z c I2 )= 0 ; Uî áð = B2e

−γx

B

−γx

= 0.

2 (U2

= 0; Iî áð = Z c e

2

Уравнения линии принимают вид

U

=Uï ð = B1eγx =

U2

+ Z c I2

eγx =U2e

γx ;

2

B1

U2

+ Z c I2

I

= Iï ð =

eγx =

eγx = I2eγx .

Z c

2Z c

Действующие значения напряжения и тока вдоль линии при согласованной нагрузке изменяются по экспоненте (рис. 11.9).

Вся энергия, поступающая в нагрузку, полностью ею потребляется. При несогласованной нагрузке отраженная волна возвращается в начало ли-

 Теоретические основы электротехники. Учеб. пособие

-295-

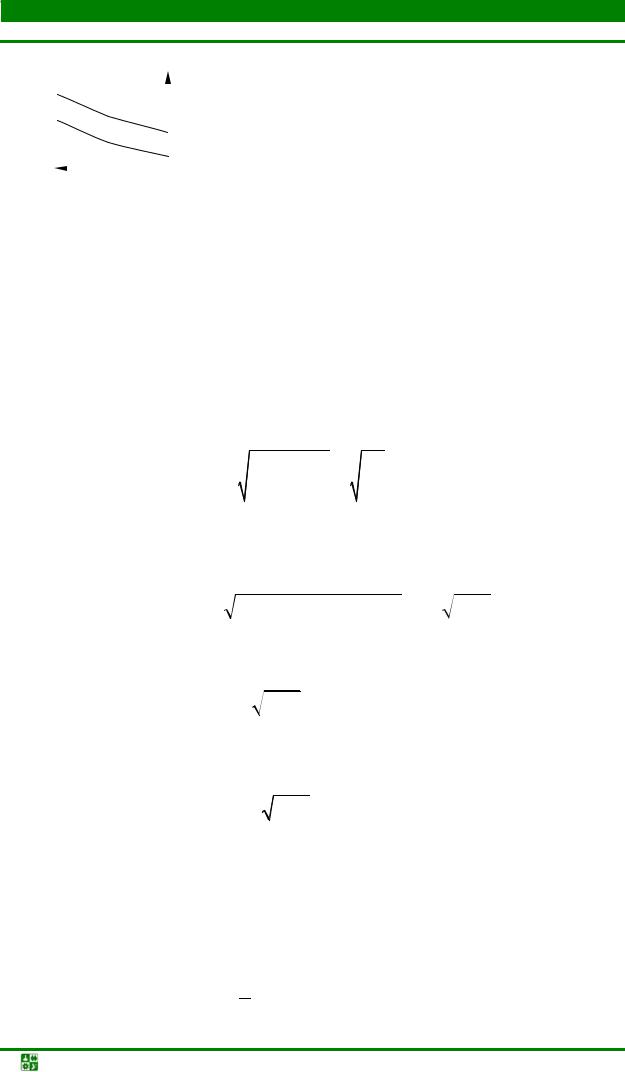
ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.6. Согласованная и несогласованная нагрузка

	U, I
I2 eαx	U2 eαx		U2
x			I2
		0
	Рис. 11.9

нии. Если сопротивление генератора не равно Z c ,

то происходит повторное отражение и вновь отраженный сигнал поступает в нагрузку, для которой он является ложным. В линиях телефонной связи это приводит к неразборчивости речи, а в телевизионных приемниках – к нечеткости и мно-

гоконтурности изображения.

11.7.Линиибезпотерь

Влиниях, соединяющих приемно-передающую аппаратуру с антеннами, потери много меньше мощности, потребляемой нагрузкой. Этими потерями пренебрегают и такую линию считают линией без потерь, принимают

R0 = 0 и G0 = 0 .

У линии без потерь волновое сопротивление чисто активное и не зависит от частоты:

Z c =		R0 + jωL0		=		L0		= Zc .
		G0 + jC0ω
						C0

Угол θ = 0 . Это означает что напряжение и ток прямой и обратной волн совпадают по фазе.

Коэффициент распространения

γ = α+ jβ = 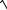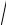(R0 + jl0ω)(G0 + jC0ω = jω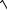L0C0 .

Отсюда следует, что коэффициент затухания α = 0. Линия без потерь – линия без затухания.

Коэффициент фазы β = ω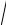L0C0 прямо пропорционален частоте.

Так как γ = jβ, то и коэффициент распространения прямо пропорцио-

нален частоте.	ω			1
Фазовая скорость υ =		=				. Фазовая скорость в линии без потерь
	β
				L0C0

не зависит от частоты. Однородная линия без потерь – это линия без искажений.

Уравнения однородной линии с гиперболическими функциями от комплексного аргумента заменяют для линии без потерь уравнениями с круговыми функциями от вещественного аргумента.

Так как

ch γ x = ch jβx = cosβx ;

 Теоретические основы электротехники. Учеб. пособие

-296-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.7. Линии без потерь

sh γ x = sh jβx = jsinβx ; Z ñ = Zc , уравнения примут вид

	U =U2 cosβx + jZñI2 sinβx;
			U
		I = I2 cosβx + j		2	sin βx.
			Zc

В случае несогласованной нагрузки есть прямая и обратная составляющие напряжения и тока. Амплитуда каждой составляющей вдоль линии остается постоянной (α = 0). Результирующие действующие значения на-

пряжения и тока вдоль линии распределены неравномерно.

11.8. Согласованнаянагрузкалиниибезпотерь

При согласованной активной нагрузке

	Z í	= Z ñ = Zc =		L0		; U2 = Zc I2 ,
				C0
								j β x		;
U =U2 cosβx + jU2 sinβx =U2e
							j β x		.
	I	= I2 cosβx + j I2 sinβx = I2e

Примем, что начальная фаза напряжения в конце линии равна нулю. Тогда мгновенные значения напряжения и тока следующие:

		u(x, t) =U2msin(ωt +βx) ;
		i(x, t) = I2msin(ωt +βx) .
		u;i			Напряжение и ток вдоль линии
					изменяются по синусоидальному за-
				U2m	кону с постоянной амплитудой и сов-
				I2m	падают по фазе (рис. 11.10).
х					Отраженной волны нет. Дейст-
	х2	х1			вующие значения напряжения и тока не
					зависят от координаты х (рис. 11.11).
					Мощность волны, движущейся от ге-
	Рис. 11.10				нератора к приемнику, полностью по-
					глощается нагрузкой.

 Теоретические основы электротехники. Учеб. пособие

-297-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.8. Согласованная нагрузка линии без потерь

P =UI = Zc I

2 = U 2 .

Zc

U, I

Волновое сопротивление Zc =

U

L0

U

=

=

. После возведения в квадрат полу-

I

C0

I

U 2

L0

. Отсюда L I 2 = C U 2 .

чим

=

Энергия

х

I 2

C0

0

0

Рис. 11.11

магнитного

поля катушки

L

I 2

0

,

энергия

2

электрического поля конденсатора

C U 2

L I 2

C U 2

0

. Очевидно, что

0

=

0

.

2

2

2

Следовательно, энергия распределяется поровну между электрическим и магнитным полями между проводами линий.

11.9. Входноесопротивлениелинии

Входное сопротивление линии – это входное сопротивление двухполюсника, который необходимо подключить к зажимам генератора вместо линии, чтобы режим работы генератора остался без изменения.

При известных напряжении и токе генератора система уравнений линии:

U1 =U2ch γl + Z c I2 sh γl =U2 (ch γl +

Z

c

sh γl);

Z í

1

I1 = I2 ch γl +

U2

shγl =U

2

1

sh γl +

sh γl .

Z c

Z í

Z í

Входное сопротивление равно отношению входного напряжения к входному току:

						Z
	U			ch γl +			c	sh γl
Z âõ =						Z
	1	=				í				.
				1		1
	I1								sh γl
				Z í	ch γl + Z c

Разделив на ch γl , получим:

	Z âõ = Z ñ	Z í + Z c th γl	.	(11.7)
		Z c + Z í th γl

 Теоретические основы электротехники. Учеб. пособие

-298-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.9. Входное сопротивление линии

Отсюда видно, что входное сопротивление линии зависит от ее параметров, длины, частоты, сопротивления нагрузки в конце линии.

Выясним зависимость входного сопротивления линии от ее длины и частоты.

Для этого обозначим	Z í = th M , где M – комплексное число;
	Z c
	M = m1 + j m2 .
Разделив выражение входного сопротивления на Z c , получим

Z âõ = Z ñ

th M +th γl

= Z c th(γl + M ) = Z c th[(αl + m1 )(βl + m2 )]. (11.8)

1+th M th γl

Но Z

âõ

= Z

âõ

e jϕâõ = R

+ j x

âõ

= Z

âõ

cosϕ

âõ

+ j Z

âõ

sin ϕ

âõ

.

âõ

Отсюда следует, что увеличение длины линии l изменяет как полное сопротивление Zвх , так и аргумент ϕâõ входного сопротивления линии.

Выражение (11.8) удобно использовать для анализа зависимости входного сопротивления от длины линии l или от частоты f.

При заданных параметрах линии и сопротивления нагрузки проще пользоваться выражением (11.7).

Если задан коэффициент отражения n , то Z âõ можно выразить через него:

1−

Z

U

− Z

I

Z

− Z

c

n =

Z

2

c 2

=

í

c

=

í

.

Z

U2

+ Z c I2

Z í

+ Z c

1+

c

Отсюда

Z í

Z c

1

− n .

=

(11.9)

Z í

1

+ n

Гиперболический тангенс

th γl = eγll −e−γll .

eγ + e−γ

Умножив на e−γl , получим:

th γl = 1−e−2γll . 1+ e−2γ

 Теоретические основы электротехники. Учеб. пособие

-299-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.9. Входное сопротивление линии

Отсюда 1−e−2γl = (1+ e−2γl )th γl ;

e−2γl = 1l −+ thth γγll . (11.10)

Подставив выражение (11.9) в (11.7) и с учетом (11.10), получим:

Z		= Z		1+ n e−2γl	.
	âõ		ñ 1− n e−2γl

При коротком замыкании (Z н = 0) из выражения (11.7)

Z âõ = Z êç = Z cthγl .

(11.11)

При холостом ходе (Z н = ∞)

Z âõ = Z õõ = Z c cth γl .

(11.12)

Если известны Z кз и Z хх , входное сопротивление линии можно выразить через эти параметры. Подставив (11.11) и (11.12) в (11.7), получим:

Z вх = Z хх	Z н + Z кз	.
	Z н + Z хх

Сопротивления Z хх и Z кз легко определить опытным путем. Их и с-

пользуют для вычисления вторичных параметров линии.

Волновое сопротивление получим, умножив выражение (11.11) на выражение (11.12):

Z ñ = 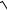Z êç Z õõ .

Разделив выражение (11.11) на (11.12), получим:

th γl =		Z êç		.
		Z õõ

Отсюда можно вычислить коэффициент распространения.

 Теоретические основы электротехники. Учеб. пособие

-300-

ГЛАВА 11. ЦЕПИ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ

11.9. Входное сопротивление линии

Входное сопротивление линии без потерь при согласованном режиме

Zí + jZc tgβl	1+ n e− j 2βl
Z âõ = Zñ Zc + jZí tgβl	= Zc 1− n e− j 2βl .

Так как коэффициент отражения n = 0, то Z âõ = Zñ , т. е. является чисто активным для любой длины линии.

 Теоретические основы электротехники. Учеб. пособие

-301-