9. Деформируемое твердое тело
2. На две вертикальные плоские ферм АА' и BB' с нагрузкой от собственного веса и веса поезда (рис. 9.3, б). На горизонтальную ферму с нагрузкой от давления ветра (рис. 9.3, в).
9.2. Классификация нагрузок
Внешними силами, или нагрузками, называют силы воздействия рассматриваемого элемента конструкции на связанные с ним тела. Имеются различные способы приложения нагрузок. Для большинства целей достаточно их различать по характеру распределения сил и характеру действия сил.
К нагрузкам, различаемым по характеру распределения сил, относятся объемные нагрузки, поверхностные нагрузки, погонные нагрузки и сосредоточенные силы.
Объемные нагрузки – нагрузки, приложенные ко всем частицам объема рассматриваемого тела (собственный вес, силы инерции).
Интенсивность объемных нагрузок = ОбъемCила , измеряется в Н/м3.
Поверхностные нагрузки – нагрузки, распределенные по поверхности, например, давление, передаваемое жидкостью на стенки сосудов.
Интенсивность поверхностных нагрузок = ПлощадьCила , измеряется
в Н/м2.
Погонные нагрузки – нагрузки, распределенные на протяжении длины, например, собственный вес стержня, распределенный по ее длине.
Интенсивность распределенной нагрузки = ДлинаСила , измеряется
в Н/м.
Сосредоточенные силы рассматриваются приложенными к точке. Это приближенное представление силы, передаваемой через площадку, размерыкотороймалыпосравнениюсрасстояниемдоэтойплощадки.
Интенсивность сосредоточенной силы = Сила, измеряется в Н. К нагрузкам, различаемым по характеру действия сил, относятся
непродолжительные и продолжительные статические нагрузки, повторные и динамические нагрузки.
185
И. В. Богомаз. Механика
Внутренние силы – результат действия одних частей тела на другие. Они существуют и при отсутствии внешних силовых воздействий как результат взаимодействия между частицами тела. Но под действием внешних сил в материале возникают дополнительные внутренние силы, сопровождающие деформацию. Эти силы и определяются в задачах сопротивления материалов. Для определения внутренних сил применяется метод сечений.
9.3. Метод сечений. Виды сопротивлений бруса. Построение эпюр
Пусть на брус действует система взаимно уравновешенных внешних сил F1, F2 … Fn (рис. 9.4, а). Для определения внутренних сил производят последовательно четыре операции:
1.Рассекают брус воображаемой плоскостью на две части
(9.4, б).
2.Отбрасывают мысленно одну из образовавшихся частей (например, часть I).
3.Заменяют действие отброшенной части I на оставшуюся II внутренними силами fi (рис. 9.4, б). При этом имеют в виду, что внут-
ренние силы могут быть приведены к центру тяжести сечения
итаким образом заменены главным вектором R и главным моментом
М(рис. 9.4, в). Каждый из этих двух статических эквивалентов внутренних сил можно разложить по осям выбранных координат Oxyz. Направим ось Oz по нормали n к сечению, оси Ox и Oy расположим в плоскости сечения (рис. 9.4, г). Получим три проекции главного вектора и три проекции главного момента, которые соответствуют:
• N − продольной силе (проекция главного вектора R ось Oz);
•Qx, Qy − поперечным силам (проекция главного вектора R на оси Ox и Oy соответственно);
•Mz − крутящему моменту (проекция главного момента М на ось Oz);
•Mx, My − изгибающим моментам (проекция главного момента
Мна оси Ox и Oy соответственно).
Эти проекции главного вектора и главного момента называются внутренними силовыми факторами или внутренними усилиями.
186
9. Деформируемое твердое тело
Рис. 9.4
Эти шесть усилий совместно с внешними силами, действующими на отсеченную часть бруса, должны обеспечить равновесие этой части (II). Таким образом, для каждой части бруса должны быть выполнены шесть условий равновесия для вычисления внутренних силовых факторов (табл. 9.1).
|
|
Таблица 9.1 |
|
|
|
|
|
Уравнение |
Внутренний силовой |
Вид сопротивления бруса |
|
равновесия |
фактор |
||
|
|||
∑Fzi = 0 |
n |
|
|
N = ∑Fz (Fi ) отс.ч |
Растяжение или сжатие |
||
|
i=1 |
|
|
∑Fxi = 0 |
n |
|
|
Qx = ∑Fx (Fi ) отс.ч |
Сдвиг |
||
|
i=1 |
|
|
∑Fyi = 0 |
n |
|
|
Qy = ∑Fy (Fi ) отс.ч |
Сдвиг |
||
|
i=1 |
|
|
∑mzi = 0 |
n |
|
|
M z = ∑m z(Fi )отс.ч |
Кручение |
||
|
i=1 |
|
|
∑mxi = 0 |
n |
|
|
M x = ∑m x(Fi )отс.ч |
Изгиб в плоскости Oyz |
||
|
i=1 |
|
|
∑myi = 0 |
n |
|
|
M y = ∑m y(Fi )отс.ч |
Изгиб в плоскости Oxz |
||
|
i=1 |
|
|
|
|
187 |
И. В. Богомаз. Механика
Вычисляя внутренние усилия, нужно иметь в виду следующее:
•продольная сила N численно равна алгебраической сумме
проекций на продольную ось z всех внешних сил, действующих на отсеченную часть: Qx на ось x , Qy на ось y соответственно;
•изгибающие моменты Mx относительно оси x и My относительно оси y численно равны алгебраической сумме моментов всех внешних сил относительно поперечных осей, действующих на отсеченную часть;
•крутящий момент Mz численно равен алгебраической сумме моментов всех внешних сил относительно продольной оси z, действующих на отсеченную часть.
Принято порядок действий метода сечений называть правилом РОЗУ (аббревиатура из первых букв выделенных слов).
Р− рассекают; О − отбрасывают; З − заменяют; У − уравновешивают.
Отметим, что согласно третьему закону Ньютона совершенно безразлично, равновесие какой отсеченной части рассматривать, так как внутренние силовые факторы (внутренние усилия), приложенные к обеим отсеченным частям, равны по модулю и противоположны по знаку, т. е. взаимны.
Таким образом, метод сечений позволяет вычислить все внутренние усилия и моменты в любом сечении бруса при действии любой нагрузки.
При различных комбинациях простых видов нагружений (сжатие с изгибом, изгиб с кручением и др.) возникает сложное сопротивление (нагружение) бруса.
Каждую отсеченную часть обычно изображают отдельно и рядом с этим рисунком записывают уравнения ее равновесия. Такая технология обеспечивает наглядность, простоту работы, а значит, и надежность результатов. Внутренние силы – это векторы, как и любые силы.
Графики, показывающие, как изменяются внутренние силовые факторы (усилия) вдоль оси бруса, называются эпюрами.
Для расчетов на прочность и жесткость очень важно уметь определять положение опасных сечений, т. е. важно знать координаты положения сечений zi, в которых величины внутренних силовых факторов максимальны. Эпюра дает наглядное представление об изменении внутреннего силового фактора (усилия) по длине бруса.
188
9. Деформируемое твердое тело
При построении эпюр рекомендуется придерживаться следующего порядка:
1.Выявляют все внешние силы, действующие на брус (реакции опор в том числе).
2.Разбивают брус на участки, в пределах которых одинаково нагружение бруса, а внутренние усилия изменяются по одной закономерности.
Участком называется часть стержня между сосредоточенными нагрузками M, F или часть стержня, в пределах которого распределенная нагрузка q меняется по одному закону.
3.На каждом участке проводят произвольное сечение и фиксируют его абсциссой zi (рис. 9.5).
4.Применяя метод сечений, для каждого участка составляют
выражения для внутренних сил N(z), Qx(z), Qy(z) и моментов Mz(z), Mx(z), My(z) как алгебраические суммы соответствующих проекций
имоментов внешних сил, действующих на одну из частей (левую или правую по отношению к сечению).
5.Меняя значение координаты z, вычисляют внутренние усилия на границах участков и в характерных сечениях.
6.Параллельно оси бруса проводят ось (базу), на которой строят
эпюру.
7.Ординаты эпюры, выражающие в выбранном масштабе значения силы или момента, откладывают от базы по перпендикуляру.
8.В поле эпюры ставят знак усилия в кружочке и наносят штриховку линиями, перпендикулярными к базе, проставляют числа, показывающие величины характерных ординат.
Рис. 9.5
189
И. В. Богомаз. Механика
Эпюры внутренних усилий, как правило, строят для того, чтобы выявить опасные сечения, т. е. сечения, в которых существует большая вероятность разрушения из-за того, что там внутренние усилия достигают наибольших значений.
Построение эпюр продольных сил N при растяжении (сжа-
тии) бруса. При растяжении (сжатии) бруса все внешние силы действуют вдоль оси бруса z. В этом случае в поперечных сечениях бруса возникает только одно внутреннее усилие – продольная сила N(z) (рис. 9.6, а, б).
Рис. 9.6
Общая формула, по которой можно вычислить величину продольной силы N(zi) в произвольном поперечном сечении бруса (рис. 9.6, а, б), имеет вид
Ai
N( zi ) = ∑Fzi + ∑∫q z( zi )dzi , 0
где Fzi – внешние сосредоточенные силы; qz(zi) – интенсивность внешних распределенных сил, приложенных на рассматриваемом участке.
Суммирование производится по всем участкам, расположенным по одну сторону от рассматриваемого сечения.
Правило знаков. На брус действуют внешние силы Fi (рис. 9.7, а). N(z) считается положительной, если она вызывает деформацию растяжения отсеченной части, т. е. N(z1) направлено от сечения (рис. 9.7, б), и отрицательной, если она вызывает деформацию сжатия, т. е. N(z2) направлено к сечению (рис. 9.7, в).
190
9. Деформируемое твердое тело
Рис. 9.7
Величина продольного усилия N(zi) в i-м сечении численно равна алгебраической сумме проекций на ось z всех внешних сил, действующих на отсеченную часть бруса (Fz и q(z)), взятых со знаком «плюс», если они направлены от сечения, или – «минус», если направлены к сечению.
Пример 9.1. Для бруса (рис. 9.8) построить эпюру продольных сил, не учитывая влияния силы тяжести.
Рис. 9.8
Решение. Вычислять реакции опор в заделке нет смысла, так как при вычислении в любом сечении продольной силы N(zi) учитываем внешние силы со стороны свободного конца консоли.
Разделим брус на 3 участка (рис. 9.9, а) согласно заданному нагружению. Проведем произвольное поперечное сечение на каждом из участков и вычислим значения продольной силы Ni(zi).
I участок: 0 ≤ z1 ≤ a (рис. 9.9, б).
N1 (z1) = −F = −qa .
191
И. В. Богомаз. Механика
Продольная сила N1 постоянна на всем участке и вызывает сжатие всего I участка (N1(z1) < 0).
II участок: 0 ≤ z2 ≤ 2a (рис. 9.9, в).
|
N |
2 |
(0) = −F = −qa, |
N2 (z2 ) = qz2 |
|
|
|
− F → |
|
(2a) = +q 2a − F = +2qa −qa = qa. |
|
|
N |
2 |
|
|
|
|
Продольная сила N2 изменяется линейно на этом участке, при 0 ≤ z2 ≤ Fq участок сжат (N2(z2) < 0), при Fq ≤ z2 ≤ 2a участок растя-
нут (N2(z2) >0).
Рис. 9.9
192
9. Деформируемое твердое тело
III участок: 0 ≤ z3 ≤ 1,5a (рис. 9.9, г).
N3 (z3 ) = −2F + q 2a − F = −2qa + 2qa −qa = −qa .
Продольная сила N3 постоянна на всем участке и вызывает сжатие всего III участка (N3(z3) < 0). Значение реакции в заделке H соответствует значению продольной силы на III участке при z3 = 1,5a, т. е. H = N3 (z3 =1,5a) = qa и направлена к сечению.
Вычислив значения продольной силы N(z) на каждом участке, строим эпюру продольных сил. Для этого проведем параллельно оси бруса ось эпюры O – O (базис) и перпендикулярно к ней в выбранном масштабе отложим вычисленные значения N(zi) (рис. 9.9, д): положительные значения откладываем вверх, отрицательные − вниз. Соединяем полученные точки прямыми линиями и, проставив знаки в поле эпюры, заштриховываем линиями, перпендикулярными базисной линии.
Правила контроля построения эпюры N:
1.Эпюру рекомендуют проверять (читать) от свободного конца стержня, тогда можно четко проследить нагружение бруса.
2.В сечении, где приложена внешняя сила, на эпюре продольных сил N возникает скачок, высота которого равна величине этой силы.
3.На участках, не нагруженных распределенной нагрузкой, эпюра N ограничена прямыми, параллельными базисной линии.
4.На участке, где действует линейно-распределенная нагрузка q(z), усилие N изменяется по линейному закону и эпюра ограничена наклонной прямой.
Пример 9.2. Для ступенчатого бруса (рис. 9.10) построить эпюру продольных сил N, не учитывая влияние силы тяжести.
Решение. Разделим брус на три участка, согласно заданному нагружению и изменению площади поперечного сечения. Проводя поперечное сечение на каждом участке бруса, вычислим значения внутренних усилий N(zi) (рис. 9.11, а):
Рис. 9.10
193
И. В. Богомаз. Механика
I участок: 0 ≤ z1 ≤ 2a.
|
N (z = 0) = 3F =3qa, |
||
|
|
1 1 |
|
N (z1) = F −qz → |
N (z1 = 2a) = F −2 qa =3qa −2qa = qa. |
||
1 |
|
||
1 |
|||
|
|||
|
|
||
Продольная сила N(z1) является линейной функцией.
II участок: 0 ≤ z2 ≤ 2a.
N (z2 ) = F − 2 qa =qa (const).
Продольная сила N2 постоянна на всем участке.
III участок: 0 ≤ z3 ≤ 2,5a.
N (z3 ) = F − 2 qa + F − 2qz3 = 3qa − 2qa +3qa − 2qz3 = 4qa − 2qz3 .
Продольная сила N(z3) меняется по линейному закону.
|
|
N (z = 0) = 4qa, |
|
|
|
|
3 |
N (z ) = 4qa −2qz → |
= 2,5a) = 4qa −2q 2,5a = qa. |
||
3 |
3 |
N (z |
|
|
|
|
3 |
По вычисленным значениям строим эпюру N (рис. 9.11, б). Проверим эпюру, используя правила контроля.
Рис. 9.11
194
9. Деформируемое твердое тело
1.Размер и направление скачков на эпюре в сечениях бруса С
иD соответствует приложенным растягивающим внешним силам F = 3qa. Скачок в заделке должен соответствовать реакции. Проверим:
∑Fzi = 0, H −2q 2,5a + F − q 2a + F = 0,6;
H −5qa +3qa − 2qa +3qa = 0 → H = qa.
На участках I и III эпюра ограничена наклонной прямой, направление наклона соответствует направлению действия распределенной нагрузки q на соответствующих участках бруса.
На участке II продольная сила N постоянна, так как на этом участке брус свободен от нагружения распределенной нагрузкой.
Следует иметь в виду, что при переходе от одного участка к другому изменение площади сечения на величине продольной силы не сказывается.
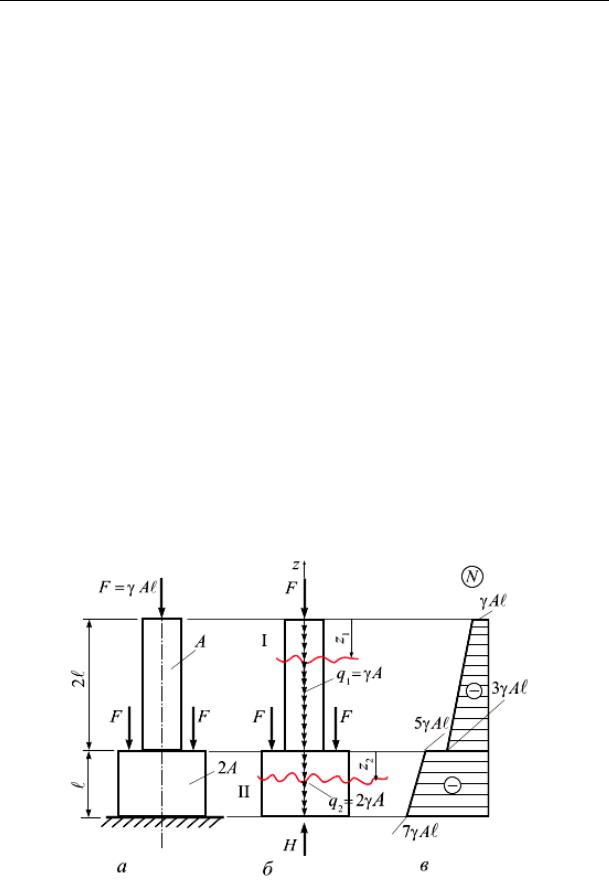
Пример 9.3. Для ступенчатого бруса (рис. 9.12, а) построить эпюру продольных сил с учетом действия собственного веса бруса при заданных условиях: удельный вес материала бруса γ, F = γАA.
Рис. 9.12
195
И. В. Богомаз. Механика
Решение. Собственный вес вертикального бруса можно рассматривать как продольную (осевую) внешнюю нагрузку, равномерно распределенную вдоль оси бруса, интенсивность которой
q = γАi ,
где Ai − площадь поперечного сечения i-го участка. Расчетная схема показана на рис. 9.12, б. Выделим на брусе два участка.
I участок: 0 ≤ z1 ≤ 2A.
Интенсивность распределенной нагрузки на этом участке q1 = γА;
N(z1 ) = −F −q1z1 = −γAA− γAz1 = −γA(A+ z1 ).
Продольная сила N(z1) вызывает сжатие I участка и является линейной функцией. Имеем
|
N (z = 0) = −γAA, |
|
|
|
1 |
N (z ) = −γA(A+ z1 )→ |
|
|
1 |
N (z = 2A) = −γA(A+ 2A)= −3γАA. |
|
|
|
1 |
II участок: 0 ≤ z2 ≤ A.
Интенсивность распределенной нагрузки на этом участке q2 = γ 2А= 2 q1;
N(z2 ) = F −q 2A−2F −q z2 = −γAA−γA 2A−2γAA−2γAz2 − =
= −γA(5A+ 2z2 ).
Продольная сила N(z2) вызывает сжатие II участка и является линейной функцией. Имеем
|
N (z = 0) = −5γAA, |
|
|
|
2 |
N (z ) = −γA(5A+ 2z2 )→ |
= A) = −γA(5A+ 2A)= −7γАA. |
|
2 |
N (z |
|
|
|
2 |
По вычисленным значениям строим эпюру N (рис. 9.12, в).
196
9. Деформируемое твердое тело
Проверим эпюру, используя правила контроля.
Cкачки на эпюре в двух сечениях бруса: при z1 = 0 на величину F = γАA и при z2 = 0 на величинуF = γАA, соответствуют величинам
этих сил, приложенным к брусу в этих сечениях. Скачок в заделке должен соответствовать реакции H. Проверим:
∑Fzi = 0, H −3F − q1 2A−q2 A = 0;
H −3γ AA− γ A 2A− 2γ A A = 0 → H = 7γ AA.
На участках I и II эпюра ограничена наклонной прямой Изменение N(z) на участках с действующей распределенной нагрузкой происходит по линейному закону.
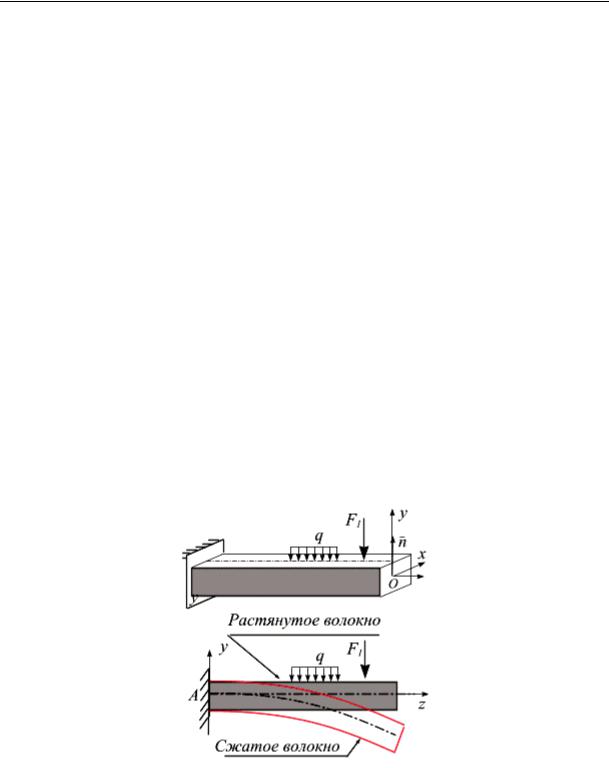
Построение эпюр продольной силы и изгибающего момента.
Если все нагрузки располагаются в одной плоскости, например, в плоскости Oyz, называемой силовой, то изгиб является плоским.
Деформацию плоского изгиба вызывают силы, лежащие в одной силовой плоскости Oyz (рис. 9.13). В любом поперечном сечении балки внутренние усилия приводятся, как правило, к поперечной силе Qy и изгибающему моменту Mx.
Рис. 9.13
Прямолинейный брус, работающий на изгиб, принято называть балкой.
Поперечная сила Qy(z) в сечении балки равна алгебраической сумме проекций всех внешних сил, действующих на балку по одну
197
И. В. Богомаз. Механика
сторону от рассматриваемого сечения, на нормаль к ее оси, проведенную в рассматриваемом поперечном сечении.
Qy (z) = ∑Fy (Fi )отс.ч. |
(9.2) |
Правило знаков для поперечной силы Qy. Рассмотрим балку АВ
(рис. 9.14, а). Поперечная сила Qy в сечении z считается положительной, если она направлена так, что стремится повернуть отсеченную часть по часовой стрелке (рис. 9.14, б).
Рис. 9.14
При построении эпюр поперечных сил положительные значения ординат откладывают вверх от оси эпюры, а отрицательные – вниз, полезно указывать знаки внутренних усилий.
Величина изгибающего момента Mx(z) в сечении балки равна алгебраической сумме моментов всех внешних сил, действующих на балку по одну сторону от рассматриваемого сечения относительно оси x, проходящей через центр тяжести рассматриваемого поперечного сечения балки перпендикулярно плоскости действия внешних сил.
M x (z) = ∑M x (Fi )отс.ч. |
(9.3) |
Правило знаков для изгибающего момента Mx. Рассмотрим балку АВ (рис. 9.15, а). Изгибающий момент считается положительным в сечении, если он направлен так, что вызывает растяжение нижних волокон бруса, и отрицательным, если растянуты верхние волокна бруса (рис. 9.15, б).
198
9. Деформируемое твердое тело
При расчете балок строительных конструкций эпюру изгибающих моментов принято строить со стороны растянутых волокон, т. е. положительные ординаты откладывают вниз от базисной линии, а отрицательные – вверх.
Отметим, что во избежание ошибки рекомендуется неизвестные внутренние усилия Qy и Mx принимать положительными.
Рис. 9.15
Рассмотрим балку АВ (рис. 9.16, а).
Рис. 9.16
Вычислим для сечения с координатой z внутренние Qy и Mx. Выделим левую отсеченную часть балки и в сечении покажем искомые внутренние усилия (рис. 9.16, б):
Qy = ∑Fy (Fi )отс.ч =VA − F ; M x = ∑Mc (Fi )отс.ч =VA z − F (z −a) .
199
И. В. Богомаз. Механика
Дифференциальные зависимости между q(z), Qy и Mx. Условим-
ся считать q(z) положительной, если ее направление совпадает с направлением оси ординат Oy. Между интенсивностью распределенной нагрузки q(z), поперечной силой Oy и изгибающим моментом Mx в сечении n – n при изгибе существуют дифференциальные зависимости
(рис. 9.17).
Рис. 9.17
Производная от поперечной силы по элементу длины балки равна интенсивности распределенной нагрузки:
dQy |
= q . |
(9.4) |
|
dz |
|||
|
|
Производная от изгибающего момента по элементу dz длины балки равна поперечной силе:
dM x |
= Qy . |
(9.5) |
|
||
dz |
|
|
Учитывая эти зависимости, можно сформулировать ряд положе-
ний.
1.Участкам с восходящими (слева направо) ординатами эпюры
Mx соответствуют участки с отрицательными значениями Oy, а участки с нисходящими ординатами эпюры Mx – участки с положительными значениями Oy.
2.В сечениях, где Oy = 0, изгибающий момент максимальный или минимальный.
200
9. Деформируемое твердое тело
3.Между сосредоточенными силами (если между ними отсутст-
вует распределенная сила) эпюра Mx ограничена прямой (в общем случае наклонной), эпюра Oy – прямой горизонтальной линией.
4.На участках с распределенной нагрузкой эпюра Mx ограничена параболой второй степени, а эпюра Oy – наклонной прямой.
5.Точкам приложения сосредоточенных сил, перпендикулярных
оси балки, соответствуют переломы в эпюре Mx и скачки в эпюре Oy. Когда сила направлена вниз, то и скачок в эпюре Oy при перемещении слева направо должен быть направлен вниз; когда сила направлена вверх, то и скачок должен быть вверх. Величина скачка равна величине силы.
6.В сечении, где приложен сосредоточенный момент, на эпюре Mx скачки, равные величине этого момента.
Пример 9.4. Для балки (рис. 9.18, а) построить эпюры Mx и Qy. Длина пролетов балки A1 = 4м; A2 = 5 м, приложенная сила F = 10 кН.
Рис. 9.18
Решение. Отбросим опоры А и В, заменим их действие реакциями. Направим реакции опор вертикально вверх, запишем уравнения равновесия для полученной системы параллельных сил и вычислим реакции опор (рис. 9.18, б):
201
И. В. Богомаз. Механика
∑M A = 0, RB (A1 +A2 ) − F A1 = 0 →
RB = F |
|
A1 |
=10 |
|
4 |
= 4, 44 |
кН. |
|||
(A1 |
+ A2 ) |
(4 |
+5) |
|||||||
|
|
|
|
|
|
|||||
∑M B = 0, RA (A1 +A2 ) − F A2 = 0 → |
||||||||||
RA = F |
|
A2 |
|
=10 |
|
5 |
|
= 5,56 |
кН. |
|
(A1 |
+ A2 ) |
|
(4 |
+5) |
|
|||||
|
|
|
|
|
|
|||||
Проверка: ∑Fy = RA + RB − F = 5,56 + 4,44 = 0.
Проставляем значения реакций на схеме.
Разобьем балку на два участка. Составим выражения Mx и Qy по участкам и вычислим их значения в характерных сечениях.
I участок: 0 ≤ z1 ≤ A1 = 4 м.
Qy (z1) = RА = 5,56 кН.
Поперечная сила на этом участке является постоянной величиной.
|
|
|
|
M |
x |
(z |
= 0) = 0, |
|
M |
|
(z ) = R |
z |
|
1 |
|
|
|
x |
→ |
|
(z |
= 4) = R |
4 =5,56 4 = 22, 24кН м. |
|||
|
1 |
A 1 |
M |
x |
||||
|
|
|
|
|
1 |
|
A |
II участок: 0 ≤ z2 ≤ 4 м.
Qy (z2 ) = −RВ = −4,44 кН.
Поперечная сила на этом участке является постоянной величиной.
M x (z2 ) = RB z1 |
Mx (z2 |
= 0) |
= 0, |
|
||||
→ |
M |
|
(z |
|
=5) |
= R |
5 = 4,44 5 = 22, 24кН м. |
|
|
|
x |
2 |
|||||
|
|
|
|
B |
|
|||
Отложим полученные |
значения |
на эпюре Mx и эпюре Qy |
||||||
(рис. 9.18, в, г).
202
9. Деформируемое твердое тело
На эпюре Qy скачки: в сечении А скачок на величину RA; в сечении В скачок на величину RB; в сечении, где приложена сила F, скачок на величину этой силы F.
При обходе эпюр Mx и Qy слева направо замечаем: на участке I Mx возрастает, Qy положительная; участке II Mx убывает, Qy отрицательная.
Пример 9.5. Для шарнирно-опертой балки построить эпюры Qy и Mx (рис. 9.19, а). Дано: длина пролета балки A = 6 м; m1 = 24 кН · м,
m2 = 12 кН · м.
Рис. 9.19
Решение. Отбросим опоры А и В, заменим их действие реакциями. Направим реакции опор вертикально вверх, запишем уравнения равновесия для полученной системы параллельных сил и вычислим реакции опор (рис. 9.19, б):
∑M A = 0, RB A+ m2 −m1 = 0 →
RB = 1A(−m2 + m1) = 16 (−12 + 24) = 2 кН;
203
И. В. Богомаз. Механика
∑M B = 0, RA A−m1 + m2 − = 0 →
RA = 1A(−m2 + m1) = 14 (−12 + 20) = 2 кН.
Проверка: ∑Fy = −RA + RB = −2 + 2 = 0.
Разбиваем балку на три участка.
I участок: 0 ≤ z |
|
≤ 1 A = 1 |
6 = 2 м. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
1 |
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Qy (z1) = RА = |
|
|
|
|
−2 |
|
|
|
|
кН, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x (z1) = RА |
z1 |
M x (z1 = 0) = 0, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4 |
|
кН м. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
M x (z1 = 2) = −RА 2 = −2 2 = |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II участок: 0 ≤ z2 ≤ 2 A = 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qy (z2 ) = RA = |
|
|
−2 |
|
|
кН, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
M x (z2 ) = RA (2 + z2 ) −m1 → |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
M |
|
(z |
= |
0) = R |
|
|
2 |
−m |
= 2 2 −24 = |
|
−20 |
|
кН м, |
||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
x |
2 |
|
|
|
A |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
(z2 |
= 2) = RA 4 |
−m1 = 2 4 −24 = |
|
−16 |
|
кН м. |
|
||||||||||||||||||||||||||||
M x |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III участок: 0 ≤ z3 ≤ 1 A = 2 м. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qy (z3 ) = RB = |
|
−2 |
|
кН, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
M x (z3 ) = RB |
z3 → |
M |
x |
(z = 0) = 0, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
M |
3 |
= 2) = R 2 = 2 |
2 |
|
= 4кН |
м. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
(z |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|||||||
Эпюры Mx и Qy представлены на рис. 9.19, в, г.
204
9. Деформируемое твердое тело
В сечениях, где приложены пары m1 и m2, на эпюре Mx скачки, равные величинам моментов этих пар.
Пример 9.6. Балка АВ (рис. 9.20, а) загружена распределенной нагрузкой интенсивностью q. Построить эпюры изгибающего момента Mx и поперечной силы Qy. Длина пролета балки A = 8 м, интенсивность распределенной нагрузки q = 4 Н/м.
Решение. Отбросим опоры А и В, заменим их действие реакциями. Направим реакции опор вертикально вверх, запишем уравнения равновесия для полученной системы параллельных сил и вычислим реакции опор (рис. 9.20, б):
∑M A = 0 , RB 2A + 4A −q 4A 8A + 2A = 0,
RB (4 + 2)−4 2(1+ 4)= 0 → RB = 16 40 = 203 ≈ 6,7 кН;
∑M B = 0 , −RA 2A + 4A + q 4A 8A = 0 ,
−RA (4 + 2)+ 4 2 1 = 0 → RA = 16 8 = 43 ≈1,3 кН;
Проверка: ∑Fy = RA −q |
A |
+ RB = 6,7 −8 +1,3 = 0 . |
||||||||||
|
||||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
Разбиваем балку на два участка. |
|
|
|
|
|
|||||||
I участок: 0 ≤ z1 ≤ A/ 2 = 4м. |
|
|
|
|
|
|||||||
|
Qy (z1) = RА =1,3 кН, |
|
||||||||||
|
|
|
(z1 = 0) = 0, |
|
|
|
|
|
||||
M x (z1) = RА z1 |
M x |
|
|
|
|
. |
||||||
→ |
|
|
|
|
A |
|
|
|
A |
=1,3 8 |
||
|
M |
x |
(z = |
) = R |
А |
|
= 5, 2 кН м. |
|||||
|
|
|
||||||||||
|
|
1 |
2 |
|
2 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|||||
205
И. В. Богомаз. Механика
Рис. 9.20
II участок: (0 ≤ z2 ≤ A/ 4 = 2). |
|
|
|
|
||||||||
|
|
|
|
|
|
= 0) = −RB = −6,7 кН, |
||||||
Qy (z2 ) = −RB + q z2 |
→ |
Qy (z2 |
||||||||||
|
|
|
|
|
A |
|
|
|
A |
|
||
|
|
Q |
(z |
2 |
= |
) = −R |
+ q |
= −6,7 + 4 2 =1,3кН. |
||||
|
|
|
|
|||||||||
|
|
|
y |
|
4 |
|
B |
4 |
|
|||
|
|
|
|
|
|
|
|
|
||||
Поперечная сила на II участке меняет знак «плюс» на знак «минус». В этом случае изгибающий момент Mx достигает экстремального значения. Вычислим значение z2 = z0, при котором поперечная сила Qy(z0) = 0, а изгибающий момент достигает экстремума:
Qy (z0 ) = −RB + q z0 = 0 → z0 = RqB = 6,47 =1,67 кН.
206
|
|
|
|
|
|
|
|
|
|
|
9. |
Деформируемое твердое тело |
||||
|
|
M |
|
(z |
|
) = R z |
|
− qz |
|
|
z2 |
|
= |
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x |
|
2 |
B |
2 |
|
2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x (z2 |
= 0) = 0, |
|
|
|
|
|
|
|
|
|
||||
|
z2 |
|
|
|
|
|
|
|
|
|
22 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= 6,7z2 −4 |
2 |
→ M x (z2 |
= 2) = 6,7 2 − |
4 |
|
|
= 5,2кH м, |
|||||||||
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
=1,67) = 6,7 1,67 −41,67 |
2 |
|||||||||
|
|
M x (zo |
= 5,61кH м. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Эпюры Mx и Qy представлены на рис. 9.20, в, г.
Пример 9.7. Построить эпюры поперечных сил и изгибающих моментов для консольной балки, нагруженной, как показано на рис. 9.21, если F = 20 кН; q = 10 кН/м; M = 20 кН м.
Рис. 9.21
Решение. Отбросим опоры А и В, заменим их действие реакциями. Направим реакции опор вертикально вверх, запишем уравнения равновесия для полученной системы параллельных сил и вычислим реакции опор (рис. 9.22, а):
∑M А =0 , −q 6 3 −m + RB 10 − F 14 = 0 →
R |
= q 6 3 + m + F 14 |
= |
10 18 + 20 + 20 14 |
= 48 (кН); |
|
||||
B |
10 |
10 |
|
|
|
|
|||
∑MB =0 , −RА 10 + q 6 7 −m − F 14 = 0 →
207
И. В. Богомаз. Механика
RА = q 6 7 −m − F 14 |
= |
10 42 −20 −20 14 |
=32 |
(кН). |
10 |
|
10 |
|
|
Проверка: ∑Fy = RА −q 6 + RB − F =32 −10 6 + 48 −20 = 0.
Для построения эпюр Qy и Mx разделим балку на 4 участка и покажем начало и направление отсчета на каждом участке координатой zi. Составим выражения Qy(zi) и Mx(zi) на каждом участке, мысленно представляя отсеченную часть под действием внешней нагрузки, используя выражения и правило знаков, выведенные ранее:
Qy (zi ) = ∑y (Fi )отс.ч , M x (zi ) = ∑mс(Fi )отс.ч .
|
|
|
|
|
|
Рис. 9.22 |
|
|
I участок: 0 ≤ z1 ≤ 2 м. |
|
|
|
|||||
|
|
|
|
|
Q |
(z = 0) = R |
А |
= 32кН, |
Q |
|
(z ) = R |
|
−q z |
y |
1 |
|
|
y |
А |
→ |
(z1 = 2) = RА −q 2 = 32 −10 2 =12кН. |
|||||
|
1 |
1 |
Qy |
|||||
|
|
|
|
|
|
|
|
|
208
9. Деформируемое твердое тело
|
z |
2 |
M |
x |
(z |
= 0) = 0, |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
4 |
|
|
|||
M x (z1) =VАz1 −q |
1 |
→ |
|
(z1 |
= 2) = RА2 −q |
|
= 32 2 |
−10 |
= 44кН м. |
|||||
|
|
|
||||||||||||
|
2 |
M x |
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
На этом участке растянуто нижнее волокно.
II участок: 0 ≤ z2 ≤ 4 м.
Qy (z2 ) = RА −q (2 + z |
Qy (z2 = 0) |
= RА = 32кН, |
||||
|
|
|
= RА −q (2 + 4)= 32 −10 6 = |
|||
2 )→ Qy (z2 |
= 4) |
|||||
|
|
|
−28 |
|
кН. |
|
|
= |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Поперечная сила на II участке меняет знак «плюс» на знак «минус». В этом случае изгибающий момент Mx достигает экстремального значения. Вычислим значение z2 = z0, при котором поперечная сила Qy(z0) = 0, а изгибающий момент достигает экстремума:
|
|
Qy (z2 = z0 ) = RА −q (2 + z0 ) |
= 0 → z = 32 −2 10 |
=1,2 м. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
10 |
|
|
||
|
|
|
|
|
M x (z2 ) = RА (2 + z2 )+ m |
− |
q(2 + z2 )2 |
→ |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q(2) |
2 |
|
|
|
|
|
|
|
|
|
|
M |
x |
(z |
2 |
= 0) = R |
А |
|
2 + m − |
|
|
|
= 32 2 + 20 −10 2 = 64кН м, |
||||||||||
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z2 |
= 4) = 6RА |
+ m − q(2 + 4) |
2 |
|
|
|
−10 6 |
2 |
|
|||||||||
M x |
|
= 32 6 + 20 |
|
= 32кН м. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
Экстремальное значение момента при z0 = 1,2 м |
|
|
||||||||||||||||||
|
|
|
|
|
M (z |
2 |
= z ) = R (2 +1,2) + m − |
q( |
2 +1,2)2 |
= |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
max |
|
o |
A |
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
= 32 3, 2 + 20 −10 |
3, 22 |
= 71, 2 кН м. |
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
209
9. Деформируемое твердое тело
Построение эпюр N, Qy и Mx для плоских рам. Рамой называют систему из прямолинейных стержней, расположенных в одной плоскости и соединенных между собой жесткими узлами. Ось рамы представляет собой ломаную линию. Рама называется плоской, если ось рамы и приложенная внешняя нагрузка лежат в одной плоскости.
При построении эпюр пользуются теоремой о параллельном переносе силы из раздела «Статика» теоретической механики:
Сила F , приложенная в произвольной точке тела A, эквивалентна силе, перенесенной в другую точку B параллельно самой себе и присоединенной паре, момент которой MB = F · AB.
Момент MB называется присоединенной парой.
С выбранным участком рамы совмещают систему координат Oyz. При этом ось Oz всегда направляют по оси рассматриваемого стержня, ось Oy размещают в плоскости сечения стержня.
В общем случае в поперечных сечениях стержней плоской рамы возникают три внутренних силовых фактора: продольная сила N(z), поперечная сила Qy(z) и изгибающий момент Mx(z).
При построении эпюр Nz, Qy и Mx пользуются методом сечений. Рама мысленно делится на отдельные прямолинейные стержни, для каждого из которых эпюры внутренних силовых факторов строятся по тем же правилам, что и для бруса. В выбранном сечении мысленно выделяют сечение zi.
Чтобы получить выражение продольной силы N(z), нужно спроецировать силы, приложенные к части рамы, лежащей по одну сторону
от этого сечения, на ось стержня – N(zi ) = ∑Fi z ; для поперечной силы
Qy(z) нужно спроецировать внешние силы на ось, нормальную оси стержня, – Qy (zi ) = ∑Fiy . Сохраняется принятое ранее правило знаков.
Положительные ординаты N(z) и Qy(z) откладывают с внешней стороны рамы, отрицательные − с внутренней (если конфигурация рамы такова, что можно различить ее наружную или внутреннюю стороны).
Для изгибающего момента M x (z) = ∑Fiy zi специального пра-
вила знаков не устанавливают, при составлении функции Mx(z) принимают по собственному усмотрению какой-либо момент положи-
211
9. Деформируемое твердое тело
Участок ВС: 0 ≤ z2 ≤ 2a (рис. 9.24, в).
Силу F с участка СD перенесем параллельно самой себе в точку С, при этом учитываем присоединенную пару MC = F · a.
Тогда
N2 = F = qa;
|
|
|
|
|
Q2 (z2 ) =q z2 → |
Q (z |
|
= 0) = 0, |
|
|
|
|
|
|||||||||
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Q2 (z2 = 2a) = 2 qа; |
|
|
|
||||||||
|
|
|
|
|
|
qz |
2 |
|
|
M |
x |
(z |
2 |
= 0) = 0, |
|
|
|
2 |
|
|
||
M |
|
(z |
|
) = qa2 |
|
2 |
М |
|
|
|
|
|
|
|
|
q (2a) |
|
|
||||
|
|
− |
|
|
→ |
|
|
|
|
2a) = qа |
2 |
− |
= −qа |
2 |
. |
|||||||
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
x |
|
2 |
|
|
|
2 |
M x (z2 = |
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.24
213
9. Деформируемое твердое тело
Рис. 9.25
3.Проверим равновесие узла рамы. Проведем сечение n – n
ивыделим узел В (рис. 9.25, д). К выделенному узлу приложим внеш-
нюю нагрузку, а в местах сечений − продольные, поперечные силы и изгибающие моменты в соответствии с эпюрами Nz, Qy и Mx. Составим уравнения равновесия для отсеченной части:
∑Fx = −qа+qа = 0, ∑Fy = 2qа−2qа=0 .
Рама находится в равновесии.
215
9. Деформируемое твердое тело
Разделим раму на пять участков (рис. 9.27, а) и выберем направление осей Oxz. На каждом участке в произвольном месте проведем сечение и запишем выражения для внутренних усилий.
Участок АС: 0 ≤ z1 ≤ 3a (рис. 9.27, б).
Рассмотрим равновесие в сечении z1. Продольная сила
N1(z1)= RA = qa.
Поперечная сила |
|
Q1( z1 ) = −q z1 |
Q ( z = 0 ) = 0, |
→ 1 1 |
|
|
Q1( z1 = 3а) = −3qа. |
Изгибающий момент |
|
|
qz |
2 |
|
|
(z1 |
= |
0) |
= |
0, |
M1x (z1) = |
1 |
М1 |
|
|
|||||
→ |
|
|
|
|
|
|
|||
|
|
(z |
=3a) = 4,5qа2. |
||||||
|
2 |
|
М |
||||||
|
|
|
|
1 |
1 |
|
|
|
|
На этом участке растянуто наружное волокно стержня АС.
Участок СЕ: 0 ≤ z2 ≤ a.
Рассмотрим равновесие левой части рамы (рис. 9.27, в). Силу Q = q · 3a перенесем параллельно самой себе в точку С, при этом добавляем присоединенную пару, момент MC(Q) которой равен
MC (Q) =Q 1,5а = q 3a 1,5а = 4,5qa2 .
Тогда продольная сила N2(z2)= Q = –3qa. Поперечная сила Qy(z2)= –RA = –qa. Изгибающий момент
|
|
Мx (z2 |
= 0) = 4,5qа2 , |
M2x (z2 ) = MC (Q) + RA z2 |
= 4,5 qа2 + qа z |
|
= a) = |
→ Мx (z2 |
|||
|
2 |
|
|
|
|
= 4,5qа2 + qа2 = 5,5qа.2 |
|
На этом участке растянуто наружное волокно.
217
9. Деформируемое твердое тело
Изгибающий момент
|
|
|
|
(z3 |
= 0) = 0, |
M3x (z3 ) = HB z3 |
= 2qa z3 |
Мx |
|||
→ |
|
(z |
=1,5a) =3qа2. |
||
|
|
М |
x |
||
|
|
|
3 |
|
|
На этом участке растянуто наружное волокно.
Участок KD: 0 ≤ z4 ≤ 1,5a (рис. 9.27, д).
Продольная сила
N4(z4)= –VB = –qa.
Поперечная сила
Q4(z4)= HB + F = 2qa + qa = 3qa.
Изгибающий момент
M4x (z4 ) = HB (1,5а+ z4 ) + F z4 = 2qa(1,5а+ z4 ) + qa z4 .
Имеем |
|
|
|
|
|
|
|
|
|
|
|
М |
x |
(z |
= 0) = 3qа2 |
, |
|
|
|||
|
|
3 |
|
|
|
|
|
|
||
M4x (z4 ) = 2qa(1,5а+ z4 ) +qa z4 |
Мx (z4 |
=1,5a) = |
|
|
|
|
||||
→ |
|
|
|
|
|
|
+qa 1,5a = |
|||
|
= 2qa(1,5а+1,5a) |
|||||||||
|
|
|
|
2 |
+1,5qа |
2 |
= |
7,5qа |
2 |
. |
|
= 6qа |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
На этом участке растянуто наружное волокно.
Участок ЕD: 0 ≤ z5 ≤ a (рис. 9.27, е).
Силы HB = 2qa и F = qa перенесем параллельно самим себе в точку D, при этом добавляем присоединенные пары с моментами
M D (HB ) = H B 3а = 2qa 3а = 6qa2 ;
M D (F ) = F 1,5а = qa 1,5а =1,5qa2 .
Тогда продольная сила
N5(z5)= –HB – F = –2qa – qa = –32qa.
219
9. Деформируемое твердое тело
∑MD =VA 2а+q 3a 1,5a +m − F 1,5a − HB 3a =
=2qa2 +4,5qa2 +qa2 −1,5qa2 −6qa2 = 0.
Рис. 9.28
Следовательно, выделенный узел рамы находится в равновесии.
221