15. Устойчивость сжатых стержней

15. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

15.1. Понятие об устойчивости

В предыдущих главах мы определяли поперечные размеры стержней из условий прочности. Однако разрушение стержня может произойти не только потому, что будет нарушена прочность, но и оттого, что стержень не сохранит той формы, которая ему придана конструктором; при этом изменится и характер напряженного состояния в стержне. При проектировании конструкций наряду с анализом прочности и жесткости проводится анализ их устойчивости.

Наиболее типичным примером является работа стержня, сжатого силами F. В поперечном сечении, перпендикулярном к оси стержня, внутренние усилия в любом сечении zi приводятся только к продольной силе N(zi), при этом в любой точке поперечного сечения бруса возникает нормальноенапряжение, котороенедолжнопревышатьдопустимого:

	σ =	N(zi )	≤[σ],	(15.1)
		A

где A − площадь поперечного сечения.

Это условие предполагает, что стержень все время вплоть до разрушения работает на осевое сжатие. Уже простейший опыт показывает, что далеко не всегда возможно разрушить стержень путем доведения напряжений сжатия до предела текучести или предела прочности материала.

Если мы подвергнем продольному сжатию тонкую деревянную или пластмассовую линейку, то она может сломаться, изогнувшись перед изломом. Сжимающие силы, при которых произойдет разрушение линейки, будут значительно меньше тех, которые вызвали бы при простом сжатии напряжение, равное пределу прочности материала. Разрушение линейки произойдет потому, что она не сможет сохранить приданную ей форму прямолинейного сжатого стержня, а искривится, что вызовет появление изгибающих моментов от сжимающих сил F и, стало быть, добавочные напряжения от изгиба; линейка потеряет устойчивость.

Устойчивость конструкции − способность конструкции сохранять под нагрузкой начальную форму упругого равновесия.

317

И. В. Богомаз. Механика

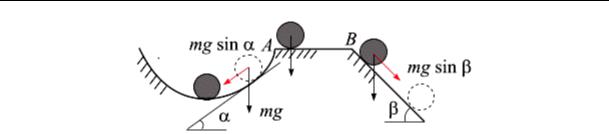
Рис. 15.1

Явление потери устойчивости при сжатии можно по аналогии иллюстрировать следующим примером из механики абсолютно твердого тела (рис. 15.1). Рассмотрим движение цилиндра по трем гладким поверхностям. После малого отклонения цилиндра от исходного положения из ямки цилиндр возвращается в исходное положение проекцией mg · sinα – в состояние устойчивого равновесия. На горизонтальной площадке AB равновесие цилиндра делается безразличным. Если цилиндр отклонить, он остается в равновесии и в новом положении, которое также является устойчивым. Как только цилиндр окажется в точке B, его равновесие сделается неустойчивым. При малейшем толчке вправо цилиндр начнет двигаться вниз по наклонной поверхности под действием силы mg · sinβ.

Рассмотренный пример об устойчивости занимаемого положения цилиндра не зависит от величины действующей на цилиндр силы.

В механике деформируемого твердого тела вид равновесия зависит от величины приложенной к телу сил (нагрузки). При этом ре-

шается задача об устойчивости формы упругого равновесия.

Потерю устойчивости прямого сжатого стержня иногда называют «продольным изгибом», так как она влечет за собой значительное искривление стержня под действием продольных сил. Определим, при каком значении осевой сжимающей силы F такое искривление возможно.

Эту задачу в 1744 г. впервые решил академик Петербургской Академии наук Л. Эйлер.

15.2. Продольный изгиб. Потеря устойчивости

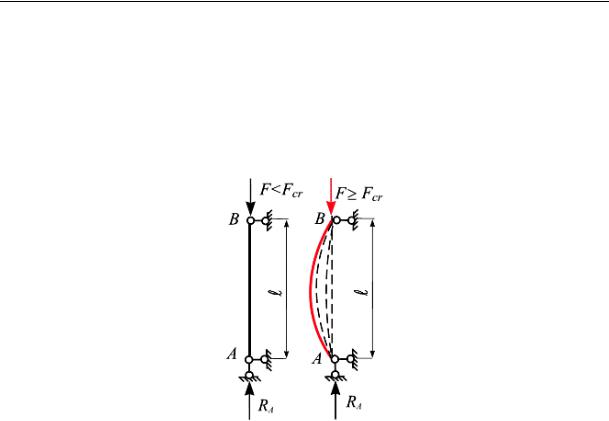
Рассмотрим достаточно длинный по сравнению с его поперечными размерами стержень, шарнирно опертый по концам; опора В допускает возможность продольного перемещения верхнего конца стержня (рис. 15. 2). Нагрузим его сверху центрально силой F, посте-

318

15. Устойчивость сжатых стержней

пенно возрастающей. Мы увидим, что пока сила F сравнительно мала, стержень будет сохранять прямолинейную форму.

При попытках отклонить его в сторону, например путем приложения кратковременно действующей горизонтальной силы, он будет после ряда колебаний возвращаться к первоначальной прямолинейной форме, как только будет удалена добавочная сила, вызвавшая отклонение.

Рис. 15.2

При постепенном увеличении силы F стержень будет все медленнее возвращаться к первоначальному положению, увеличивая силу F до такой величины, при которой стержень после небольшого отклонения его в сторону уже не выпрямится, а останется искривленным. Если мы, не удаляя силы F, выпрямим стержень, он уже, как правило, не сможет сохранить прямолинейную форму. Другими словами, при этом значении силы F, называемой критической силой, будем иметь такое состояние равновесия, когда исключается вероятность сохранения стержнем заданной ему прямолинейной формы.

Наименьшее значение осевой сжимающей силы, при которой прямолинейная форма равновесия перестает быть устойчивой и заменяется другой (искривленной) формой равновесия, называется критической силой Fcr.

Приложение к стержню продольной силы, даже незначительно превышающей Fcr, приводит к потере устойчивости первоначальной прямолинейной формы равновесия, а стержень изгибается. Это явление называется продольным изгибом. Появление продольного изгиба опасно тем, что происходит очень быстрое нарастание прогиба, и стержень теряет устойчивость. Это приводит, как правило,

319

И. В. Богомаз. Механика

к разрушению конструкции либо к появлению недопустимых пластических деформаций, что делает стержень непригодным к работе.

В курсе сопротивления материалов рассматривается задача об устойчивости прямолинейных сжатых стержней. Более сложные случаи рассматриваются в специальном курсе «Устойчивость и динамика сооружений».

Для обеспечения безопасности сооружения помимо проверки на прочность по формуле (15.1) необходима и проверка на условие устойчивости:

F ≤	Fcr	,	(15.2)
	K

где F – рабочая нагрузка; Fcr – критическая нагрузка; K – коэффициент запаса по устойчивости, который зависит от назначения стержня и его материала; для стальных стержней принимают K =1,5 ÷3 ; для чугунных – K = 5; для деревянных – K = 3.

Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей нагрузке при расчете на прочность. Важно подчеркнуть, что потеря устойчивости может произойти при напряжениях, значительно меньших тех, которые допустимы с точки зрения прочности конструкции.

15.3. Формула Эйлера для вычисления критической силы шарнирно закрепленного стержня

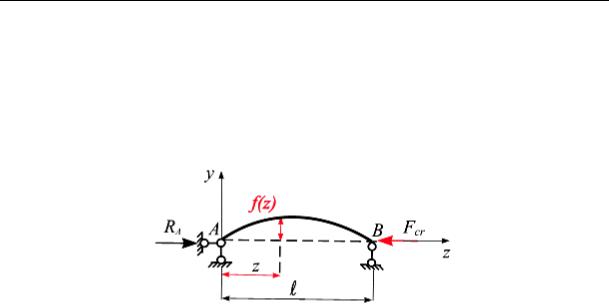
Постановка задачи. Вычислить критическую силу для центрально сжатого стержня, шарнирно опертого по концам (рис. 15.3), при которой возможно равновесие стержня с изогнутой осью. Л. Эйлер рассмотрел эту задачу при малых деформациях и при условии, что в стержне отсутствуют начальные несовершенства, т. е. его ось – прямая линия, а материал однородный.

Предположим, что напряжения изгиба в результате действия Fcr не превышают предела пропорциональности σpr, т. е. материал деформируется в зоне упругости (справедлив закон Гука.). При малых прогибах справедливо приближенное уравнение упругой линии, фор-

мула (13.14)

320

15. Устойчивость сжатых стержней

	K =	1	≈	d2 f (z)	=	M	x	(z)	,	(15.3)
		ρ		d z2		E Jx

где f(z) – отклонение оси стержня от горизонтального положения – прогиб.

Рис. 15.3

Абсолютное значение изгибающего момента в произвольном сечении стержня M x = F f (z), тогда дифференциальное уравнение упругой линии стержня (15.3) будет иметь вид

d2v(z)	= −	F f (z)	→ f ′′+	F	f = 0.	(15.4)
d z2		EJx		EJx

Знак «минус» поставлен потому, что независимо от выбора по-

ложительного направления оси у знаки кривизны ρ1 и прогиба f(z) бу-

дут противоположны. Введем обозначение

	F	= k 2 .	(15.5)
	E Jx
Тогда уравнение (15.4) будет иметь вид
f ''+ k 2 f = 0.			(15.6)

Решение дифференциального уравнения (15.6) имеет вид

f (z) =C sin kz+D cos kz .

(15.7)

321

И. В. Богомаз. Механика

Произвольные постоянные C и D определяются из граничных условий задачи:

fA (z = 0) = 0; fB (z = ) = 0.

Имеем

fA (z = 0) =C sin 0+D cos 0 =0 → D 1 = 0 → D = 0.

Запишем решение дифференциального уравнения (15.7) в виде:

		f (z) =Csin kz.	(15.8)
	Имеем	C = 0;
	fB (z =
		) = C sin k = 0 →	= 0.
		sink

Из этого равенства следует, что, если C = 0, прогибы f(z) во всех сечениях стержня равны нулю, то это противоречит исходному пред-

положению задачи. Из второго условия sin k = 0, получим
k = nπ → k = n π, n =1, 2, 3, ...	(15.9)

Тогда из (15.5) с учетом (15.9) получим формулу для сжимающей силы:

	F	= k2	n π 2			π2 EJ	x n2 ,
			=		→ F =	2		n =1, 2, 3, ... (15.10)
	EJx

Как видно из (15.10), сжимающая сила F имеет множество значений. Для инженерных расчетов практический интерес представляет наименьшее значение этой силы. Полагая n =1 и имея в виду, что продольный изгиб произойдет в плоскости наименьшей жесткости, получим формулу для вычисления критической силы

	F =	π2 EJ	min .	(15.11)
		2
	cr

322

15. Устойчивость сжатых стержней

Формула (15.11) называется формулой Эйлера.

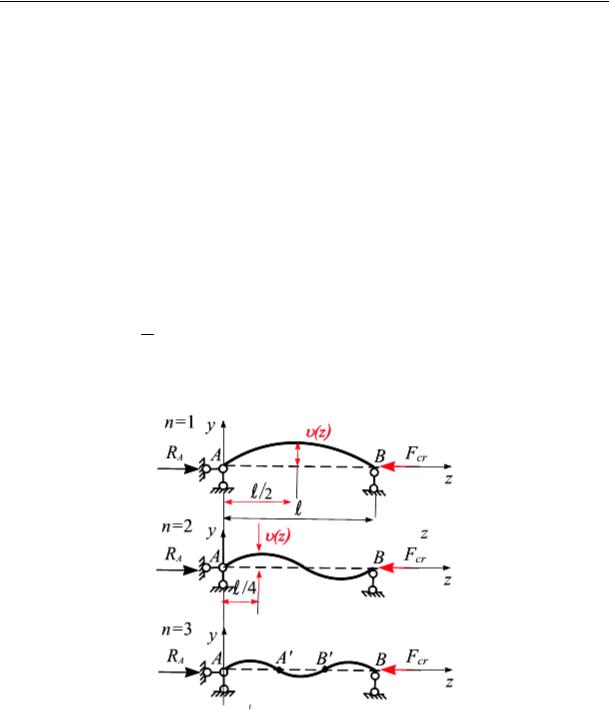
Анализ формулы Эйлера. Значениям критической силы высших порядков соответствуют искривления по синусоидам с двумя, тремя и т. д. полуволнами (рис. 15.4):

						2π									3π
f (z) = C sin								4,	f (z) = Csin								,
			1
		=	2		,						=	1		,			(15.12)
n = 2 T									n = 3 T
				4π2 E Jx								3
F =									F =				9π2 E Jx			.
					2
	cr									cr				2

Здесь T = n – период волны.

Рис. 15.4

Более полные исследования показывают, что формы равновесия, определяемые формулами (15.12), неустойчивы; они переходят в устойчивые формы лишь при наличии промежуточных опор в точках A′

и B′ (рис. 15.4).

Таким образом, чем больше точек перегиба будет иметь сину- соидально-искривленная ось стержня, тем большей должна быть кри-

323

И. В. Богомаз. Механика

тическая сила. Амплитуда синусоиды fmax (наибольший прогиб) неопределенна, так как при значении силы Fcr равновесие изогнутого стержня возможно при различных отклонениях его от прямолинейной формы, лишь бы эти отклонения были малыми.

15.4. Влияние способов закрепления концов стержня на величину критическойсилы

Формула Эйлера (15.11) получена для стержня, шарнирно опертого по концам. Задача с другими граничными условиями может иметь другие решения. Результаты анализа различных закреплений показывают, что во всех случаях критическую силу можно вычислять по обобщенной формуле

F =	π2 EJ	x	,	(15.13)
cr	(μ )2

где μ – коэффициент приведения, зависящий от способа закрепления концов стержня; – фактическая длина; 0 =μ 0 – приведенная

длина стержня.

Приведенная длина стержня 0 представляет собой длину полу-

волны между точками перегиба В и В’ изогнутой оси стержня, в которых изгибающие моменты равны нулю.

Во всех случаях значение коэффициента приведения μ определяется путем простого сопоставления изогнутого стержня с длиной полуволны синусоиды при шарнирном закреплении (рис. 15.5, а).

Консольный стержень длиной (рис. 15.5, б) можно рассматривать как половину воображаемого шарнирно опертого по концам стержня длиной 0 = 2 , т. е. μ = 2.

Для стержня (рис. 15.5, в) длина полуволны составляет 0 = 0,7 ,

т. е. μ = 0,7.

Для стержня с двумя защемлениями (рис. 15.6, г) длина полуволны между точками перегиба составляет половину длины стержня, т. е. 0 = 0,5 , и μ = 0,5. Заметим, что верхний конец стержня защем-

лен по отношению к изгибным деформациям, но свободно смещается в вертикальном направлении (скользит по направляющим).

324