И. В. Богомаз. Механика

10. ПОНЯТИЕ О НАПРЯЖЕНИИ И ДЕФОРМАЦИИ

10.1. Напряженное состояние в точке

Внутри вещества имеют место взаимодействия между частицами. Общие свойства этих взаимодействий обнаруживаются, если рассмотреть, как можно приложить внешние силы к твердому телу, имеющему одну закрепленную грань. Они могут быть приложены к любой части поверхности, и тело можно сжимать либо растягивать перпендикулярно этой поверхности. Можно приложить касательное силовое воздействие подобно трению.

Понятие напряженного состояния обобщает представление о силе, действующей через поверхность на все элементы поверхности и внутренние элементы тела. Если dA – малый элемент поверхности, нормаль которого имеет направление n , то говорят о взаимодействии через dA сил, действующих между частицами, находящимися на противоположных сторонах этого элемента поверхности. Компоненты силы зависят как от величины силы, так и от направления dA.

Рассмотрим отсеченную часть бруса (рис. 10.1). В окрестности точки К выделим элементарную площадку A, нормаль которой имеет направление n и в пределах которой равнодействующая внутрен-

	них сил равна			. Отношение		R		= p	представляет собой среднее
			R
					A			m

напряжение на площадке A.

Рис. 10.1

222

10. Понятие о напряжении и деформации

Получим полное напряжение p в точке K.

					Сила
p = lim		R
						.	(10.1)
A→0	A				Площадь

В системе СИ напряжение выражается в паскалях Па = Н/м2 или мегапаскалях МПа = 106 Па.

Разложим вектор R по осям координат на составляющие N,

Qx, Qy. Определим нормальные и касательные напряжения:

• нормальное напряжение

	σz = lim	N	= dN	;	(10.2)
		A
	A→0		dA

• касательные напряжения

		Qx			dQx
τyz =	lim		=				,
		A			dA
	A→0							(10.3)
		Qy					.
τyz =	lim			=	dQy
		A			dA
	A→0

Тогда величину напряжения p можно рассматривать как полное напряжение в точке на данной площадке (рис. 10.2).

p = σ2z + τ2xz + τ2yz .

(10.4)

Рис. 10.2

223

И. В. Богомаз. Механика

Но по разным направлениям площадок вблизи одной и той же точки напряжения будут иметь различные значения.

Совокупность нормального и касательных напряжений, действующих по различным площадкам, проходящим через данную точку, называется напряженным состоянием в этой точке.

Понятие напряжения является фундаментальным для всей механики деформируемого твердого тела. Вычисление напряжений является основой расчетов на прочность.

10.2. Интегральные зависимости между внутренними силовыми факторами и напряжениями

Пусть в некоторой точке элементарной площадки dA выявлены напряжения σz, τxz, τyz (рис. 10.2).

Внутренние усилия на элементарной площадке dA будут равны:

dN = σzdA, dQx = τxzdA, dQy = τyxdA .

Запишем моменты этих сил относительно осей координат Oxyz, связанных с dA, причем ось Oz параллельна нормали n :

dM x = σzdA y; dM y = σz d A x; dM z = τxzdA y −τyzdA x. (10.5)

Просуммируем элементарные внутренние усилия и их моменты по площади сечения А:

	N = ∫σzdA,	Qx = ∫τxzdA,	Qy = ∫τyzdA;
	A	A	A	(10.6)
	M x = ∫σz y dA, M y = ∫σz x dA, M z = ∫(τxz y −τyz x)dA.
	A	A	A

Выражения (10.5) называются интегральными уравнениями равновесия или статическими уравнениями.

Записанные статические уравнения не позволяют определить напряжения σ и τ, пока не установлен закон их распределения по сечению.

224

10. Понятие о напряжении и деформации

10.3. Деформации и перемещения. Деформированное состояние в точке

Изменение формы и размеров тела в результате внешнего воздействия (нагрузка, температура и другое) называется деформацией.

Положение каждой точки тела определяется ее радиус-вектором r {x, y, z} в системе координат Oxyz. При деформировании тела все

его точки смещаются.

Под влиянием приложенных сил твердое тело деформируется. Смещение во взаимном расположении частиц материала, соответствующее деформации, сопровождается изменением внутренних сил взаимодействия между частицами, при этом они являются непрерывными функциями точек тела.

Рассмотрим определенную точку. Если ее радиус-вектор до деформации был r {x1, x2 , x3}, то в деформированном теле он будет

иметь другое значение: r {x2 , y2 , z2} (рис. 10.3).

Смещение точки тела при деформировании будет определено вектором деформации (вектором смещения), который обозначим

u = r2 −r1 .

Рис. 10.3

Выразим вектор деформации через его координаты u {ux ,uy ,uz },

где ux, uy, uz – координаты вектора деформации u по осям декартовой системы координат.

225

И. В. Богомаз. Механика

Рис. 10.4

Тогда (рис. 10.4)

u = ux i +uy j +uz k ,

где i , j , k – единичные орты.

Рассмотрим случай, когда деформация по всему телу постоянна, например, растянули балку длиной A вдоль оси балки центральными силами на величину A.Тогда перемещение точки с координатой x пропорционально самому перемещению x, т. е. A ≈ x . Введем определение относительной линейной деформации. Для этого обозначим пе-

ремещение точки А по оси Ox через					хA. Разделим		хA на длину
стержня, получим			ux
	xA	≈		→ux =	xA	x .	(10.7)
	A		x
					A

Введем обозначение

AxA = εxx .

Здесь εxx – относительная линейная деформация точки А в направлении оси Ox.

Перепишем (10.7) и получим

ux = εxxx.

Если деформация неоднородна, то связь между x и ux будет меняться от точки к точке. Следовательно, относительную линейную деформацию εxx запишем как локальную величину

εxx =	∂u(x, y, z)	≡	∂u .
	∂x		∂x

226

10. Понятие о напряжении и деформации

Тогда растяжения по осям Oy и Oz будут описываться величи-

нами

εyy =	∂u(x, y, z)	≡	∂u	, εzz =	∂u(x, y, z)	≡	∂u .
	∂y		∂y		∂z		∂z

Тогда перемещение вектора деформации u = ux i +uy j +uz k можно записать как дифференциал

числяется по формуле

dR = Rxdx + Rydy + Rzdz,

где

R = ∂R			=	lim	R(x + x, y, z) − R(x, y, z) ;
	x	∂x				x
				x→0
Ry =		∂R	= lim		R(x, y +	y, z) − R(x, y, z) ;
du =		∂y		y→0		y
	R = ∂R		=	lim	R(x, y, z + z) − R(x, y, z) .
	x	∂z				z
				z→0
	∂u dx +		∂u dy		+ ∂u dz = εxxdx +εyydy +εzzdz .
	∂x		∂y		∂z
Полный дифференциал					dR векторной функции R{x, y, z}вы-

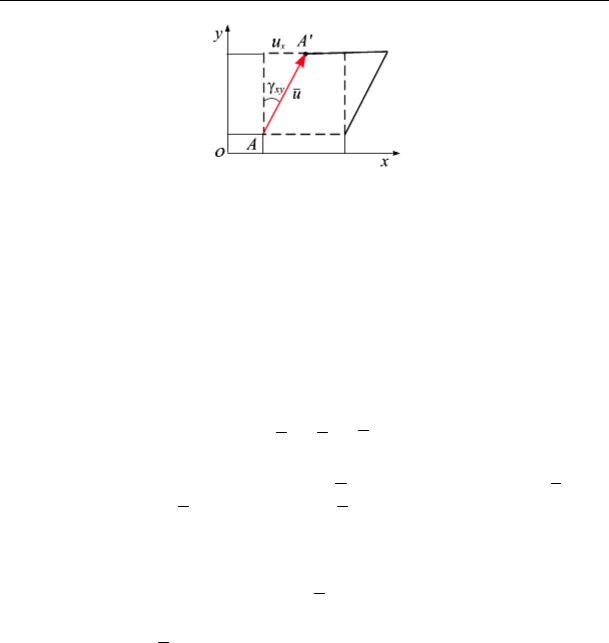
Введем понятие угловой деформации или, как принято говорить, деформации сдвига. При этой деформации точка будет перемещаться под углом к направлению оси Ox, например, в плоскости Oxy (рис. 10.5). При такой деформации перемещение в направлении оси Ox каждой частицы пропорционально ее перемещению вдоль оси Oy,

т. е. углу γyx. Тогда

tg γxy = uyx , при γxy 1 имеем γxy = uyx →ux = γxy y.

227

И. В. Богомаз. Механика

Рис. 10.5

Таким образом, деформацию сдвига плоскости Oxy в каждой точке можно записать

ux = γxyy, uy = γxyx.

При деформировании тела меняются расстояния между его точками. Вычислим удлинение отрезка dS, направление которого задано единичным вектором

ν = Ai + mj + nk .

Скалярное умножение вектора du на единичный вектор ν дает проекцию вектора du на направлениеν .

Определим относительную деформацию произвольно направ-

ленного волокна тела, как

ευ =

d

u

υ

.

(а)

Вычислим d

u

υ:

dS

∂u

x

∂uy

∂u

∂u

x

∂uy

∂u

du υ =

i

+

j

+

z k

dx +

i +

j +

z k dy +

∂x

∂x

∂x

∂y

∂y

∂y

∂u

∂uy

∂u

x i

(Ai

+ mj + nk )=

+

+

j +

z k dz

∂z

∂z

∂z

∂u

x A

∂uy

∂u

∂u

x

∂uy

∂u

=

+

m +

z n dx +

A+

m +

z n dy +

∂x

∂y

∂x

∂x

∂y

∂y

228

10. Понятие о напряжении и деформации

∂u

x A

∂uy

∂u

z

∂u

x

A2

∂uy

m2

∂u

z n2

+

+

m +

n dz

=

+

+

+

∂z

∂z

∂z

∂z

∂z

∂z

∂uy

∂u

∂u

∂u

∂uy

∂u

+

+

x Am +

z +

x

An +

+

z mn.

∂x

∂x

∂y

∂x

∂z

∂y

Вычислим относительную деформацию (а):

ευ =

d

u

υ

=

∂u

x A

+

∂uy

m

+

∂u

z

n

dx

+

dS

∂x

∂x

∂x

dS

∂u

x A+

∂uy

∂u

z n

dy

∂u

x A+

∂uy

∂u

z

dz

+

m +

+

m +

n

=

∂y

∂z

∂y

∂y

dS

∂z

∂z

dS

∂u

x A

∂uy

∂u

z

∂u

x A+

∂uy

∂u

z

=

+

m

+

n A

+

m +

n m

+

∂x

∂y

∂x

∂x

∂y

∂y

∂u

x A

∂uy

∂u

z

+

+

m

+

n n

=

∂z

∂z

∂z

=

∂u

x

A2

+

∂uy

mA+

∂u

z

nA+

∂u

x

Am +

∂uy

m2 +

∂u

z nm +

∂x

∂y

∂x

∂x

∂y

∂y

∂u

∂uy

∂u

z n2 =

∂u

A2

∂uy

m2 +

∂u

n2

∂uy

∂u

+

x An +

mn +

x

+

z

+

+

x nA+

∂z

∂y

∂x

∂z

∂z

∂x

∂z

∂y

∂u

z +

∂u

x

∂u

z +

∂uy

+

nA+

nm.

∂z

∂x

∂z

∂y

Введем обозначения:

εx =

∂u

x

;

εy =

∂uy

;

εz

=

∂u

z ;

∂z

∂z

∂z

229

И. В. Богомаз. Механика

∂uy

∂u

∂u

∂u

∂uy

∂u

γxy =

+

x

;

γxz =

z

+

x

;

γyz =

+

z .

∂x

∂x

∂y

∂x

∂z

∂y

Относительная деформация произвольно направленного волокна тела

ευ = εxA2 + εy m2 + εz n2 + γxyAm + γxyAn + γxy mn.

Здесь три скалярные величины εx, εy, εz имеют смысл относительных продольных деформаций, скалярные величины γxy, γxz, γzy имеют смысл относительных деформаций сдвига.

Совокупность линейных и угловых деформаций по различным направлениям и плоскостям для одной точки называется деформированным состоянием в этой точке.

Практически почти во всех случаях деформирования тел деформации оказываются малыми. Другими словами, относительные удлинения малы по сравнению с единицей.

Определение деформаций связано с расчетом на жесткость

ивыяснением законов распределения напряжений в брусе при различных нагружениях. Различают простые деформации – растяжение или сжатие, сдвиг, кручение, изгиб – и сложные, состоящие из двух

иболее простых деформаций.

Рис. 10.6

230

10. Понятие о напряжении и деформации

В зависимости от свойств материала и величины нагрузок деформации бывают упругие, полностью исчезающие после удаления нагрузок, и пластические или остаточные, неисчезающие, остающиеся после удаления нагрузок.

При исследовании напряженно-деформированного состояния используют различные программные продукты, например, программу MAV. Structure, предназначенную для численного анализа напряжен- но-деформированного состояния17 (рис. 10.6).

17 http://mav-structure.narod.ru/index.htm http://mav-structure.narod.ru/index.htm

231