6. Задание на дом.

6.1. Практика:

6.1.1. Случайная величина Х задана функцией распределения:

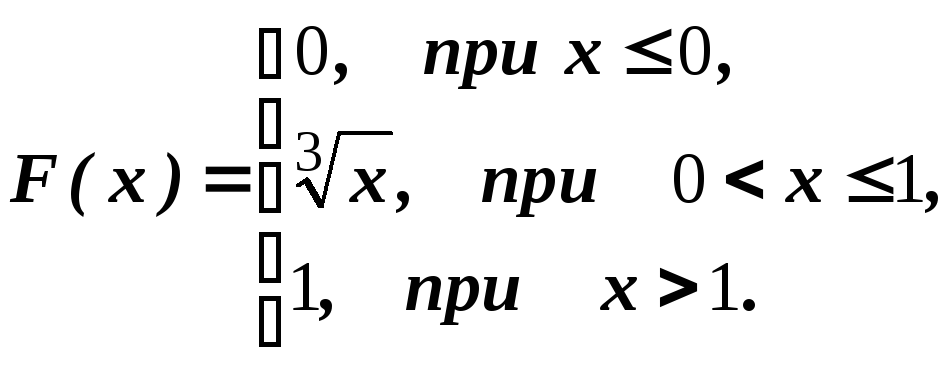
1) Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0, 1).

2) Найти функцию плотности распределения вероятностей.

6.1.2. Случайная величина Х задана функцией распределения.

Найти функцию плотности распределения вероятностей.

6.1.3. Построить функцию распределения для дискретной случайной величины, заданной законом распределения:

x	3	4	7	10
p	0,2	0,1	0,4	0,3

6.2. Теория.

6.2.2. Лекция по теме: «Числовые характеристики непрерывной случайной величины. Нормальный закон распределения.

6.2.2. Лобоцкая и др. С.162-169.

1. Тема: Числовые характеристики непрерывных случайных величин. Нормальный закон распределения

2. Актуальность темы: непрерывные случайные величины имеют широкое применение при решении естественнонаучных задач.

3. Цель занятия: закрепить понятие непрерывных случайных величин, закона распределения дискретной случайной величины и характеристик распределения.

3.1. Целевые задачи:

знать: определение непрерывной случайной величины, определение интегральной функции распределения, функции плотности распределения непрерывной случайной величины; числовые характеристики распределения; нормальный закон распределения.

уметь: вычислять характеристики распределения непрерывной случайной величины; находить вероятность попадания нормально распределенной случайной величины в заданный интервал.

4. Краткие сведения из теоретического курса Характеристики непрерывных случайных величин

Пусть непрерывная случайная величина Х задана плотностью распределения f(x) на отрезке [a, b].

Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a, b], называется определенный интеграл:

.

Введем понятие дисперсии для непрерывной случайной величины, заданной

Дисперсией непрерывной случайной величины X называется математическое ожидание квадрата отклонений, если возможные значения принадлежат отрезку [a, b]:

.

Замечание. Для вычисления дисперсии непрерывной случайной величины удобно пользоваться формулой:.

Среднее квадратическое отклонение непрерывной случайной величины определяется также как и для дискретной случайной величины:

.

Нормальное распределение

Нормальным называется распределение вероятностей случайной величины, которое описывается плотностью

.

Нормальное распределение определяется двумя параметрами  и ,  – математическое ожидание,  – среднее квадратическое отклонение.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Функция f(x) определена на всей оси х, при всех значениях хнормальная кривая расположена над осью Ох.Ось Охслужит горизонтальной асимптотой графика (рис. 6.1.); при функция имеет максимум, равный

Рис.6.1. Кривая Гаусса при

Влияние параметров нормального распределения на форму нормальной кривой

Изменение величины параметра  (математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ох: вправо, если  возрастает, и влево, если  убывает.

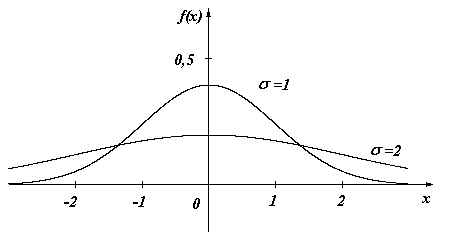
Рис. 6.2

Если изменяется параметр (среднее квадратическое отклонение). Так как максимум дифференциальной функции нормального распределения равен . Отсюда следует, что с возрастанием  максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, т. е. сжимается к оси Ох; при убывании  нормальная кривая становится более островершинной и растягивается в положительном направлении оси Оу (рис.6.2). Подчеркнем, что при любых значениях параметров  и  площадь, ограниченная нормальной кривой и осью х, остается равной единице.