6. Задание на дом

6.1. Теория.

6.1.1. Лекция по теме «Математические методы оптимизации»

6.1.2. Лобоцкая и др. С.250-260.

1. Тема: Задачи линейного программирования

2. Актуальность темы: методы оптимизации используются при решении задач распределения поставок, планирования производства, составления оптимального рациона питания и др.

3. Цель занятия: решать задачи линейного программирования графическим методом.

3.1. Целевые задачи:

знать: постановку задачи линейного программирования; типы задач линейного программирования; перевод задачи на математический язык; суть графического метода решения задачи линейного программирования;

уметь: решать графически системы неравенств; решать системы линейных уравнений; записывать задачу на математическом языке, постро­ить область допустимых значений, найти оптимальный план.

4. Краткие сведения из теоретического курса

Математические методы оптимизации применяются при решении задач распределения ресурсов, планирования производства, распределения запасов и перевозок. Суть их заключается в том, что из множества вариантов нужно выбрать оптимальный.

Для решения задач оптимизации разработано несколько методов. Во многих случаях решение задачи сводится к отысканию максимума или минимума некоторой функции. Такая функция называется целевой или функцией цели.

Дадим общую формулировку задачи линейного программирования.

Пусть переменные х₁, х₂, х₃…х_n– определяют рассматриваемый процесс. Эти переменные должны удовлетворять некоторым условиям, выраженным в виде системы линейных уравнений или неравенств. Для записи этих уравнений или неравенств в общем виде воспользуемся буквенной символикой (а_ij – коэффициенты). Тогда систему ограничений можно записать:

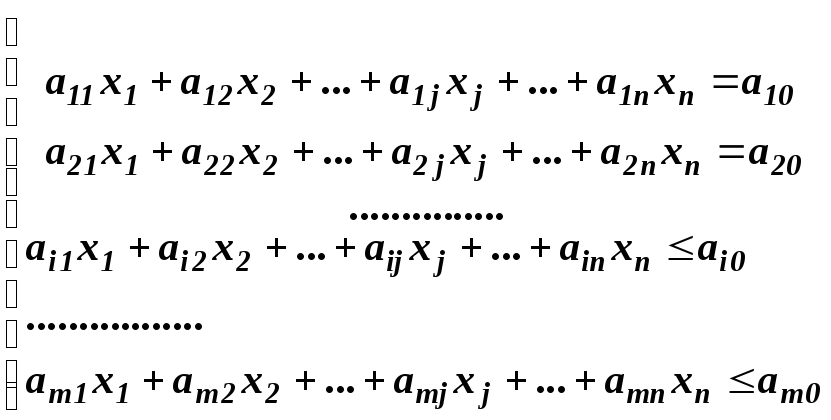
Кроме этих общих ограничительных условий, в задачах линейного программирования фигурируют еще условия неотрицательности: х₁0, х₂0,… х_n0.

Любая совокупность значений х₁, х₂, х₃…х_n, удовлетворяющих системе и условиям определяет один из допустимых вариантов процесса. В общем случае их будет бесчисленное множество. Каждый из этих вариантом характеризуется величиной:

,

где х_i – переменные, удовлетворяющие системе неравенств, с_i – постоянные числа.

Конечной целью исследования является определение такого допустимого варианта решения, для которого функция h (целевая функция) принимает оптимальное (наибольшее или наименьшее) значение.

Итак, формулировка задачи линейного программирования: найти совокупность значений n переменных х₁, х₂, х₃…х_n, удовлетворяющих системе ограничительных условий, условиям неотрицательности и для которых целевая функция принимает наибольшее (или наименьшее) значение.

Совокупность значение х₁, х₂, х₃…х_n , удовлетворяющих системе ограничений, называется допустимым решением, а допустимое решение, для которого функция принимает наибольшее или наименьшее значение – оптимальным решением задачи линейного программирования.

Графический метод решения задачи линейного программирования

Графический метод решения задач линейного программирования, как будет видно из дальнейшего, имеет весьма ограниченную область применения (не более двух переменных). Однако, несмотря на это, он оказывается весьма полезным для демонстрации общих идей, лежащих в основе других методов, для придания им необходимой наглядности.

Рассмотрим этот метод применительно к следующей задаче:

Задача. Найти решение , удовлетворяющие системе неравенств

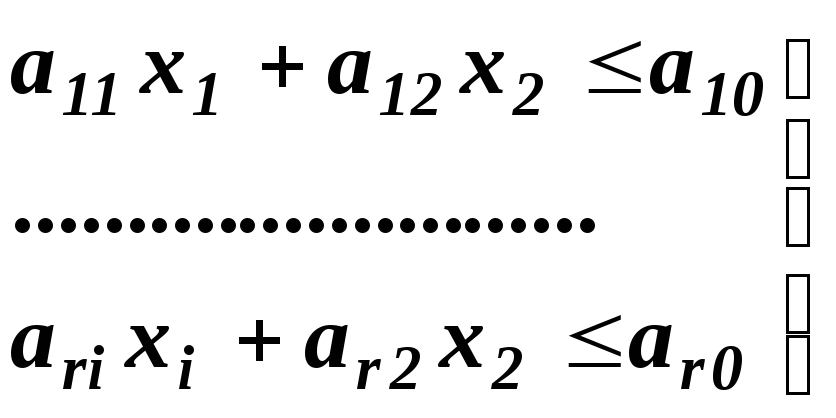
и условиям неотрицательности x_i0; x₂0,

для которых функция z=c₁x₁+c₂x₂ достигает максимума.

Построим прежде всего в системе координат х₁Ох₂ область допустимых решений задачи. Для этого, заменив каждое из неравенств равенством, строим соответствующую ему граничную прямую a_i1x₁+ a_i2x₂=a_i0 (для i=1, 2, …, r). Эта прямая делит плоскость х₁Ох₂ на две полуплоскости. Для координат х₁, х₂ любой точки А одной полуплоскости выполняется неравенство a_i1x₁+ a_i2x₂a₁₀, а любой точки В другой полуплоскости – противоположное неравенство a_i1x₁+ a_i2x₂a₁₀. Координаты любой точки граничной прямой удовлетворяют уравнению a_i1x₁+ a_i2x₂=a_i0.

Для определения, по какую сторону от граничной прямой располагается полуплоскость, соответствующая заданному неравенству, достаточно «испытать» одну какую-нибудь точку (проще всего точку О (0, 0)). Если при подстановке её координат её левую часть неравенства оно удовлетворяется, то полуплоскость обращена в сторону к «испытуемой» точке, если же неравенство не удовлетворяется, то соответствующая полуплоскость обращена в противоположную сторону. Направление полуплоскости показывается на чертеже штриховкой. Неравенствам x₁0 и x₂0 также соответствуют полуплоскости, расположенные справа от оси ординат и над осью абсцисс. На рисунке строим граничные прямые и полуплоскости, соответствующие всем неравенствам. Общая часть («пересечение») всех этих полуплоскостей будет представлять собой область допустимых решений системы неравенств.

Теперь перейдём к графическому изображению целевой функции. Уравнение целевой функции при фиксированном значении h определяет прямую, а при изменении h– семейство параллельных прямых с параметром h. Очевидно, задача отыскания допустимого решения системы, для которого функция h достигает максимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наибольшему значению параметра h.

Задача отыскания допустимого решения системы, для которого функция h достигает минимума, геометрически сводится к определению в области допустимых решений точки, через которую пройдет линия уровня, соответствующая наименьшему значению параметра h.

Построим опорную линию: функция цели при h=0 (минимально возможное значение). Найдем оптимальное решение.

Таким образом, искомое оптимальное решение соответствует точке области допустимых решений, координаты которой можно определить путём совместного решения двух уравнений.

Если оптимальное решение задачи существует, то оно достигается, по крайней мере, в одной из вершин области допустимых решений.

Решение задач

1. Для изготовления изделий двух видов №1 и №2 имеется не более 100 кг сырья. На изготовление одного изделия №1 расходуется 2 кг сырья, а изделия №2 – 4 кг. Составить план производства, обеспечивающий получение наибольшей выручки от продажи изделий, если отпускная стоимость одного изделия №1 установлена 3 руб., а изделия №2 – 2 руб., причем изделий №1 требуется изготовить не более 40, а изделий №2 – не более 20.

2. Содержание витаминов А и С в одном килограмме вишни составляет соответственно 3 мг и 150 мг, а в одном ки­лограмме абрикос - 24 и 75 мг. Сколько кг вишни и абрикос сле­дует взять в дневной рацион, чтобы потребить не менее 6 мг витамина А и не менее 75 мг витамина С при минимальных затратах, если 1 кг вишни стоит 4 рубля, а абрикос 5 рублей.