
- •Тема 1. Фізичні основи механіки. Кінематика Лекція 1. Основи кінематики поступального та обертального рухів Основні визначення
- •Швидкість і прискорення
- •Кінематика обертального руху
- •Лекція 2. Основи динаміки матеріальної точки та абсолютно твердого тіла Перший закон Ньютона.
- •Сила. Маса. Другий закон Ньютона.
- •Третій закон Ньютона.
- •Сили тертя
- •Сили пружності. Закон Гука.
- •Імпульс. Закон збереження імпульсу
- •Реактивний рух
- •Момент імпульсу. Закон збереження моменту імпульсу
- •Обертальний рух матеріальної точки відносно нерухомої осі
- •Теорема Штейнера (Гюйгенса)
- •Лекція 3. Робота. Енергія. Потужність
- •Робота при обертальному русі.
- •Закони збереження енергії в механіці
- •Потужність
- •Електростатичне поле та його характеристики
- •1. Електричний заряд. Закон збереження електричного заряду замкненої системи
- •2. Закон Кулона
- •3. Електростатичне поле та його напруженість. Лінії напруженості поля
- •4. Робота сил електростатичного поля по переміщенню точкового заряду
- •5. Потенціал електростатичного поля
- •6. Різниця потенціалів. Принцип суперпозиції електростатичних полів
- •7. Еквіпотенциальні поверхні
- •Лекція 05 Теорема Остроградського-Гаусса
- •Теорема Остроградського-Гауса для електростатичного поля у вакуумі
- •1. Поле рівномірно зарядженої нескінченної площини
- •2. Поле рівномірно зарядженої сферичної поверхні
- •3. Поле об'ємно зарядженої кулі
- •4. Поле рівномірно зарядженого нескінченного циліндра (нитки)
- •2. Поляризація діелектриків. Вектор поляризації
- •3. Лінії електричного зміщення і потік електричного зміщення.
- •Потік електричного зміщення для замкненої поверхні
- •4. Теорема Остроградського-Гаусса для електростатичного поля в діелектриці
- •5. Сегнетоелектрики, їх властивості та використання
- •Провідники в електричному полі
- •Електростатична індукція
- •Електрична ємність відокремленого (самотнього) провідника
- •Конденсатори, їх типи та ємність
- •Лекція 08 Постійний електричний струм
- •1. Електричний струм та його характеристики (сила, густина струму).
- •Умови існування електричного струму
- •Сторонні сили. Електрорушійна сила і напруга
- •Закон Ома
- •Опір і провідність провідників
- •Робота та потужність електричного струму
- •Правила Кірхгофа для розгалужених кіл
- •Під час розрахунку складних кіл із застосуванням правил Кірхгофа необхідно:
- •Лекція 09. Магнітне поле постійного струму Загальний опис магнітного поля
- •2. Потік вектора магнітної індукції. Теорема Остроградського-Гаусса для поля в
- •Магнітний потік крізь довільну поверхню s
- •3. Закон Біо-Савара-Лапласа та приклади його застосування (визначення індукції магнітного поля прямолінійного провідника зі струмом і магнітне поле в центрі кругового струму)
- •4. Теорема про циркуляцію векторів магнітної індукції та напруженості магнітного поля
- •Дія магнітного поля на рухомі заряди
- •1. Магнітне поле рухомого заряду
- •2. Дія магнітного поля на рухомий заряд. Сила Лоренца
- •3. Рух зарядженої частинки в магнітному полі
- •4. Формула Ампера
- •Робота по переміщенню контуру із струмом. Робота dА сил Ампера при даному переміщенні контуру (рис. 10.7) дорівнює сумі робіт по переміщенню провідників авс (dА1) і cda (dА2), тобто
- •Магнітне поле в речовині
- •1. Магнітний момент електрона і атома
- •2. Типи магнетиків
- •Намагніченість. Магнітне поле в речовині Намагніченість – це фізична величина, яка визначається магнітним моментом одиниці об'єму магнетика:
- •Феромагнетики та їх властивості Феромагнетики
- •1. Явище електромагнітної індукції. Закон Фарадея. Правило Ленца Досліди Фарадея і наслідки з них.
- •Індуктивність нескінченно довгого соленоїда. Соленоїд – це згорнутий в спіраль ізольований провідник, по якому протікає електричний струм. Повний магнітний потік соленоїда (потокозчеплення)
- •4. Енергія та об'ємна густина енергії магнітного поля
- •1. Коливання та їх типи
- •2. Механічні вільні гармонічні коливання, їх диференціальне рівняння та розв'язок
- •3. Енергія гармонічних коливань
- •Кінетична енергія
- •4. Електричний коливальний контур. Диференціальне рівняння власних електричних коливань та його розв'язок
- •Додавання гармонічних коливань
- •1. Метод векторних діаграм
- •2. Додавання гармонічних коливань одного напрямку
- •3. Биття
- •4. Додавання взаємно перпендикулярних гармонічних коливань. Поняття про фігури Ліссажу
- •Згасаючі коливання
- •1. Згасаючі механічні коливання
- •Енергія гармонічних коливань
- •Вимушені коливання
- •3. Вимушені електромагнітні коливання, диференціальне рівняння і його розв'язок і характеристики
- •4. Електричний резонанс і його використання в техніці
- •Резонанс напруг – це явище різкого зростання амплітуди сили струму в контурі при збігу циклічної частоти зовнішньої змінної напруги з власною частотою 0 коливального контура.
- •Пружні хвилі
- •1. Хвильовий процес. Види хвиль. Хвильова поверхня, фронт хвилі. Промінь
- •2. Гармонічна хвиля та її характеристики
- •3. Принцип Гюйгенса
- •4. Рівняння плоскої та сферичної хвиль
- •4. Хвильове рівняння пружної хвилі
- •Рівняння Максвелла
- •1. Аналіз явища електромагнітної індукції. Вихрове електричне поле. Циркуляція вектора напруженості вихрового електричного поля
- •2. Струм зміщення. Закон повного струму. Друге рівняння Максвелла
- •3. Система рівнянь Максвелла для електромагнітного поля в інтегральній формі. Електромагнітне поле
- •4. Вихрові струми (струми Фуко). Скін-ефект
- •2. Диференціальне рівняння електромагнітної хвилі та його дослідження
- •3. Енергія електромагнітних хвиль (об'ємна густина, потік, вектор Умова-Пойнтінга)
- •4. Тиск електромагнітних хвиль. Імпульс електромагнітного поля
- •5. Шкала електромагнітних хвиль
- •Лекція 19 Інтерференція хвиль
- •3. Стоячі хвилі
- •Лекція 20 Дифракція хвиль
- •1. Закони геометричної оптики. Дифракція світла. Принцип Гюйгенса- Френеля
- •2. Дифракція в паралельних променях на щілині
- •Квантова теорія теплового випромінювання
- •1. Теплове випромінювання, його рівноважність, характеристики
- •По спектральній густині енергетичної світимості можна розрахувати інтегральну енергетичну світимість, підсумувавши по всіх частотах:
- •2. Абсолютно чорне тіло. Розподіл енергії в спектрі випромінювання абсолютно чорного тіла. Закони Кірхгофа і Стефана-Больцмана
- •3. Розподіл енергії в спектрі випромінювання абсолютно чорного тіла. Закон зміщення Віна
- •4. Квантова гіпотеза Планка. Формула Планка
- •Квантова теорія атома водню. Розвиток теорії Бора. Атоми із багатьма електронами
- •1. Спектр випромінювання атома водню. Серіальна формула
- •2. Постулати Бора. Борівська теорія атома водню
- •Набір можливих дискретних частот
- •3. Квантово-механічний опис атома водню
- •4. Квантові числа: головне, орбітальне і магнітне квантові числа. Правила відбору
- •5. Орбітальні механічний та магнітний моменти електрона
- •6. Спін електрона. Спінове квантове число
- •7. Принцип Паулі. Розподіл електронів в атомі за станами. Характерні квантові числа
- •Розподіл електронів в атомі підпорядковується принципу Паулі: в одному і тому ж самому атомі не може бути більше одного електрона з однаковим набором чотирьох квантових чисел n, l, ml I mz , тобто
- •Лекція 24 Хвильові властивості мікрочастинок
- •2. Деякі властивості хвиль де Бройля
- •Фазова швидкість фотона
- •3. Співвідношення невизначеностей Гейзенберга
- •4. Хвильова функція, її статистичний зміст та властивості. Статистичний (ймовірнісний) опис мікрочастинок за допомогою хвильової функції
- •Лекція 25 Рівняння Шредінгера та його застосування
- •1. Головне рівняння нерелятивістської квантової механіки
- •2. Стаціонарне рівняння Шредінгера
- •3. Рух вільної частинки
- •4. Мікрочастинка в одновимірній прямокутній "потенційній ямі" з нескінченно високими "стінками"
- •Власні функції:
- •Нормовані власні функції:
- •5. Проходження частинки через потенціальний бар'єр прямокутної форми. Тунельний ефект
- •Лекція 26 Зонна теорія твердих тіл
- •1. Кристалічні і аморфні тверді тіла. Кристалічна гратка
- •Характерною ознакою кристалічних тіл є кристалічні гратки.
- •3. Квантова теорія електропровідності металів
- •Напівпровідники
- •3. Зонна структура металів, діелектриків та напівпровідників
- •Валентна зона – це зона, повністю заповнена електронами. Утворюється з енергетичних рівнів внутрішніх електронів вільних атомів.
- •2. Функція розподілу Бозе – Ейнштейна
- •3. Функція розподілу Фермі – Дірака Ця функція визначається аналогічно функція розподілу Бозе – Ейнштейна і має такий вид:
- •4. Поняття про виродження систем частинок, що описуються квантовими статистиками
- •5. Поняття про виродження електронного газу в металах
- •Електропровідність металів
- •1. Класична теорія електропровідності металів
- •Виведення закону Ома
- •Закон Джоуля-Ленца
- •Закон Відемана-Франца
- •Труднощі класичної теорії
- •2. Квантова теорія електропровідності металів
- •Напівпровідники
- •Лекція 29 Власні напівпровідники
- •1. Власна провідність напівпровідників
- •2. Електронна домішкова провідність (провідність n-типу)
- •3. Діркова домішкова провідність (провідність р-типу)
- •4. Фотопровідність напівпровідників
- •Власна фотопровідність
- •Домішкова фотопровідність
- •Люмінесценція твердих тіл
- •Правило Стокса
- •2. Фізичні процеси, що відбуваються в р-п-переході
- •Провідність p-n-переходу
- •3. Напівпровідникові діоди
- •Точковий напівпровідниковий діод
- •Площинний напівпровідниковий діод
- •4. Напівпровідникові тріоди (транзистори)
- •1. Фотопровідність напівпровідників
- •Власна фотопровідність
- •Домішкова фотопровідність
- •Люмінесценція твердих тіл
- •Правило Стокса
- •2.2. Фізичні процеси, що відбуваються в р-п-переході
- •Провідність p-n-переходу
- •2.3. Напівпровідникові діоди
- •Точковий напівпровідниковий діод
- •Площинний напівпровідниковий діод
- •2.4. Напівпровідникові тріоди (транзистори)
- •Контактні явища в металах
- •1. Робота виходу електронів з металу у вакуум
- •2. Контакт двох металів по зонній теорії, контактна різниця потенціалів
- •3. Термоелектричні явища: Зеєбека, Пельтьє, Томсона та їх використання
- •Контакт електронного і діркового напівпровідників (р-п-перехід)
- •1. Електронно-дірковий перехід (р-п-перехід)
- •2. Фізичні процеси, що відбуваються в р-п-переході
- •Провідність p-n-переходу
- •3. Напівпровідникові діоди
- •Точковий напівпровідниковий діод
- •Площинний напівпровідниковий діод
- •4. Напівпровідникові тріоди (транзистори)
Лекція 25 Рівняння Шредінгера та його застосування
1. Головне рівняння нерелятивістської квантової механіки
Головне рівняння нерелятивістської квантової механіки було сформульоване в 1926 році Е. Шредінгером. Воно має такий вигляд:
![]() ,
,
де
![]() ,
,
![]() – маса частинки;
– маса частинки;
![]() – оператор Лапласа
– оператор Лапласа
![]() ,
,
![]() – уявна одиниця;
– уявна одиниця;![]() – потенційна функція частинки в силовому
полі;
– потенційна функція частинки в силовому
полі;
![]() – розшукувана хвильова функція частинки.
– розшукувана хвильова функція частинки.
Це рівняння доповнюється умовами, що накладаються на хвильову функції, а саме:
1) хвильова функція повинна бути скінченною, однозначною і неперервною;
2) похідні
![]() повинні
бути неперервними;
повинні
бути неперервними;
3) функція
![]() повинна
інтегруватися; ця умова в найпростіших
умовах зводиться до умови нормування
вірогідності.
повинна
інтегруватися; ця умова в найпростіших
умовах зводиться до умови нормування
вірогідності.
2. Стаціонарне рівняння Шредінгера
Для багатьох фізичних явищ,
що відбуваються в мікросвіті, головне
рівняння Шредінгера можна спростити,
виключивши залежність
![]() від часу. Тоді матимемо
стаціонарне рівняння
Шредінгера, тобто
рівняння Шредінгера
для стаціонарних
станів – станів з
фіксованими значеннями енергії.
В такому випадку силове
поле, в якому частинка рухається, буде
стаціонарним, тобто
від часу. Тоді матимемо
стаціонарне рівняння
Шредінгера, тобто
рівняння Шредінгера
для стаціонарних
станів – станів з
фіксованими значеннями енергії.
В такому випадку силове
поле, в якому частинка рухається, буде
стаціонарним, тобто
![]() має
смисл потенційній
енергії.
має
смисл потенційній
енергії.
Розв'язок рівняння Шредінгера
представимо у вигляді добутку двох
функцій, одна з яких є функцією тільки
координат, друга –
тільки часу, причому
залежність від часу виражається множником
![]() :
:
![]()
де
![]() – повна енергія частинки.
– повна енергія частинки.
Підставивши![]() в загальне рівняння Шредінгера, і
виконавши нескладні перетворення
отримаємо рівняння
Шредінгера для стаціонарних станів:
в загальне рівняння Шредінгера, і
виконавши нескладні перетворення
отримаємо рівняння
Шредінгера для стаціонарних станів:
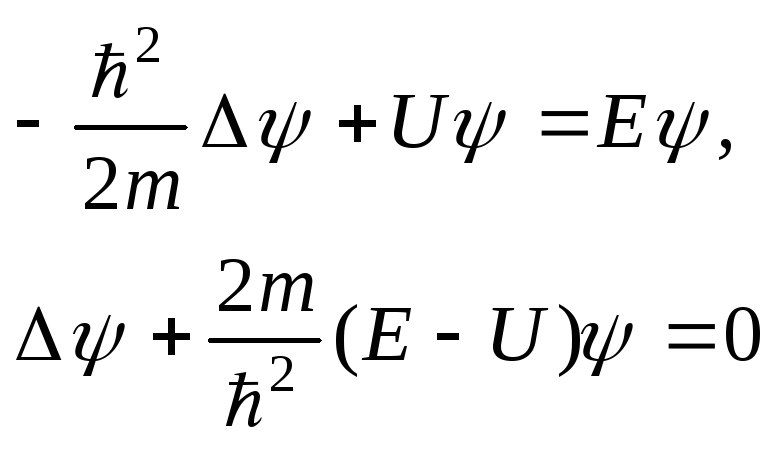 .
.
Наклавши граничні умови на розв'язок, відбирають рішення, що мають фізичний смисл. Для рівняння Шредінгера такими умовами є умови регулярності хвильових функцій: хвильові функції повинні бути скінченними, однозначними і неперервними разом зі своїми першими похідними.
Реальний
фізичний смисл мають
тільки такі розв'язки, які виражаються
регулярними функціями
![]() .
Проте регулярні розв'язки мають місце
не при будь-яких значеннях параметра
Е, а лише
при певному їх наборі, характерному для
даної задачі. Ці значення
енергії називаються
власними. Розв'язки,
які відповідають власним
значенням енергії,
називаються власними
функціями. Власні
значення Е
можуть утворювати як неперервний, так
і дискретний ряд. В першому випадку
говорять про неперервний спектр,
в
другому – про
дискретний
спектр.
.
Проте регулярні розв'язки мають місце
не при будь-яких значеннях параметра
Е, а лише
при певному їх наборі, характерному для
даної задачі. Ці значення
енергії називаються
власними. Розв'язки,
які відповідають власним
значенням енергії,
називаються власними
функціями. Власні
значення Е
можуть утворювати як неперервний, так
і дискретний ряд. В першому випадку
говорять про неперервний спектр,
в
другому – про
дискретний
спектр.
3. Рух вільної частинки
Розглянемо
рух
вільної частинки,
тобто
частинки, що рухається
у відсутність зовнішніх полів вздовж
осі
![]() .
Оскільки зовнішні сили на частинку не
діють, то її потенційна енергія
.
Оскільки зовнішні сили на частинку не
діють, то її потенційна енергія![]() і її можна прирівняти нулю.
В такому випадку рівняння
Шредінгера для стаціонарних станів
матиме вигляд:
і її можна прирівняти нулю.
В такому випадку рівняння
Шредінгера для стаціонарних станів
матиме вигляд:
![]()
Прямою підстановкою можна впевнитись, що частинним розв'язок цього рівняння є функція
![]() ,
,
де
![]() і
і![]() ,
з власними значеннями
,
з власними значеннями
![]() .
.
Залежна від часу хвильова функція
![]() ,
,
де позначено:
![]() .
.
Ця функція є плоскою монохроматичною хвилею де Бройля.
Густина вірогідності виявлення частинки в даній точці простору
![]()
не залежить від часу, тобто всі положення вільної частинки в просторі рівноімовірні.
Енергетичний спектр
вільної частинки.
З
формули
![]() витікає, що залежність енергії від
імпульсу
витікає, що залежність енергії від
імпульсу
![]()
є звичайною
для нерелятивістських частинок.
Енергія вільної частинки
може приймати будь-які значення (адже
хвильове число
![]() може приймати будь-які
позитивні, значення), тобто енергетичний
спектр вільної частинки
неперервний.
може приймати будь-які
позитивні, значення), тобто енергетичний
спектр вільної частинки
неперервний.
