3.4 Алгоритм максимизации выхода цилиндрического объёма брёвен

Изложенный выше метод раскряжевки хлыстов может быть реализован на ЭВМ. Рассмотрим это решение.

Функция (x)=0,25d²(х), представляет собой площадь сечения хлыста на некотором расстоянии х от его вершины (рис. 3.2). Если задана длина некоторого сортимента хлыста координатами х _i-1 и х_i, тогда произведение (х_i-х_i-1)(х_i-1 ), т.е. площадь ступеньки под функцией (х), будет равно цилиндрическому объёму соответствующего сортимента. Лучший в смысле максимума цилиндрического выхода раскрой хлыста на n сортиментов будет обеспечен выбором n-1узлов таких, чтобы площадь под ступенчатой функцией оказалась максимальной.

Рис.3.2 Пояснение к модели раскряжевки хлыстов

Площадь под ступенчатой функцией, расположенной под кривой (х), представляет собой функцию n-1 переменных x₁,...x_n-1,непрерывную на интервале [ а, b] , принимающую минимальные значения при х₁=…=х_n-1=a и x₁=...= x_n-1= b и имеющую максимум при a х₁… х_n-1 b. Условием максимума площади

(3.8)

под ступенчатой функцией является равенство нулю частных производных

при граничных условиях

(x₀)=(a)=const, x_n=b=const. (3.10)

Тогда максимум функции (3.8) получится путем её дифференцирования

Отсюда

(3.12)

Поскольку абсцисса начального узла х₀=а известна и соответственно значение функции в этом узле(х₀)=(а), то, если некоторое заданное значение очередной абсциссы х1 обеспечит в соответствии с (3.12) в конечном итоге вычислений всех х_i (i=1,...,n) значение х_n=b, задача решена. Если же окажется, что х_n > b или х_n< b, то соответственно и значение абсциссы х₁, необходимое для выполнения условий максимума площади под ступенчатой функцией, либо завышено, либо занижено. Эти математические выкладки позволяют построить простой итерационный алгоритм, последовательно уточняющий некоторое произвольно заданное значение абсциссы х₁ до такого, которое обеспечит нахождение всех оставшихся узлов, удовлетворяющих условиям (3.9)-(3.10).

Геометрически уравнение (3.11) представляет собой соотношение между катетами прямоугольного треугольника с координатами вершин , (рис.3.2), где Это обеспечивает возможность графического решения задачи: расстояние от уже известного узла х_i до следующего х_i+1 (катет, прилежащий углу ) определяется через разность между значениями функции в двух предыдущих узлах (x_i) и (x_i-1) (катет, противолежащий углу ) и значение производной (тангенс угла ).

Предложенный алгоритм может быть использован и для решения задачи максимизации цилиндрического выхода деловой древесины при раскряжевке хлыстов, имеющих центральную гниль.

3.5 Максимизациия цилиндрического объема брёвен при наличии центральной гнили

Предположим что образующая h = h(x) центральной гнили известна. Обозначим g(x)=0.25h²(x)-функцию, представляющую собой площадь сечения области гнили на расстоянии х от вершинного среза (рис.3.4). Для n сортиментов, получаемых из хлыста с центральной гнилью, необходимо будет выбрать расположение n-1 узлов так, чтобы обеспечить максимум площади фигуры, образованной ступенчатыми функциями под кривой (х) и над кривой g(х).

Площадь такой фигуры представляет собой функцию n-1 переменных x1,...,xn-1 непрерывную на интервале [а,b], принимающую минимальные значения при x1 =...= xn-1 = a и x1 =...= xn-1 = b и имеющую максимум при а< x1<...< xn-1 <b.

Рис.3.3 Модель раскряжевки хлыстов при наличии центральной гнили

Условием максимума площади

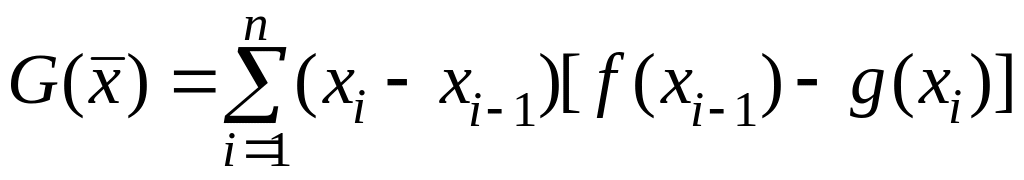(3.13)

ступенчатой фигуры является равенство нулю частных производных

при граничных условиях

x0=a, f(x0)=f(a), xn=b, g(xn)=g(b). (3.15)

Дифференцируя (3.13), получим

Уравнение (3.16) можно записать в виде системы:

которую можно решить с помощью изложенного выше алгоритма двойного итерационного процесса. Отметим также, что при реализации на ЭВМ предложенного алгоритма необходимо учитывать то обстоятельство, что функция определена, как правило, не на всем интервале [а, b].

С другой стороны, система (3.16) представляет собой систему n-1 нелинейных уравнений относительно х (i=1,...,n-1). Каждое из уравнений представляет собой непрерывно дифференцируемую действительную функцию переменных x_i-1, x_i, x_i+1. Данную систему также можно численно решить методом Ньютона. Итогом решения задачи максимизации выхода цилиндриче-

ского объёма сортиментов при раскряжевке древесного хлыста при наличии центральной гнили являются длины сортиментов, обеспечивающие максимум объёма деловой древесины, заключенной в кольцевом цилиндре. Блок-схема вычислительного алгоритма представлена на рис. 3.4. В блоке 1 осуществляется ввод исходных данных: диаметров раскраиваемого хлыста и центральной гнили. В диалоговом режиме происходит ввод порядка m аппроксимационных полиномов соответственно для образующей хлыста и образующей гнили, а также n-число раскраиваемых сортиментов. Во втором блоке производится расчет коэффициентов a₁ и b₁ функций d(x) и h(x) методом наименьших квадратов. В блоке 3 осуществляется проверка наличия гнили. Если гниль существует, то находим нуль функции g(x) (блок 4) методом бисекции. Эта точка является координатой g начала области гнили. На отрезке [0,g] от комля считаем, что g(x) = 0. Если центральной гнили нет, то g(x) = 0 на всем участке [0,1]. В блоке 5 находим координаты узлов х_i и длины сортиментов L(x_i). Расчет происходит методом двойной итерации, если гниль наличествует, и простой итерации, если она отсутствует. В блоке 6 производится вывод результатов раскроя на стандартные устройства вывода.

нет

^да

Рис.3.4 Алгоритм раскряжевки

хлыстов, имеющих центральную

гниль