4.3.3. Распределенные силы. Центр тяжести

До сих пор сила как мера взаимодействия материальных тел рассматривалась в виде вектора, приложен­ного к определенной точке тела. Однако в природе су­ществует широкий класс взаимодействий материальных тел, которые нельзя заранее представить в виде сосре­доточенного вектора, т. е. силы, приложенной к какой-то конкретной точке тела. Такими силовыми факторами являются, например, силы давления жидкостей и газов на твердые тела, силы тяготения, электромагнитные си­лы и т. д. Поэтому в механике вводятся в рассмотрение распределенные силы, которые делятся на поверхно­стные и объемные. Поверхностные действуют на каждый элемент поверхности рассматриваемого тела. Объемные действуют на каждый элемент объема рассматриваемого тела. К поверхностным силам относятся силы давления, а к объемным — силы тяготения и электромагнитные силы.

В теоретической механике все аксиомы и теоремы кинетики справедливы только при действии на механическую систему сосредоточенных сил. Поэтому при ис­пользовании этих теорем каждую распределенную на­грузку нужно заменить ее равнодействующей, то есть со­средоточенной силой. Такая замена правомерна, потому что в теоретической механике рас­сматриваются только абсолют­но твердые тела.

Р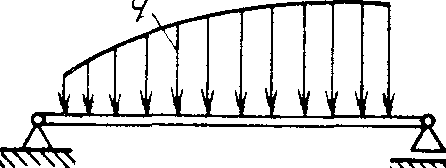 аспределенная нагрузка характеризуется ее интенсив­ностью, т. е. величиной силы, приходящейся: на единицу объема тела (в случае объ­емных сил), на единицу площади (в случае поверхност­ных сил), на единицу длины (в случае, когда можно пренебречь поперечными размерами тела). В последнем случае распределенная нагрузка называется плоской и на схеме изображается в виде

Рис. 4.22 графика интенсивности q, называемого эпюрой распределенной нагрузки (рис. 4.22). Направление взаимодействия между телами указывается стрелками, а кривая, ограничивающая эпюру, дает закон изменения интенсивности. На практике чаще всего встре­чаются параллельные распределенные силы одного на­правления. Рассмотрим наиболее важные с точки зрения практических приложений примеры распределенных сил этого вида: силы тяжести и плоскую распределенную нагрузку.

Центр тяжести твердого тела. На каждую частицу твердого тела, которое находится вблизи земной поверхности и размерами которого по сравнению с радиусом Земли можно пренебречь, действуют вертикальные силы тяжести (рис. 4.21). Как было выяснено выше (см. формулы 4.35 и 4.36), система этих парал­лельных сил имеет равнодействующую, модуль которой равен весу тела

. (4.37)

Эта равнодействующая направлена параллельно силам тяжести частиц тела, а координаты точки ее приложе­ния С — центра тяжести тела — определятся по фор­мулам

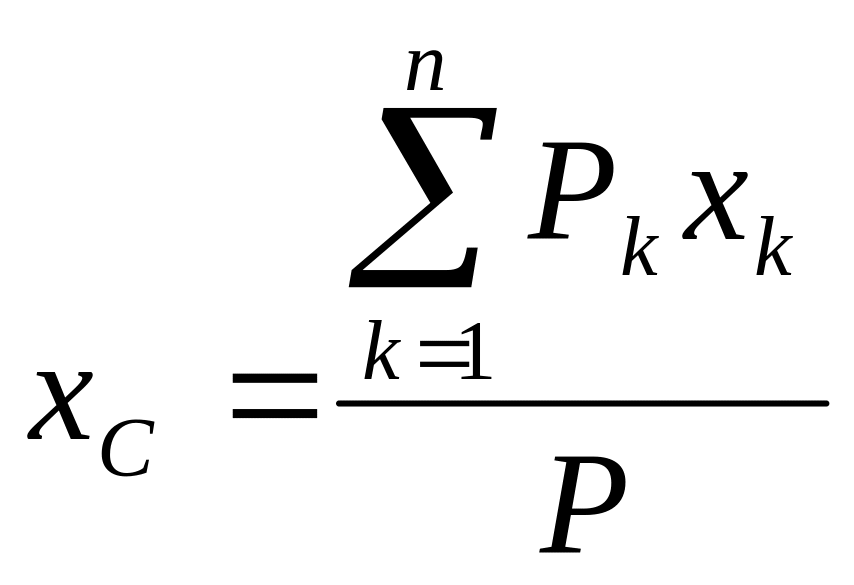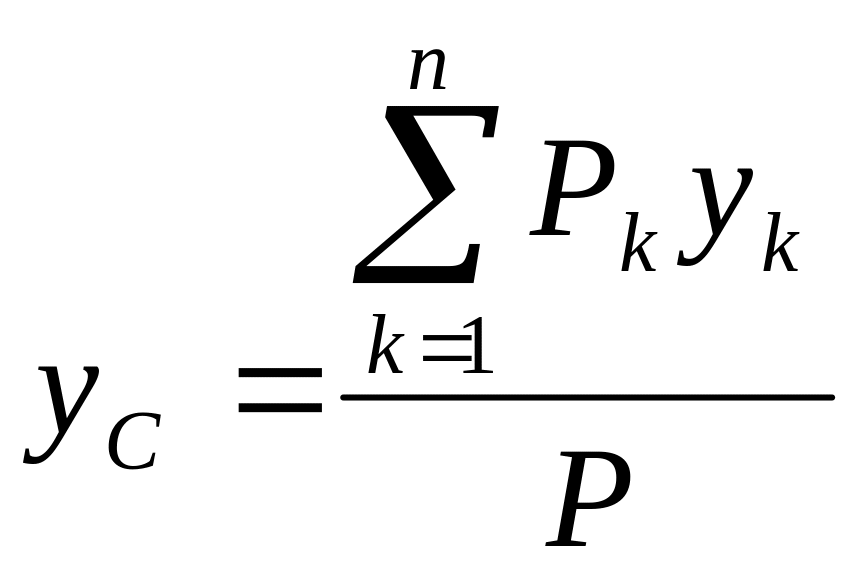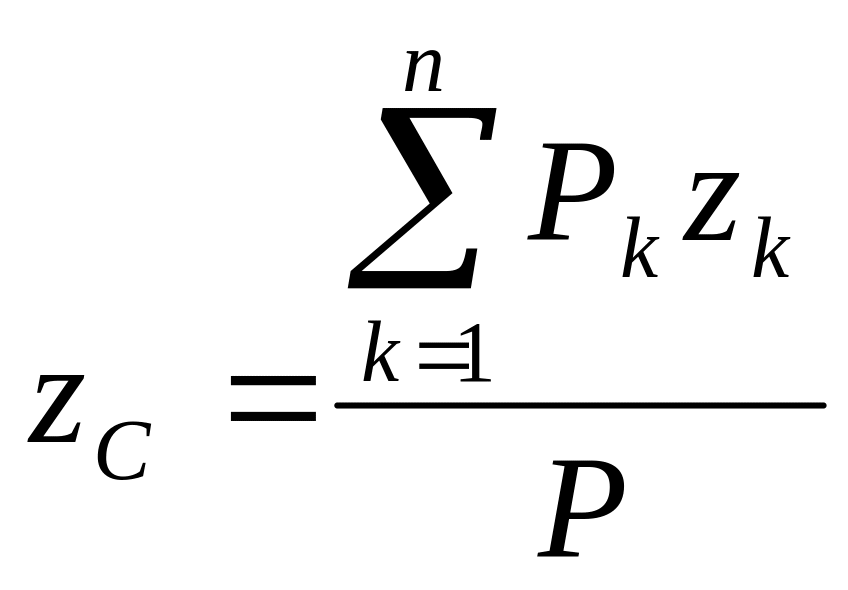, , , (4.38)

где х_k, у_k, z_k — координаты точек приложения сил тяжести P_к частиц тела.

Сила тяжести частицы тела равна массе этой частицы, умноженной на ускорение свободного падения:

P_k = m_kg. Если частица обладает объемом U_k, то ее масса т_k = ρ_kUk, где ρ_k — объемная плотность. В случае однородного тела, когда ρ_k = const, координаты центра тяжести определятся выражениями

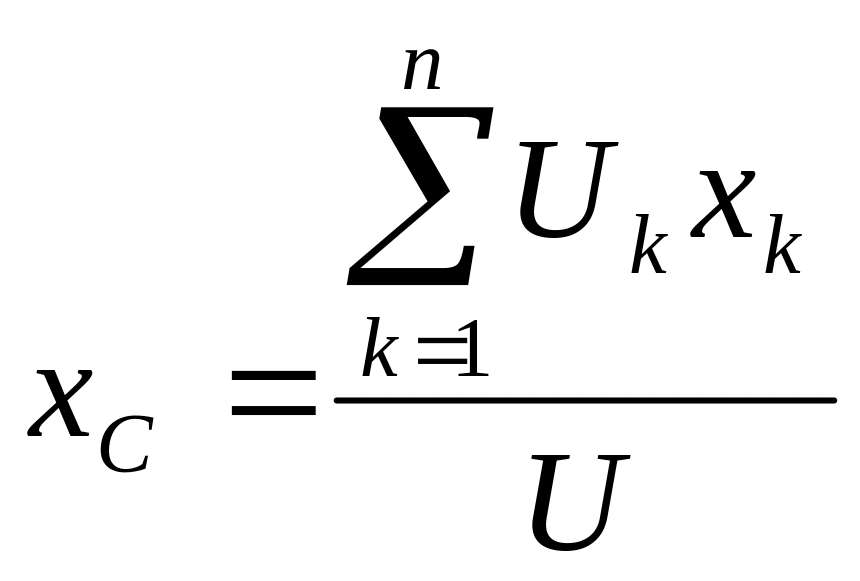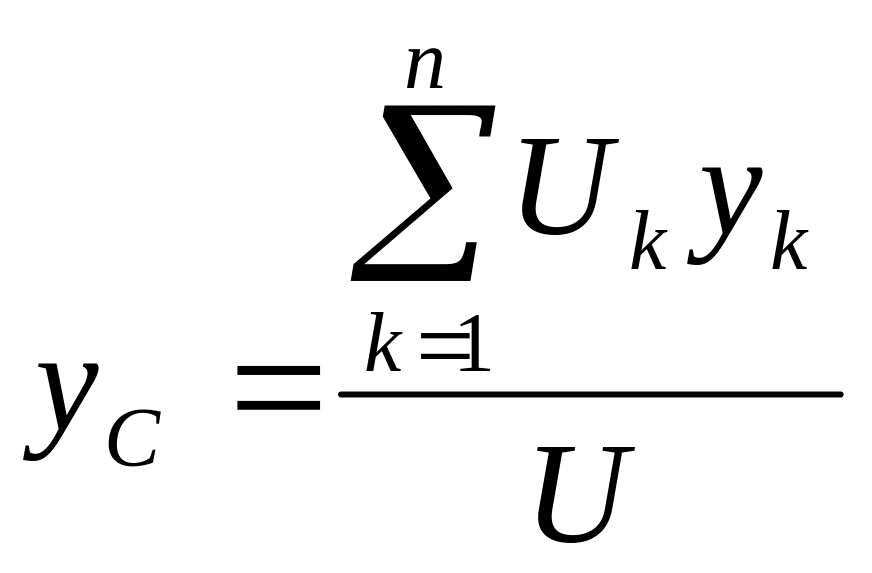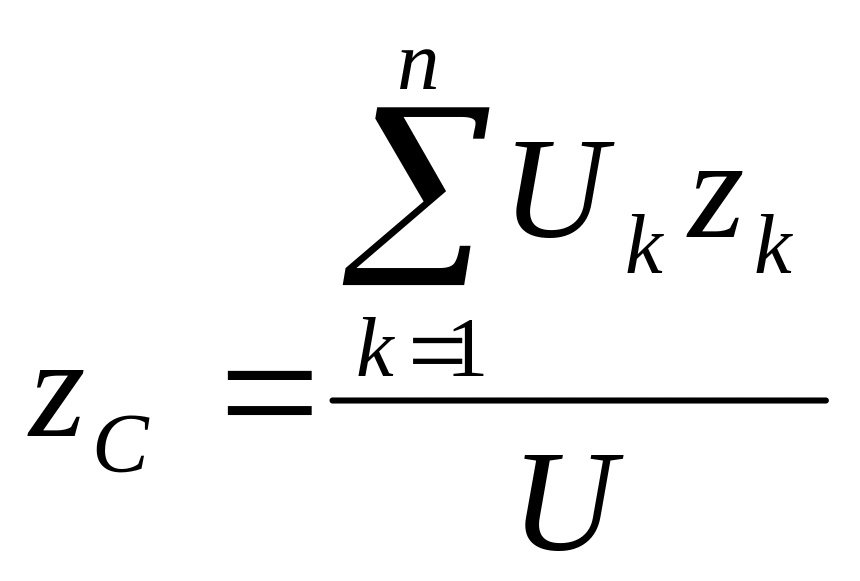, , , (4.39)

где — объем тела.

Если тело представляет собой однородную поверхность (оболочку), то , где ρ — поверхностная плотность, S_k — поверхность частицы, и тогда

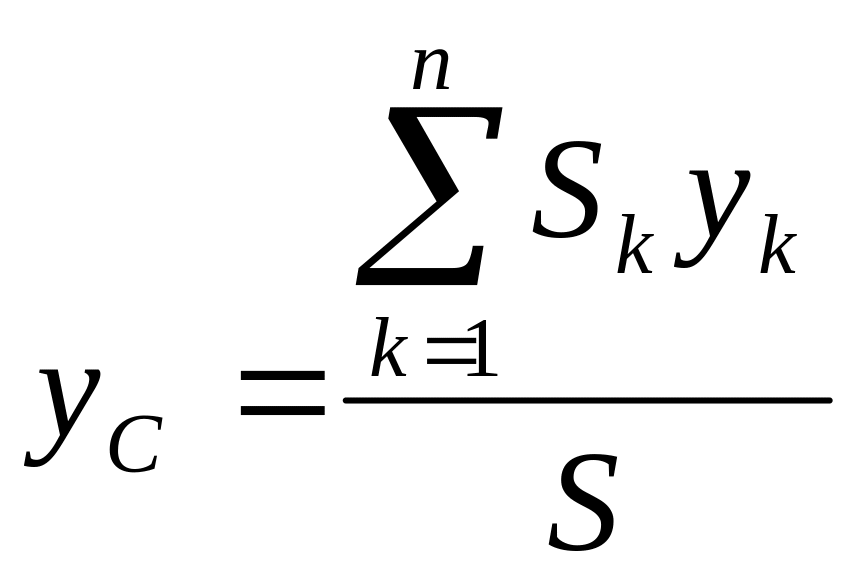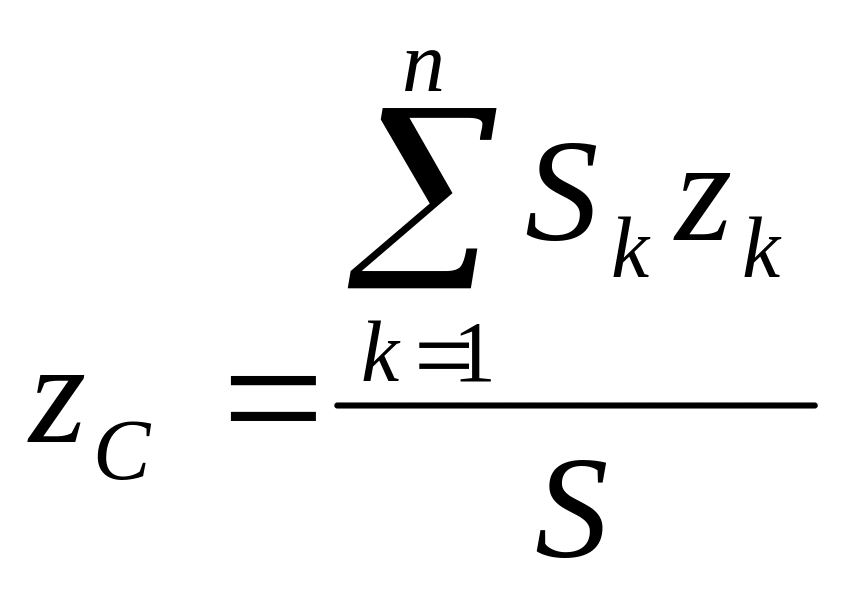, , , (4.40)

где S = ∑S_k — поверхность тела.

В случае однородной материальной кривой т_k = ρ_k, где ρ — линейная плотность, l_k— длина частицы, и тогда

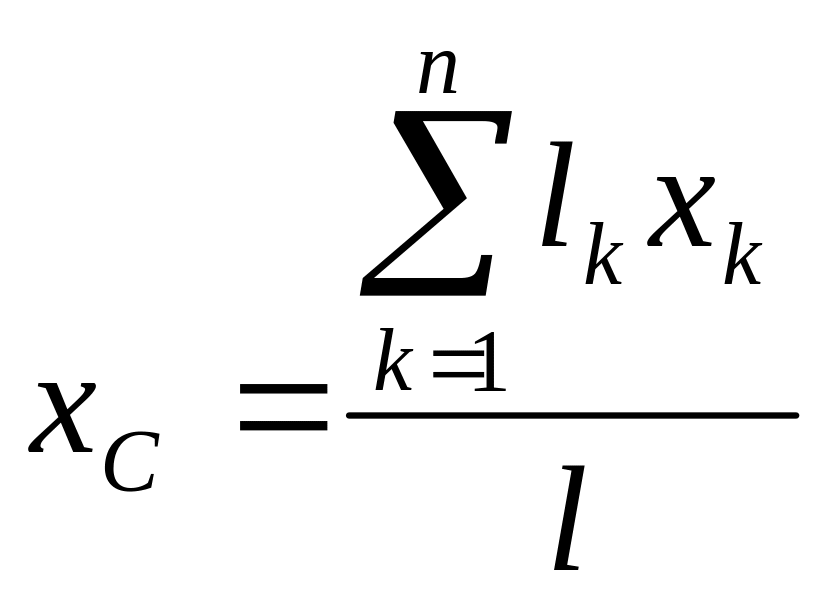, , , (4.41)

где l = ∑l_k — длина материальной линии. Все эти формулы служат основой для практических методов опреде­ления координат центра тяжести: метода интегрирования, разбиения и метода симметрии.

При использовании метода интегрирования тело раз­бивается на бесконечно малые частицы. Суммы в чис­лителях заменяются интегралами по объему, площади или длине тела.

Если же данное тело можно разделить на конечное число частей, веса и центры тяжести которых известны, то применяются непосредственно формулы (4,38)—(3.41); этот метод называется методом разбиения.

Суть метода симметрии заключается в том, что если материальное тело имеет плоскость, ось или центр ма­териальной симметрии, то его центр тяжести лежит в этой плоскости, на этой оси или в этом центре мате­риальной симметрии.

Пример 1. Определить центр тяжести однородной дуги окружности радиусом R с центральным углом 2α (рис. 4.23).

Р ешение. Так как дуга АВ имеет ось симметрии, то ее центр тяжести лежит на этой оси (ось Ох), и нам достаточно опре­делить ху. Длина бесконечно малого участка дуги равна

dl = R dφ,

а длина всей дуги. l = 2R α̣.. Заменив в формуле (4.41) сумму ин­тегралом,

Рис. 4.23 получим

.

Пример 2. Определить координаты центра тяжести однород­ной пластины, изображенной на рис. 4.24. (размеры указаны в сан­тиметрах).

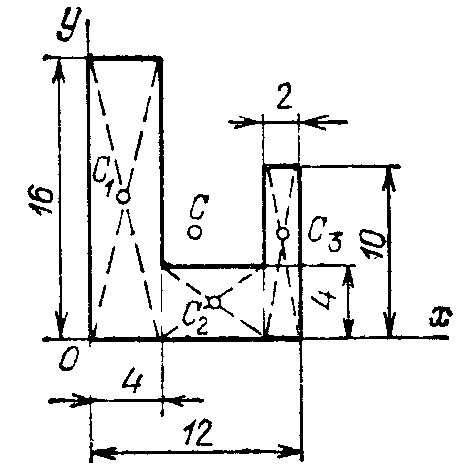
Решение. Проведем оси координат и разобьем пластину на три прямоугольника. Подсчитаем их площади и координаты их центров тяжести:

Рис. 4.24 S₁ = 64, x₁ =2, y₁= 8;

S₂ = 24, x₂ =7, y₂ =2;

S₃= 20, x₃ = 11, y₃ = 5.

Используя формулы (4.40), получаем

= cм,

= см.

Найденное положение центра тяжести С показано на рисунке 4.24.

Рассмотрим теперь плоскую распределенную нагрузку, интенсивность которой изменяется по закону q = f(х) (рис. 4.25). На элементарном участке длиной dx интенсивность нагрузки можно считать постоянной и распределенную нагрузку мож­но заменить сосредоточенной силой dQ = qdx. Тогда, заме­нив входящие в формулы (4.35) и (4.36) суммы интегралами, получим, что равнодействую­щая плоской распределенной нагрузки равна

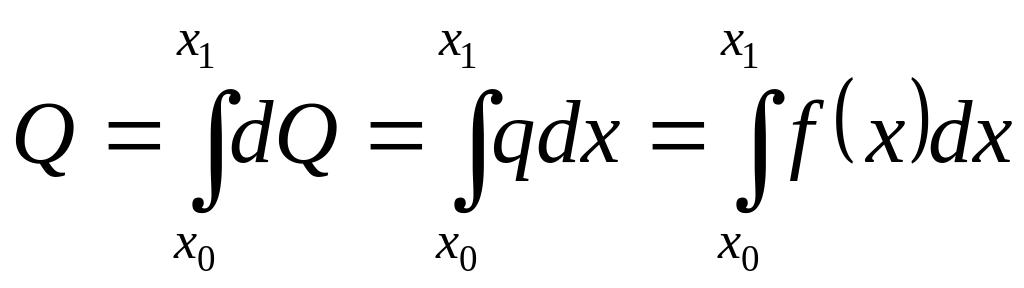(4.42)

п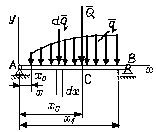 араллельна интенсивности распределенной нагрузки и приложена в точке С с

координатой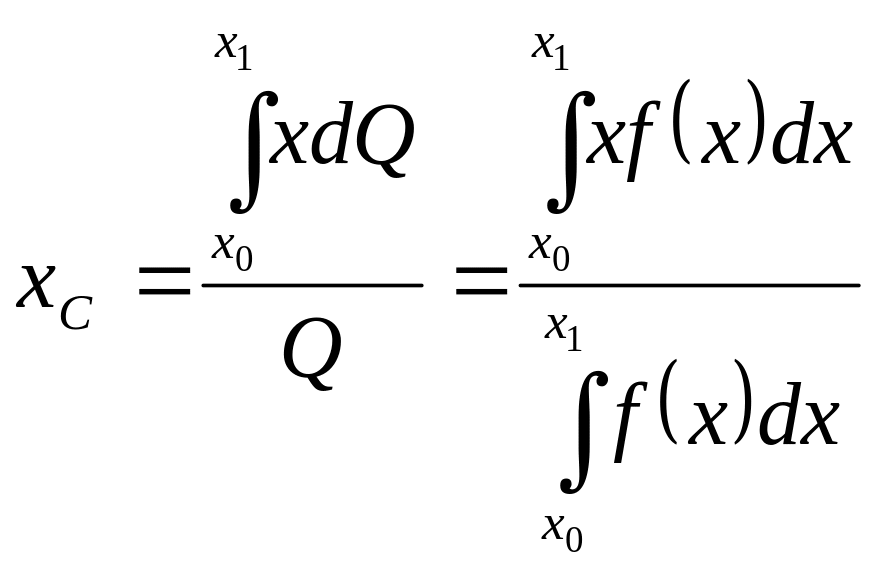 (4.43)

Рис. 4.25

Используя эти зависимости, легко показать, что равно­действующая равномерно распределенной нагрузки (рис. 4.26) равна произведению интенсивности q на дли­ну участка приложения нагрузки, т. е. Q = ql, а точка ее приложения делит этот участок пополам:

.

Если же интенсивность распределенной нагрузки меняется по линейному закону (рис. 4.27), то есть эпюра имеет вид треугольника, то равнодействующая равна

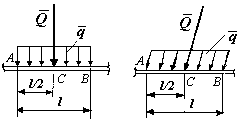
Pис. 4.26

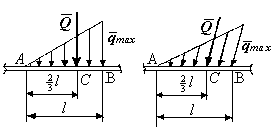
Рис. 4.27

половине произведения максимальной интенсивности на длину участка действия нагрузки Q = q_тахl/2; при этом

.