4.1.5. Классификация связей

Аналитически связи, налагаемые на точку, тело, точ­ки механической системы, выражаются в виде урав­нений связей, в которые в общем случае могут входить координаты точек, их скорости и время. Так, например, если материальная точка движется по некоторой непод­вижной поверхности, то связью является эта поверхность. Координаты точки в каждый момент времени должны удовлетворять уравнению поверхности

(а)

то уравнение этой поверхности и будет уравнением связи, наложенной на точку. Если точка вынуждена двигаться по линии, то уравнениями связи являются уравнения этой линии

(б)

В общем случае уравнение связи, налагаемой на систему точек, записывается в виде

. (в)

В зависимости от вида данной функции связи делят­ся так:

1) геометрические и дифференциальные,

2) стационарные и нестационарные,

3) голономные и неголономные,

4) удерживающие и неудерживающие.

К геометрическим относятся связи, в уравнения кото­рых входят только координаты точек (а, б) системы и, может быть, время. Например, уравнение связи в случае мате­матического маятника постоянной длины с подвесом в начале координат имеет вид , или , то есть связь является геометрической.

Дифференциальными называются связи, уравнения которых кроме координат точек системы содержат, и первые производные от этих координат по времени и, мо­жет быть, время. Примером дифференциальной связи может служить связь, наложенная на колесо, катящееся без скольжения по неподвижной поверхности (рис. 4.10, а). В этом случае скорость центра колеса и его угловая скорость связаны меж­ду собой зависимостью, являю­щейся уравнением этой связи:

, или .

С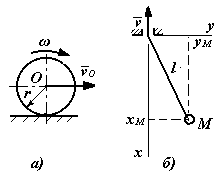 вязи, в уравнения которых время явно не входит, называют­ся стационарными. Разобранные выше связи, наложенные на мате­матический маятник и колесо, являются стационарными. Если же время входит явно в

Рис. 4.10 уравнение связи, то такая связь будет нестационарной.

Пусть нить, на которой подвешен математиче­ский маятник, втягивается в отверстие, совпадающее с точкой подвеса, с постоянной скоростью (рис. 4.10, б). Тогда длина маятника будет переменной: l = lо - vt, где l₀ — первоначальная длина маятника, и уравнение связи принимает вид

, или ^.

Так как время входит в уравнение яв­но, то эта связь нестационарная.

К голономным относятся все геометрические связи, а также те из дифференциальных, которые путем интег­рирования могут быть сведены к геометрическим. Так, например, рассмотренная выше дифференциальная связь, наложенная на колесо, является голономной, так как ее можно проинтегрировать и свести к геометрической. Дей­ствительно,

, то есть

и

,

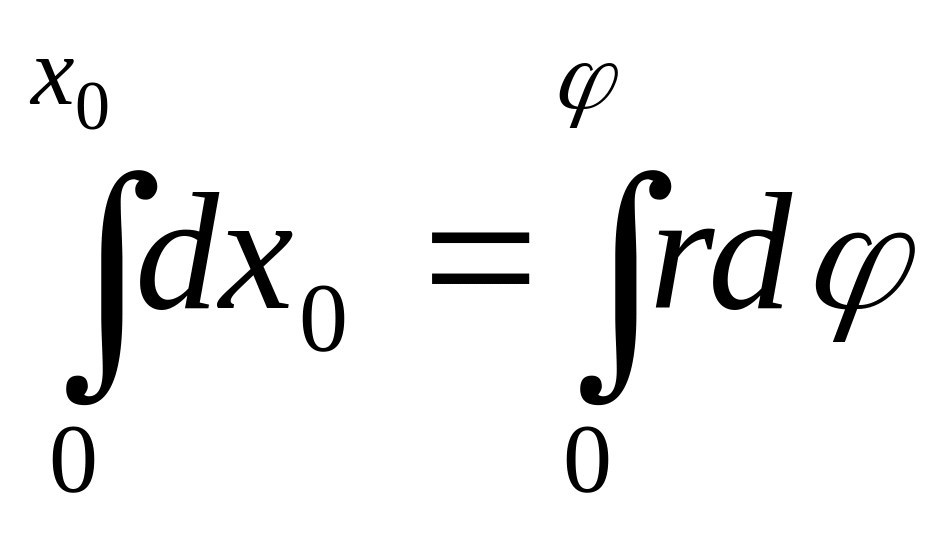откуда , где С - постоянная интегрирования. Дифференциальная связь, уравнение которой не может быть проинтегрировано, называется неголономной.

Если влияние связи не может прекратиться или, ина­че говоря, система не может освободиться от связи, то последняя называется удерживающей. Если же система может покинуть связь, то связь является неудерживаю­щей. Например, жесткий невесомый стержень является удерживающей связью для математического маятника, так как точка М всегда отстоит от точки подвеса О на расстоянии l. Если же математический маятник подвешен на гибкой нерастяжимой нити, то в процессе движения нить может смяться, и расстояние ОМ окажется мень­ше l, т. е. точка М покинет связь. Поэтому в данном слу­чае гибкая нить является неудерживающей связью, и ее уравнение можно записать в виде неравенства . В дальнейшем мы будем, как правило, рассматри­вать механические системы с голономными стационарны­ми удерживающими связями.