5.2. Теорема Вариньона о моменте равнодействующей

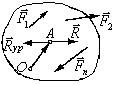
Пусть на твердое тело действует система сил ( ), имеющая равнодействующую, приложен­ную в точке А тела (рис. 5.2). Приложим в точке А уравновешивающую силу _ур равную и противоположно направленную рав­нодействующей, = - Тогда си­стема сил ( , _ур) будет уравновешенной, то есть будет находить­ся в равновесии, и поэтому ее главный момент относительно произвольной точки О равен нулю:

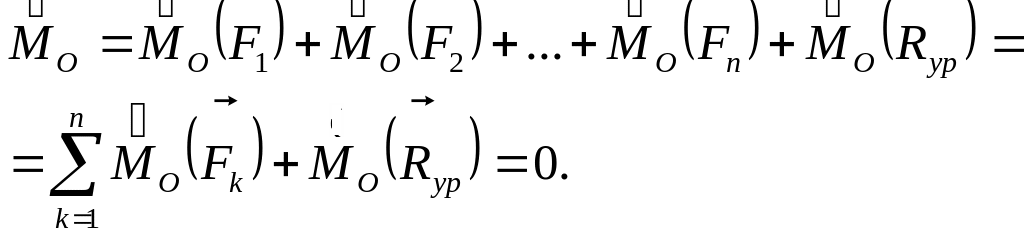
Поскольку _ур= - , то

и, следовательно,

Отсюда получаем формулу, являющуюся математической

Рис. 5.2 записью теоремы Вариньона:

, (5.3)

то есть если система сил, приложенных к твердому телу, имеет равнодействующую, то момент равнодействующей относительно произвольной точки равен сумме моментов всех сил системы относительно той же точки.

Проведем через точку О прямоугольную систему ко­ординат Oxyz и спроектируем на ее оси уравнение (5.3). Тем самым мы получим теорему Вариньона в проекциях на оси декартовой системы координат:

,

, (5.4)

,

то есть момент равнодействующей системы сил относитель­но произвольной оси равен сумме моментов всех сил си­стемы относительно той же оси.

Теоремой Вариньона удобно пользоваться при опреде­лении моментов силы как относительно точки, так и относительно оси.

П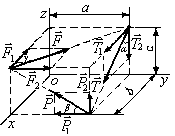 ример. Найти моменты сил , , действующих вдоль диагоналей граней прямоугольного параллелепипеда (рис. 123), относительно осей х, у, z. Размеры параллелепипеда да­ны на рисунке.

Решение. Начнем с определения моментов силы . Для этого разложим ее по правилу параллелограмма на составляющие ₁ и ₂,

Рис. 5.3 парал­лельные осям Ох и Oy. Сила является равнодействующей системы сил ( ₁ , ₂ ). Поэтому по теореме Вариньона

,

так как = 0, поскольку сила ₁ параллельна оси Ох.

Ана­логично

.

Разложив силу на составляющие ₁, ₂ вдоль осей Ох и Оу находим

Предлагаем читателю самостоятельно определить моменты силы .

5.3. Условия равновесия систем сходящихся и параллельных сил

Рассмотренные выше аналитические условия равнове­сия произвольной системы сил, приложенных к твердо­му телу, можно значительно упростить при действии на тело систем сил частного вида, а именно систем сходя­щихся и параллельных сил. Най­дем эти условия.

С истема сил, линии действия которых пересекаются в одной точке, называется системой схо­дящихся сил. При равновесии та­кой системы п сил, действующих на твердое

Рис. 5.4 тело (рис. 5.4), как и в случае произвольной системы, главный вектор системы сил и ее главный момент относительно любой точки должны быть равны нулю:

, .

Введем в рассмотрение радиус-вектор точки А пе­ресечения сил относительно центра О и радиус-вектор точки М_k приложения k-й силы относительно точки А;

Ясно, что . Тогда

, или ( ибо радиус-вектор , коллинеарен вектору силы ).

Из полученного выражения для главного момента следует, что при равенстве нулю главного вектора си­стемы сходящихся сил ее главный момент относительно любого центра тождественно равен нулю. Таким образом, для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы ее главный вектор равнялся нулю:

, (5.5)

и аналитические условия равновесия принимают вид

, , . (5.6)

Определим теперь аналитические условия равновесия системы параллельных сил, то есть системы сил, линии действия которых параллельны. Так как выбор осей координат произволен, направим ось Оz параллельно лини­ям действия сил системы. При таком выборе осей коор­динат проекции всех сил на оси Ох и Oy, а также их моменты относительно оси Oz равны нулю и уравнения

, , .

выполняются тож­дественно; поэтому из шести условий (5.2) равновесия произвольной системы сил в случае параллельных сил остаются только три:

, , . (5.7)

Следовательно, для равновесия системы параллельных сил необходимо и достаточно, чтобы сумма их проекций на ось, параллельную силам, и сумма их моментов отно­сительно двух других осей координат были равны нулю.

Пример 1. Найти усилия S₁ и S₂ в стержнях АВ и АС и на­тяжение Т троса AD (рис. 5.5), если известно, что СВА = BCA = α = 60°, ЕАD = β= 30°, вес груза М равен Р =300 Н, плоскость АВС горизонтальна и в точках А, В и С стержни закреплены шарнирами.

Р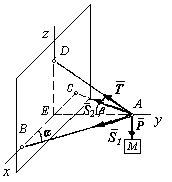 ешение. В качестве тела, равновесие которого мы будем рассматривать в дайной задаче, выберем узел А. На него действуют активная си­ла Р и реакции стержней АВ, АС и троса АD. Реакция троса Т направлена вдоль троса к точке D. Реакции шарнирно закрепленных и нагруженных только в шарнирах прямых стержней на­правлены вдоль осей стержней. Поэтому направим реакции S₁и S₂ от

Рис. 5.5 узла А к точкам В и С, предполагая, что стержни растя­нуты. Таким образом, под действием системы сходящихся сил ( ) узел А находится в равновесии.

Для определения неизвестных реакций проведем оси коорди­нат (рис. 214) и составим уравнения равновесия:

(1) = S₁ cosα - S₂ cos =0,

(2) = - S₁ sinα - S₂ sinα -Т cosβ = 0,

(3) = Т sinβ – P=0.

Из уравнения (1) находим S₁ = S₂. Из уравнения (3) получаем Т = P/sinβ = 600 Н, а из уравнения (2) следует, что S₁= S₂ = - T cosβ/(2sinα) = - 300 Н. Отрицательные значения усилий S₁ и S₂ показывают, что в действительности стержни сжаты и их реакции направлены к узлу А (в данной конструкции это можно было предвидеть). Полученные усилия в стержнях равны между собой, что тоже можно было предвидеть (из соображений симметрии).

П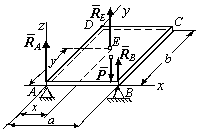 ример 2. Однородная прямоугольная пластина ABCD покоится в горизонтальном положении на трех точечных опорах, две из которых рас­положены в вершинах прямоугольника А и В, а третья — в некоторой точке Е (рис. 5.6), Вес пластины равен Р, а дав­ления на опоры в точках А и В равны Р/4 и Р/5 соот­ветственно. Найти давление R_B на опору в точке Е и ко­ординаты этой точки, если длины сторон пластины равны а и b.

Решение. Рассмотрим равновесие пластины ABCD. На нее действует активная вертикальная сила Р и реакции , ,

Рис. 5.6 гладких точечных опор А, В и Е, направленные нормально плос­кости пластины. Это система параллельных сил, поэтому прове­дем ось А_z вертикально, а оси Ах и Ау совместим со сторонами пластины. Составим уравнения равновесия:

(1) ,

(2) ,

(3) .

Число неизвестных (R_E, х, у) равно числу условий равновесия, поэтому задача статически определима. Решив полученную систе­му уравнений, найдем неизвестные:

R_E = P - R_A - R_B = (11/20) P,

y = Pb/(2R_E) = (10/11)b,

x = a(P - 2R_B)/(2R_E) = (6/11)a.