4.5.2. Кинетический момент системы материальных точек

Кинетическим моментом системы материальных точек относительно центра О называется геометрическая сумма кинетических моментов всех точек системы относительно того же центра:

. (4.90)

Кинетический момент системы приложен к точке О, относительно которой он вычисляется.

Е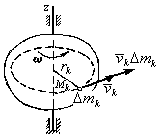 сли спроектировать кинетический момент относительно центра О на оси координат, проходящие через этот центр, то получим проекции кинетическою момента на эти оси (кинетические момен­ты системы относительно осей

Рис. 4.47 координат):

,

,

.

Определим кинетический мо­мент тела относительно его неподвижной оси вращения z (рис. 4.47). Для этого разобьем тело на бесконечно боль­шое количество элементов массой и получим

.

Так как , то . Как известно, входящая в данное выражение сумма рав­на моменту инерции тела относительно оси z: . Тогда окончательно

. (4.91)

Следовательно, кинетический момент твердого тела отно­сительно оси вращения равен произведению момента инерции тела относительно данной оси на угловую ско­рость тела.

Аналогичным образом найдем кинетический момент плоского материального тела, совершающего плоскопараллельное движение, относительно неподвижного центра О, лежащего в плоскости движения те­ла. Разобьем тело на бесконечно большое число элементов массой , каждый из которых можно счи­тать материальной точкой (рис. 4.48). Скорость любой точки тела определяется равенством:

,

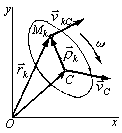где — скорость центра масс тел, и — скорость и радиус-вектор k-й точки тела относительно центра масс, ω — угловая скорость тела.

Так как (рис. 4.48),

Рис. 4.48 то искомый кинетический момент будет равен

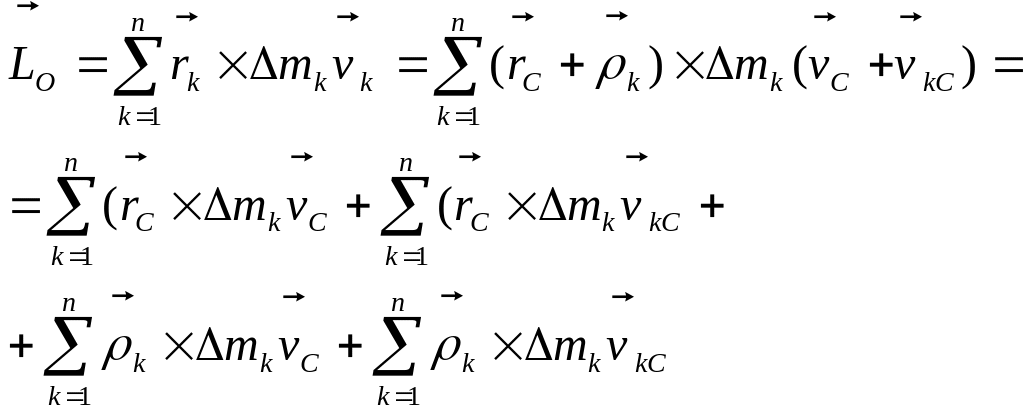Преобразуем каждое из четырех полученных слагаемых:

,

где — масса тела, — количество движения тела, то есть первое слагаемое определяется движением цент­ра масс тела; второе и третье слагаемые равны нулю:

,

Поскольку , что следует из определения цент­ра масс. Так как , то модуль последнего слагаемо­го равен

где J_zC — момент инерции тела относительно оси, перпен­дикулярной плоскости его движения и проходящей через центр масс, то есть это слагаемое (обозначим его ) опре­деляется вращением фигуры вокруг центра масс. Тогда

. (4.92)

Полученное выражение свидетельствует о том, что ки­нетический момент в рассматриваемом примере зависит как от движения центра масс тела, так и от его враща­тельного движения по отношению к центру масс. Этот результат является частным случаем более общей тео­ремы, которую мы сформулируем без доказательства:

кинетический момент механической системы относитель­но неподвижного центра равен геометрической сумме момента относительно этого центра количества движе­ния системы, условно приложенного в центре масс, и кинетического момента системы относительно центра масс в ее относительном движении по отношению к цент­ру масс.

4.5.3. Теорема об изменении кинетического момента системы материальных точек

Запишем для механической системы, состоящей из п материальных точек, дифференциальные уравнения дви­жения в векторной форме (4.30):

, k = l,2,...,n,

где и — соответственно равнодействующие приложенных к k-й точке внешних и внутренних сил. Умно­жим левые и правые части этих равенств слева векторно на радиус-вектор каждой точки относительно неподвиж­ного центра О:

, k = 1,2, ..., п.

Нетрудно показать, что .

Действительно, так как как векторное произведение коллинеарных векторов. Постоянный множитель т_k можно вне­сти под знак производной, следовательно,

, k =1,2,..., п.

Сложим все эти п уравнений:

.

Операции суммирования и дифференцирования переместимы, и поэтому

,

где - кинетический момент системы относительно неподвижного центра О.

По свойству внутренних сил их главный момент равен нулю, то есть . Кроме того, - сумма моментов внешних сил системы относительно центра О, то есть главный момент внешних сил системы относительно точки О. Поэтому окончатель­ная запись теоремы об изменении кинетического момента системы принимает вид

, (4.93)

То есть производная по времени от кинетического момента системы материальных точек относительно неподвижного центра равна главному моменту внешних сил системы от­носительно того же центра.

Спроектировав это равенство на неподвижные оси пря­моугольной системы координат, получим запись теоремы в проекциях на эти оси:

,

, (4.94)

.

Из формул (4.94) следует, что внутренние силы не влияют на изменение кинетического момента системы. Поэтому применение теоремы для исследования движе­ния механической системы позволяет (в той же степени, что и использование теорем об изменении количества дви­жения и движения центра масс системы) исключить из рассмотрения внутренние силы.

Из уравнения (4.93), в частности, следует, что если главный момент внешних сил относительно какого-нибудь неподвижного центра равен нулю, то кинетический мо­мент относительно этого центра остается постоянным, то есть если

то = const. (4.95)

Если же сумма моментов внешних сил системы относи­тельно какой-либо неподвижной оси равна нулю, то соот­ветствующая проекция кинетического момента остается постоянной, то есть если

, то L_x = const. (4.96)

Утверждения (4.95) и (4.96) представляют собой закон сохранения кинетического момента системы.

Закон сохранения кинетического момента часто встре­чается в природе и используется в технических приложе­ниях. Так, выполнение одного из элементов фигурного катания на коньках, вращения на месте с переменной угловой скоростью, основано на этом законе. Действи­тельно, сумма моментов действующих на фигуриста внешних сил (веса и реакции льда) относительно оси вращения равна нулю, и кинетический момент фигури­ста относительно этой оси остается постоянным, то есть J_zω = const. Поэтому для увеличения угловой скорости ω фигурист прижимает руки к туловищу: момент инерции J_z уменьшается, а угловая скорость увеличивается. Если же фигурист хочет замедлить вращение, то он разводит руки в стороны; при этом J_z увеличивается, а ω умень­шается.

Из наиболее интересных технических приложе­ний закона сохранения кинетического момента является использование маховика, установленного в космическом корабле, для изменения угловой ориентации последнего. Предполагается, что космический корабль движется вдали от центров притяжения, и внешние силы на него не действуют. Поэтому центр масс корабля движется по инерции и может рассматриваться как неподвижная точка. Если внешних сил нет, то и главный момент относи­тельно центра масс равен нулю, так что кинетический момент корабля относительно его центра масс и любой его центральной оси остается постоянным, в частности рав­ным нулю. Поэтому для изменения углового положения корпуса корабля начинают вращать маховик в направле­нии, противоположном желательному повороту корпуса. Так как до вращения кинетический момент корабля ра­вен нулю, то он должен оставаться равным нулю и при вращении маховика, а это означает, что корпус будет по­ворачиваться в сторону, противоположную вращению ма­ховика. Когда достигается желаемый угол поворота кор­пуса, маховик останавливается, и вращение корабля пре­кращается.

Если за центр, относительно которого определяется кинетический момент системы, выбрана неинерциально движущаяся точка, то формула (4.92) значительно услож­няется. Однако если этой подвижной точкой является центр масс системы, то формула остается внешне без изменения:

, (4.97)

где — кинетический момент системы в ее движении относительно поступательно движущейся системе коорди­нат, имеющей начало в центре масс системы.