4.2.2. Движение несвободной материальной точки

Рассмотрим материальную точку М, движущуюся под действием задаваемой силы по некоторой поверхности, являющейся для точки связью (рис. 4.14). Пусть уравнение этой поверхности имеет вид: f(x, y, z)=0.

Рассмотрим случай, когда эта поверхность идеально гладкая. В этом случае реакция связи направлена по нормали к поверхности и называется нормальной реакцией. Согласно принципу освобождаемости от связи отбросим связь, заменив ее действие реакцией . Тогда для несвободной материальной точки можно написать основное уравнение динамики:

. (4.15)

С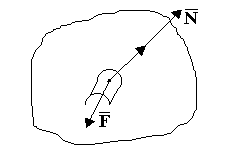 проектировав векторы обеих частей этого равенства на декартовы оси координат, получим дифференциаль-ные уравнения движения материальной точки М

, (4.16)

где Х, У, Z – проекции силы на оси координат, а проекции нормальной реакции N_x, N_y, N_z –

Рис. 4.14 на те же оси, то есть

(4.17)

Косинусы углов, образованных направлением нормальной реакции с осями координат, можно определить по формулам дифференциальной геометрии как направляющие косинусы внешней нормали к поверхности, имеющей уравнение f(x, y, z)=0.

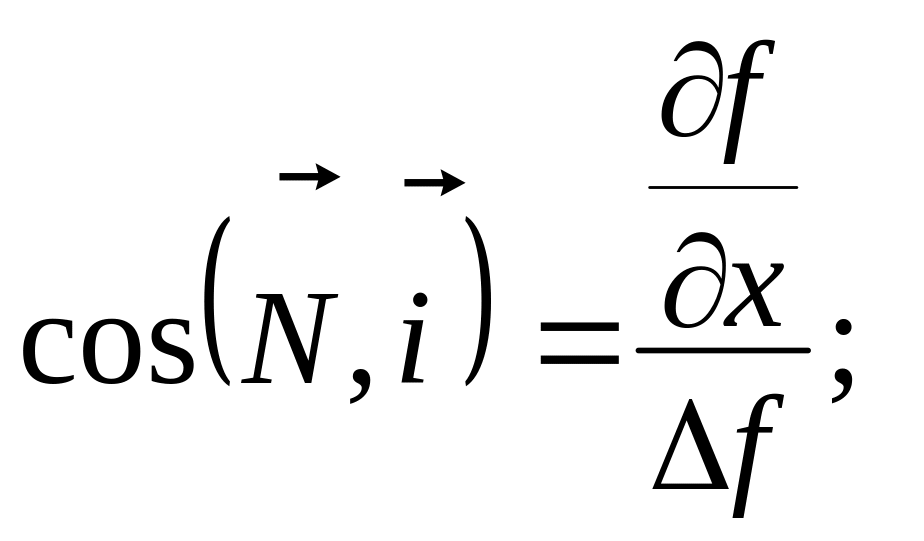
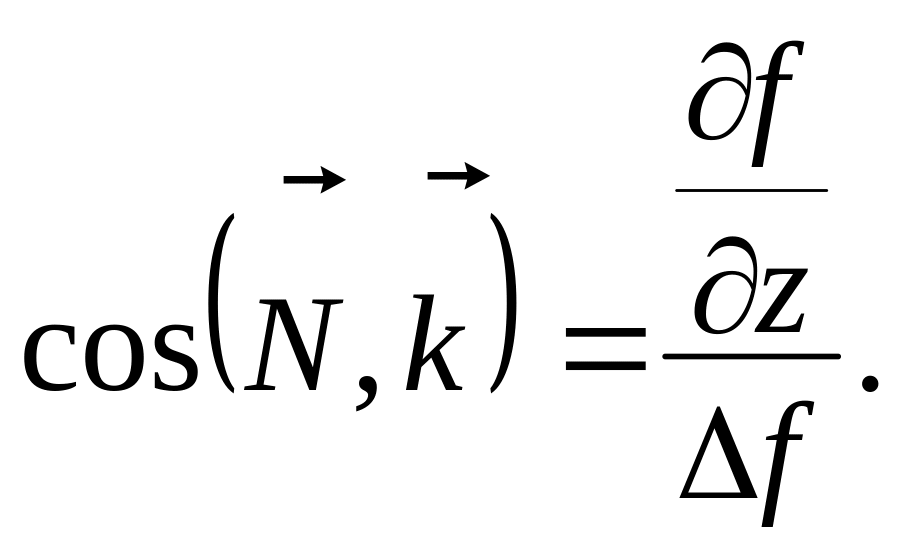(4.18)

где . (4.19)

Если задано уравнение поверхности, то вектор с проекциями функции f, называется градиентом функции f , а N=grad f, здесь  - называется неопределенным множителем Лагранжа.

Подставляя в (4.17) выражения (4.18) получим

; ;

Тогда, подставив найденные значения в (4.16) будем иметь

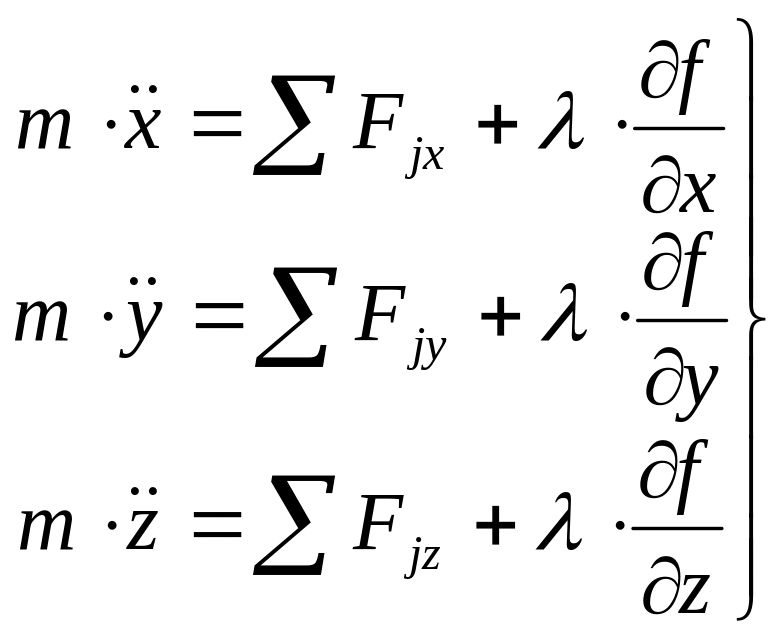(4.20)

Уравнения (4.20) называются дифференциальными уравнениями движения несвободной материальной точки в форме Лагранжа, или уравнениями Лагранжа первого рода.

Из трех дифференциальных уравнений (4.20) и уравнения связи f(x, y, z) = 0 определяют в зависимости от времени четыре неизвестные величины: x, y, z, . Получив координаты точки х, у, z как функции времени, определяют движение точки М. Вычислив множитель Лагранжа  находят из алгебраическое значение нормальной реакции поверхности по формуле

. (4.21)

При движении точки по неподвижной гладкой кривой удобно пользоваться дифференциальными уравнениями в проекциях на естественные оси, так как траектория точки известна:

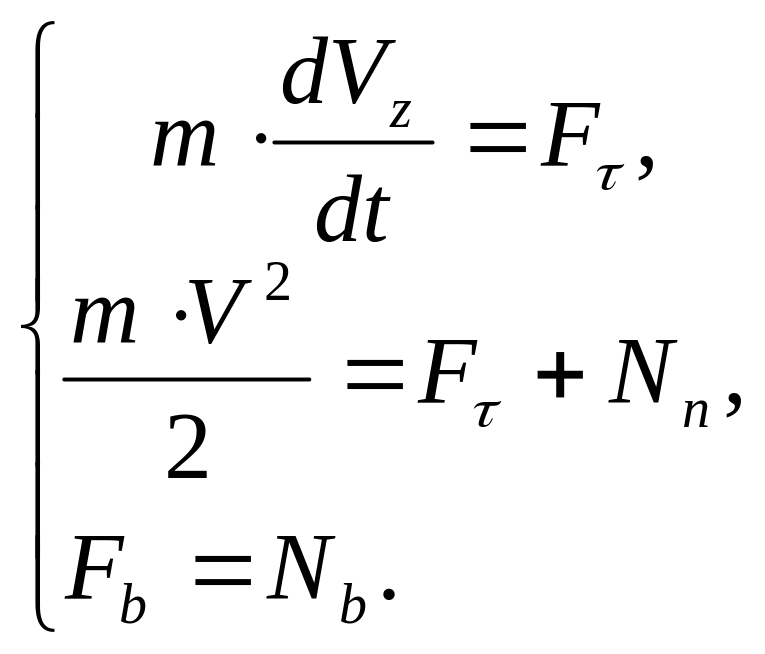(4.22)

а уравнением связи является уравнение кривой.

4.2.3. Дифференциальные уравнения относительного движения материальной точки

Два первых закона классической механики и все полученные на их основе уравнения справедливы для движения материальной точки по отношению к инерциальной системе отсчета.

Изучим движение материальной точки по отношению к инерциальной системе. Пусть система отсчета О₁zhx - инерциальная система (условно неподвижная), а связанная с ней система Oхуz – неинерциальная (подвижная) система отсчета (рис. 4.15). Движение точки М по отношению к системе О₁zhx называется абсолютным, а движение точки по отношению к системе Oхуz называется относительным.

Основное уравнение динамики для абсолютного движения точки М имеет вид:

, (4.23)

где - абсолютное ускорение материальной точки, а -геометрическая сумма приложенных с точке сил.

В разделе «кинематика» установлено, что в случае непоступательного переносного движения абсолютное ускорение точки равно геометрической сумме трех ускорений: переносного , относительного и поворотного (кориолисового) , то есть = + + . Подставив это значение в уравнение (4.23), получим:

т + т + т = .

Из полученного уравнения определим

т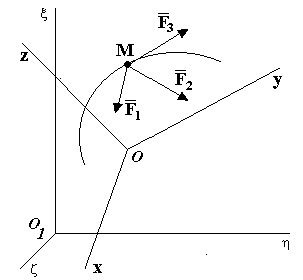 = - т - т (4.24)

Введем два вектора

,

, численно равные произведениям и и направленные противоположно ускорениям . Эти векторы

Рис. 4.15 назовем переносной и кориолисовой силами инерции. Подставив эти векторы в уравнение (4.24) получим:

(4.25)

Уравнение (4.25) представляет собой динамическую теорему Кориолиса - основное уравнение динамики относительного движения материальной точки.

Сопоставляя уравнения (4.23) и (4.25), заключаем, что в случае непоступательного переносного движения, относительное движение материальной точки происходит как абсолютное под действием приложенных к точке сил и условно приложенных к ней переносной и кориолисовой сил инерции.

Рассмотрим частные случаи относительного движения материальной точки, соответствующие различным видам переносного движения.

1. Подвижная система отсчета движется поступательно, тогда w_е=0. Следовательно,

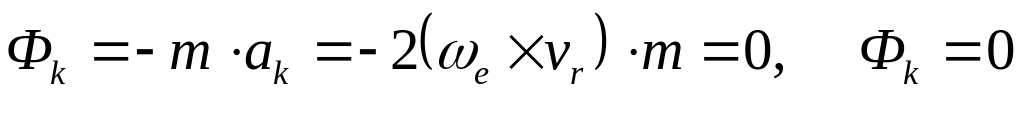2. , тогда

3. Система движется прямолинейно, равномерно, тогда w_е=0, a_е=0, следовательно Ф_к=Ф_е=0, тогда

- это принцип относительности Гилилея-Ньютона. Этот принцип говорит о том, что система координат, движущаяся прямолинейно по отношению к инерциальной системе отсчета сама является инерциальной.

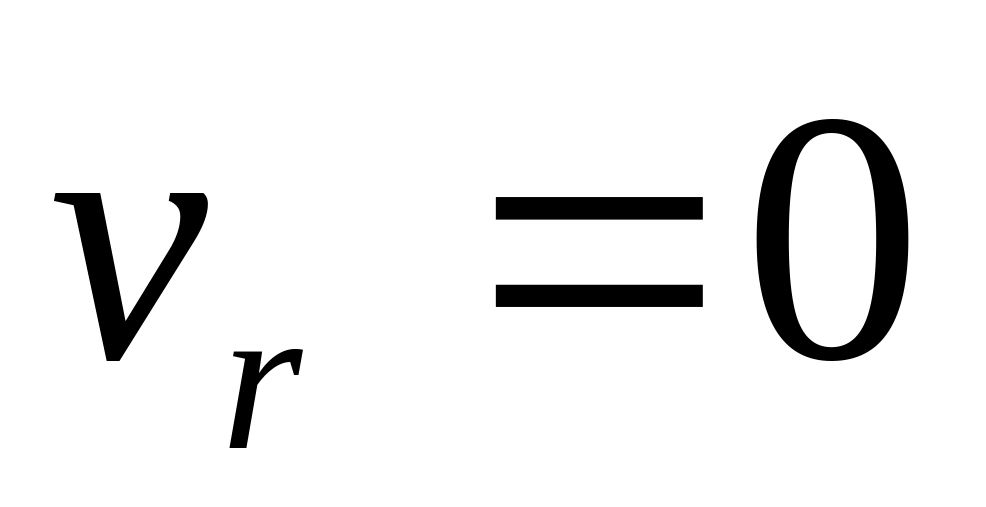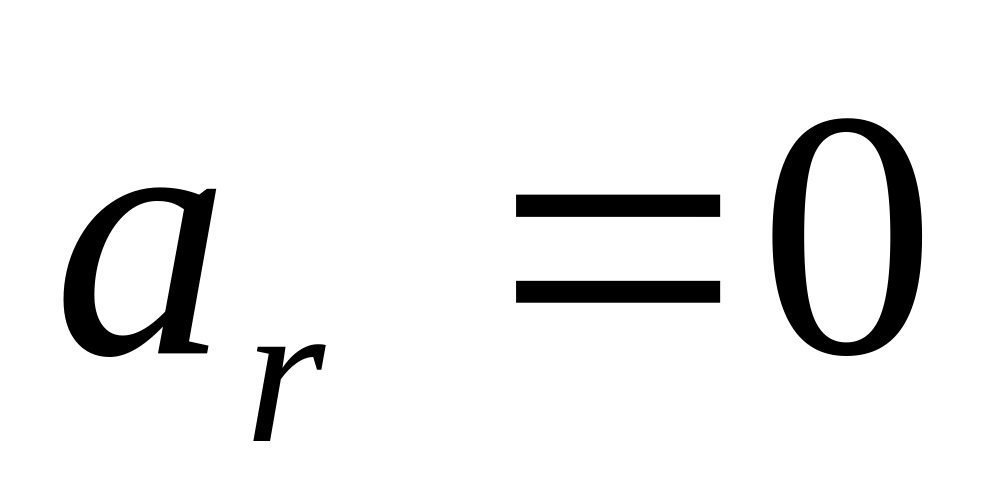4. Если точка в подвижной системе координат не движется, , то есть , Ф_k = 0. Тогда имеем условие относительного равновесия точки

.

Эта формула выражает статическую теорему Кориолиса:

В случае когда материальная точка находится в состоянии относительного покоя, геометрическая сумма приложенных к точке сил и переносной силы равна нулю.