4.6.2. Работа силы

Эффект действия силы на материальное тело зависит не только от времени действия силы, но и от направле­ния силы по отношению к перемещению точки ее приложения, а также от пути, на протяжении которого сила действует на тело. Для описания результата действия силы на материальное тело в зависимости от взаимного рас­положения векторов силы и перемещения и от пути, на котором действует сила, вводится понятие работы силы. Различают элементарную и полную рабо­ту силы.

Элементарная, работа. Пусть матери­альная точка М под действием силы со­вершила элементарное перемещение (рис. 4.51). Тогда элементарной работой dA¹) силы на перемещении называется скалярное произведение силы на элементарное перемещение точки ее приложения:

, (4.104)

где α — угол между направлениями векторов и ).

Рис. 4.51 Так как, = dt, где — скорость точки М, то можно записать еще одно выражение элементарной работы:

dA= dt= F v dt cosα. (4.105)

------------------------------

¹) Из данного обозначения (dA) не следует, что элементарная работа вообще является дифференциалом. Она будет тако­вым только при действии потенциальной силы (см. п.4.6.7).

Из формул элементарной работы следует, что эта величи­на может быть положительной, отрицательной или же равной нулю. Если угол α между векторами и (или ) острый (cosα > 0), то элементарная работа положи­тельна, если угол α тупой (cosα < 0), то элементарная работа отрицательна, а если угол α прямой (cosa = 0), то элементарная работа равна нулю. Кроме последнего случая , элементарная работа равна нулю, если в данный момент F = 0, а также если элементарное пере­мещение равно нулю, т. е. в момент, когда точка М не­подвижна. В частности, силы, приложенные в мгновен­ном центре скоростей тела, не совершают работы.

Обозначим проекции силы на оси декартовой систе­мы координат через F_x, F_y, F_z а проекции элементарного перемещения через dx, dy, dz. Тогда

выражение для элементарной работы (по известному свойству скалярно­го произведения векторов) можно записать в виде

dA= · =F_xdx+F_ydy+F_zdz. (4.106)

В случае, когда к точке М приложена система сил ( ), имеющая равнодействующую ,

элементарная работа равнодействующей на перемещении равна алгебраической сумме элементарных работ сил системы на том же перемещении. Дейст­вительно,

.

Работа силы на конечном перемещении. Пусть мате­риальная точка М под действием силы переместилась из точки А в точку В по кривой l (рис. 4.52). Разобьем кривую l на бесконечное число элементарных отрезков и определим на каждом из них элементарную работу си­лы . Алгебраическая сумма всех этих элементарных работ и будет полной работой силы на конечном переме­щении АВ точки ее приложения вдоль кривой I, т.е. .

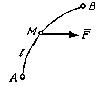Рис. 4.52 Записанная сумма является интегральной и может быть заменена криволинейным интегралом, взятым вдоль кри­вой l на перемещении АВ. Тогда

, (4.107)

или

, (4.108)

где момент времени t = 0 соответствует моменту нахожде­ния точки М в положении А, а момент t — моменту на­хождения точки М в положении В. Последняя запись особенно удобна в том случае, когда сила известна как функция времени. Еще раз необходимо подчеркнуть, что полная работа силы в общем случае зависит от траекто­рии точки ее приложения и лишь в частных случаях, ко­торые мы рассмотрим позднее, зависит только от началь­ного и конечного положений точки приложения.

Единицы измерения элементарной и полной работ одинаковы: это Н·м = Дж (джоуль).

В качестве примеров вычисления полной работы силы найдем работу силы тяже­сти, силы ньютоновского тя­готения и силы упругости.

Работа силы тяжести. Пусть точка М, на которую действует сила тяжести Р = mg, переместилась из положения М₀ с координатами x_0, y_0, z₀ в положение М₁ с координатами x_0, y_0, z₀, (рис. 4.53) (ось Oz направлена вертикально вверх). Опре­делим элементарную и полную работу силы на этом перемещении. Вблизи поверхности Земли силу тяжести можно считать постоянной и направленной по вертикали вниз, поэтому она имеет проекции Р_x=Р_у= 0, P_z = - mg, и ее элементарная

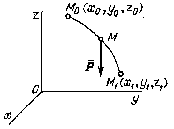Рис. 4.53 работа равна

dA = Р_х dx + Р_у dy + P_zdz = - mg dz.

Полная работа силы на перемещении М₀М₁

,

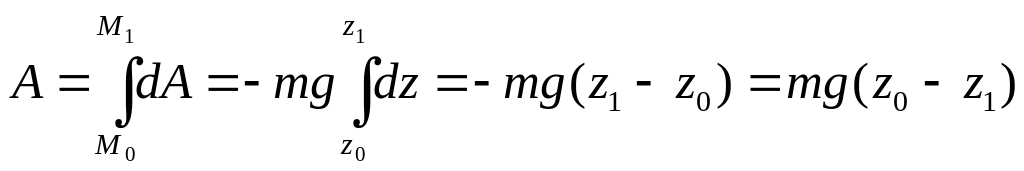
или A = mgh, (4.109)

где h = z₀ - z₁ высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрица­тельна, когда точка поднимается.

Работа силы ньютоновского тя­готения. Пусть на материальную точку М действует сила тяготе­ния, которая притягивает точку к неподвижному центру О и мо­дуль которой равен F = km/r², где т — масса точки М, r — модуль радиуса-вектора точки М относи­тельно центра притяжения, a k —коэффициент пропорциональности (рис. 4.54). В векторной форме силу тяготения можно записать в виде

,

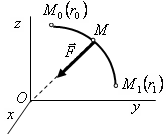где r/ — единичный вектор радиуса-вектора точки М. Элементарная работа этой силы равна

.

Рис. 4.54 Здесь , но скалярное произведение век­тора самого на себя равно просто квадрату его модуля, так что

d( · )/2 = dr²/2 = rdr,

и мы получаем

.

Если точка М переместилась из начального положения М₀(r₀) в конечное положение M₁(r₁), то полная работа силы тяготения на этом перемещении равна А= = 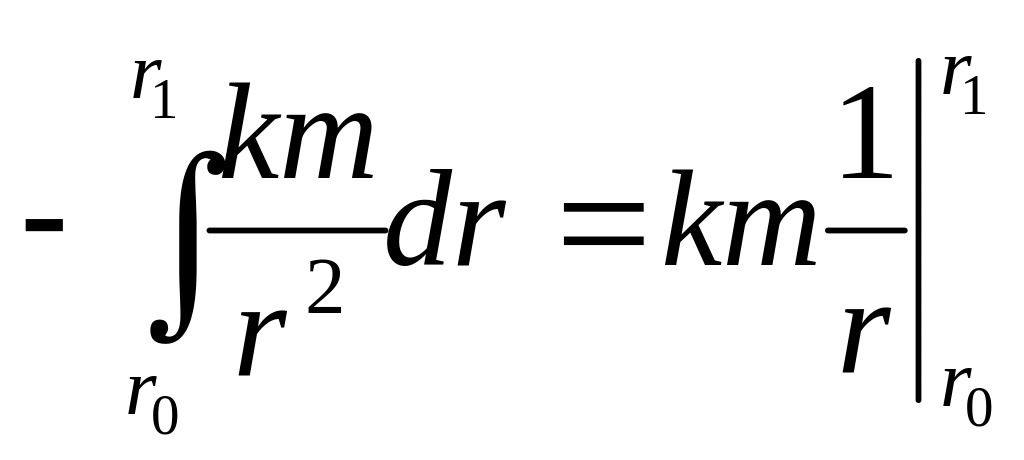, или окончательно

. (4.110)

Работа положительна, если r₀>r₁, то есть если точка при­ближается к центру тяготения.

Работа силы упругости. Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к пру­жине жесткостью с (рис. 4.55). Выберем начало координат в положении, при котором пру­жина не напряжена, и опре­делим работу, которую совер­шит сила упругости пружины при перемещении тела М из положения М₀(х₀) в положе­ние M₁(x₁). Находим проекции силы : F_y = F_z = 0, F_x =.- сх, затем ее элементарную работу:

dA = F_xdx + F_ydy + F_zdz = - cx dx,

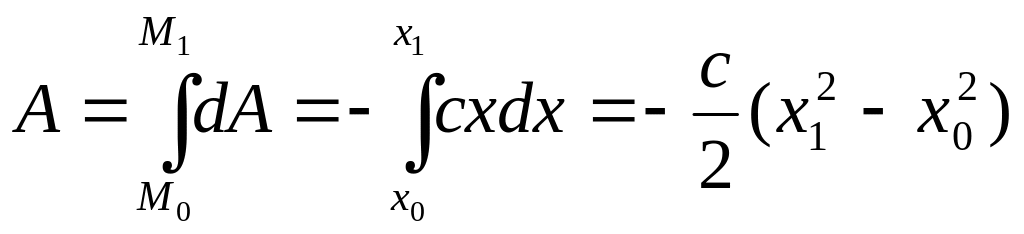и, наконец, полную работу:

и ли окончательно

. (4.111)

При данном выборе начала координат координаты х₀ и х₁ представляют собой начальную

Рис. 4.55 и конечную деформа­ции

пружины, то есть х₀= Δl_нач, х₁=Δl_кон.

Поэтому

А= . (4.112)

Работа силы упругости положительна, если начальная деформация пружины больше конечной, т. е. если точка М приближается к положению, при котором пружина не деформирована.

В разобранных примерах работа силы не зависит от пути, по которому двигалась точка ее приложения. Та­кие силы называются потенциальными.