Решив эту систему, получим

Х_А= Р cos 60° - Q cos 30° = -123 Н,

R_С= (-Q cos 60° AE + P cos 30° AB)/AC = 48,7 Н,

У_А =Q cos 60° + R_С - P sin 60° = 62,2 Н.

Taк как величина Х_A получилась отрицательной, следовательно, действительное направление этой реакции противоположно ее направлению на схеме.

Пример 2. Определить реакции опор А и В балки, на которую действуют две сосредоточенные силы P₁, P₂ и равномерно распределенная нагрузка интенсивностью q (рис. 5.9). Размеры на рисунке даны в метрах, P₁ = 2 кН, Р₂ = 3 кН, q = 0,6 кН/м.

Р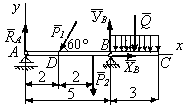 ешение. Рассмотрим равновесие балки. Заменим распределенную нагрузку ее равнодействующей — сосредоточенной си­лой Q, равной

Q = q·ВС = 0,6·3 = 1,8 кН и приложенной в сре­дине отрезка ВС.

Рис. 5.9 Отбросим связи: подвижную шарнирную опо­ру А и неподвижную шарнирную опору В, заменив их реакциями R_А, Х_В, У_В. Балка находится в равновесии под действием плоской системы сил P₁, P₂,, Q, R_А, Х_В, У_В. Проведя оси координат, как это показано на схеме, составим уравнения равновесия этой систе­мы сил:

(1) ; - Р₁ cos60° + Х_В = 0,

(2) ; R_A - Р₁соs30˚- Р₂ + У_В – Q = 0,

(3) ; -Р₁ cos 30^˚·AD – Р₂АЕ +У_В·AB - Q -

- (AB+BC/2)=0.

Решив эту систему, получим

Х_В =P₁ cos 60° = 1 кН,

У_В =P₁ cos 30°AD/AB+Р₂АЕ/АВ+Q2AB+ВС/(2АВ)=5,43 кН,

R_А= P₁ cos 30° + Р₂ + Q - У_b = 1,2 кН.

5.5. Равновесие системы тел. Примеры решения задач

Рассмотренные условия равновесия твердого тела при­менимы и для исследования равновесия механической системы, состоящей из п твердых тел, соединенных меж­ду собой (сочлененных) с помощью различных связей: шарниров, нитей, соприкасающихся поверхностей и т. д. Такие связи называются внутренними в отличие от внеш­них связей, которые связывают рассматриваемую систему с телами, в нее не входящими.

Д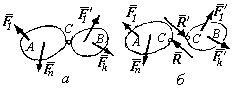 ействительно, если система находится в равновесии, то в равновесии находятся и все тела данной системы. Поэтому мы можем каждое тело освободить от наложенных на него внешних и внутренних связей, заменив их соответствующими реакциями, и рассматривать равнове­сие каждого тела, используя уже знакомые нам условия равновесия. При этом надо иметь ввиду, что внут­ренние силы взаимодействия между телами системы (ак­тивные и реакции внутренних связей) по аксиоме о ра­венстве сил действия и противодействия обязательно рав­ны по модулю и противоположны по направлению. Так, освобождая тело А (рис. 5.10) от внутренней связи в шарнире С и заменяя действие этой связи реакцией , мы должны к телу В, с

Рис. 5.10 которым соединяется тело А шар­ниром С, приложить силу , равную реакции по моду­лю и противоположную ей по направлению.

Из свойства внутренних сил системы вы­текает, что условия равновесия твердого тела справедли­вы и для равновесия системы сочлененных тел.

Действи­тельно, после освобождения каждого тела системы от на­ложенных на него внешних и внутренних связей и заме­ны их соответствующими реакциями, на тело будут дей­ствовать часть внешних сил системы ( , j = 1, 2, ... , m) и часть внутренних сил ( , j =1,2, ..., р), образующих уравновешенную систему сил. Представим главный вектор и главный момент относительно точки О сил, действующих на k-e тело, в виде сумм двух слагаемых:

;

,

где и — сумма внешних сил и сумма внутренних сил системы, действующих на k-e тело; аналогично , . По условиям равновесия

, , k =1,2,…n

Просуммируем эти равенства по всем телам системы:

,

.

Здесь и — главный вектор и главный момент внутренних сил системы, которые по свойству внутренних сил системы равны нулю; , главный вектор и главный момент внешних сил, действующих на систему сочлененных тел.

Таким образом, при равновесии системы сочлененных тел главный вектор и главный момент относительно про­извольной точки внешних сил, действующих на систему, равны нулю:

, 0,

что совпадает с условиями равновесия одного тела. Ана­логичными будут условия равновесия и части системы, состоящей из нескольких тел.

Следовательно, при исследовании равновесия системы сочлененных тел, уравнения равновесия составляются как для нерасчлененной системы, так и для какой-либо ее части и отдельного тела системы. При этом число неза­висимых уравнений равновесия, которое можно составить для системы п сочлененных тел, зависит от типа дейст­вующей на систему нагрузки: при действии произвольной пространственной системы сил число независимых урав­нений равновесия равно 6п, при действии плоской систе­мы сил 3п. Если число этих уравнений равно числу не­известных (реакций внешних и внутренних связей, не­известных внешних сил и геометрических параметров), то все неизвестные определяются из условий равновесия и задача, а также рассматриваемая в ней конструкция, будет статически определимой. В противном случае за­дача является статически неопределимой.

П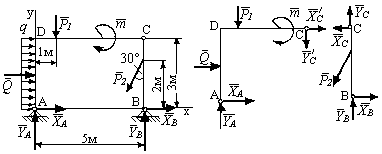 ример 1. Два невесомых стержня ADC и ВС соединены

а) б)

Рис. 5.11

между собой шарниром С и закреплены неподвижными шарнирами в точках А и В (рис. 5.11, а). На систему действуют силы Р₁ = 10 кН, P₂ = 20 кН, равномерно распределенная нагрузка q = 4 кН/м и пара сил с моментом т = 50 кН·м. Размеры даны на схеме. Найти реакции опор А и В, а также усилие в шар­нире С.

Решение. При решении задачи будем рассматривать равно­весие сочлененной системы стержней ADC и ВС. Построим на схе­ме внешние активные силы и моменты, заменив распределенную нагрузку сосредоточенной силой Q =q·3=12 кН, приложенной посредине участка АD. Проведем оси координат, отбросим опоры и заменим их реакциями (рис. 5.11, а). На конструкцию действует плоская система сил, число неизвестных равно шести: и две составляющие реакции шарнира С. Для каждого стержня можно составить три уравнения равновесия, т. е. всего шесть, и поэтому рассматриваемая система статически определима.

Составим три уравнения равновесия нерасчлененной системы:

(1) =Х_А+Х_В+Q-P₂ sin30°=0,

(2) = Y_A+Y_B - P₁ - P₂ cos 30° =0,

(3) = - Y_A·5 - Q·1,5 + P₁·4 - т + Р₂ sin 30°·2= 0.

Из уравнения (3) находим

Y_A = (P₁·4 + P₂ sin 30°·2 - m - Q·1,5)/5 =1,6 кН,

а из уравнения (2) получаем

Y_B = -Y_А +Р₁ + Р₂ cos 30° = 28,9 кН.

В уравнение (1) входят две неизвестные X_А и Х_B, и для их определения надо составить дополнительные уравнения равновесия, расчленяя систему и рассматривая равно­весие какой-либо ее части.

Расчленим систему на составные элементы, то есть отделим стер­жень ADC от стержня ВС (рис. 5.11, б) и приложим к ним в шар­нире С попарно равные и противоположно направленные внут­ренние реакции . Составим уравнения рав­новесия стержня ВС (система сил, приложенных к этому стержню, проще):

(4) = Х_В –Х_C -P₂ sin30°=0,

(5) = Y_C+Y_B - P₂ cos 30°=0,

(6) = X_B·3 - Р₂ sin 30°·1= 0.

Из уравнения (6) наxодим Х_B = Р₂ sin 30°/3 = 3,3 кН, из уравне­ния (5) получаем

Y_C= Р₂ cos 30°- Y_B =11,6 кН,

из уравне­ния (4) находим

Х_C = X_B – Р₂ sin 30° = -6,7 кН,

и, наконец, из уравнения (1) получаем

Х_A =-Х_B - Q + P₂ sin 30° = -5,3 кН.

Величины Y_A, X_A и Х_C отрицательны; следовательно, эти силы в действительности направлены противоположно изображенным на рисунке.

Для решения задачи можно было составлять и другие урав­нения равновесия, например, расчленив систему на элементы ADC и ВС и составив уравнения равновесия каждого элемента.

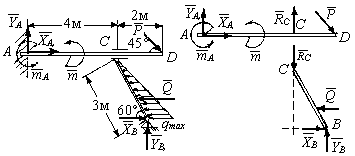Пример 2. Два стержня AD и ВС (рис. 5.12, в) соединены скользящим шарниром (ползуном) С. Опорами системы служат за­делка А я неподвижный шарнир В. На систему действуют сила Р = 20 кН, пара сил, с моментом т = 60 кН·м и распределенная по закону треугольника нагрузка с максимальной интенсивностью q_max=20 кН/м. Размеры даны на схеме. Найти реакции задел­ки A, шарнира В и ползуна С.

а) б)

Рис. 5.12

Решение. Конструкция и действующая на нее система сил являются плоскими. После замены внешних связей реакциями мы получим систему cил, изображенную на рис. 5.12, а. Сила , рав­нодействующая распределенной нагрузки, приложена на расстоя­нии 1 м от точки приложения q_max и равна

Q =½ q_max ·ВС =30 кН.

Если мы будем составлять уравнения равновесия для систе­мы в целом, то, как нетрудно видеть, в каждое из них войдет не менее двух неизвестных реакций, что усложнит вычисления. По­этому расчленим систему и рассмотрим равновесие каждой ее ча­сти в отдельности (рис. 5.12, б). Скользящий шарнир С не допу­скает относительных перемещений стержней только в направле­нии, перпендикулярном стержню AD, так что его реакция направлена перпендикулярно этому стержню. Составим уравнения равновесия стержней, причем для стержня ВС используем вторую форму уравнений равновесия плоской системы сил.

Для стержня AD:

(1) = Х_А + Р cos 45°=0

(2) =Y_А+Rc-P cos 45°=0,

(3) = m_A + т + R_C·4 - Р cos 45°·6 = 0

Для стержня ВС:

(4) =X_B –Q =0

(5) =R_C· 3 cos 60° + Q·1·cos 30° = 0,

(6) = Y_B·3 cos 60°+Q·1·cos 30°=0.

Решая полученную систему шести уравнений, находим т_A= 93,7 кН·м, X_A= -14,1 кН, Y_A=31,4 кН, X_B=30 кН, Yв = -17,3 кН, R_C = -17,3 кН. Реакции Х_A, Y_B, R_C на схеме изо­бражены неверно; в действительности они противоположны пока­занным на рисунке.