Вопросы для повторения

1. Какое перемещение материальной точки называется действи­тельным?

2. Какое перемещение материальной точки называется воз­можным?

3. При каких связях действительное перемещение принадлежит к числу возможных?

4. Зависят ли возможные перемещения от действующих на ме­ханическую систему сил?

5. Что называется возможной работой?

6. Какие связи называются идеальными? Приведите примеры.

7. Условие какого состояния системы определяет принцип воз­можных перемещений?

8. Сформулируйте принцип возможных перемещений.

6. Принцип даламбера

6.1. Принцип Даламбера для материальной точки

Принцип Даламбера устанавливает единый подход к исследованию движения любой механической системы вне зависимости от характера налагаемых на это движе­ние условий. При этом динамическим дифференциальным уравнениям движения придается вид уравнений равно­весия.

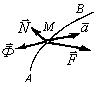
Рассмотрим несвободную материальную точку М, дви­жущуюся по кривой АВ под действием активных сил, равнодействующая которых равна (рис. 6.1). Обозначив через силу реакции, с которой кривая АВ действует на точку М, запишем основное уравнение дина­мики точки

.

Перенесем член в правую часть равенства:

и введем в рассмотрение вектор

Рис. 6.1 , (6.1)

имеющий размерность силы, равный произведению массы точки на ее ускорение и направленный противоположно ускорению точки. Этот вектор называется даламберовой силой инерции, или просто силой инерции мате­риальной точки. Тогда основное уравнение динамики примет вид

. (6.2)

Силы образуют сходящуюся систему сил, а полученное уравнение выражает условие равновесия этой системы, что и составляет принцип Даламбера для мате­риальной точки.

В каждый момент движения материальной точки дей­ствующие на нее активные силы, силы реакций наложен­ных на точку связей и условно приложенная к точке си­ла инерции образуют уравновешенную систему сил.

Прикладывая силу инерции к движущейся точке, мы можем говорить лишь об условном равновесии приложен­ных к ней сил. Однако такая трактовка динамического уравнения движения в некоторых случаях обеспечивает наиболее простое и удобное решение задач динамики (особенно первой), и поэтому принцип Даламбера широ­ко применяется во многих прикладных дисциплинах.

Пример 1. Горизонтальная платформа, на которой лежит груз массой 8 кг, опускается вертикально вниз с ускорением 4,8 м/с². Найти силу давления груза на платформу во время их совместного спуска.

Р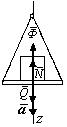 ешение. Рассмотрим движение груза. На него действует сила тяжести и реакция платформы равная по вели­чине и противоположная по направлению силе давления груза на платформу. Поэтому, найдя реакцию мы определим искомую силу. Приложим к грузу (рис. 6.2) силу инерции ,

Рис. 6.2 по модулю равную Ф = mа и направленную противоположно ускорению . Тогда си­стема сил является уравновешенной, и для нее можно за­писать условие равновесия:

,

откуда

N = Q – Ф = m (g - а) = 8(9,8 - 4,8) = 40 Н.

Мы видим, что при ускорении, направленном вниз, сила давления груза на платформу меньше силы тяжести (78,4 Н) груза (если бы ускоре­ние было направлено вверх, то сила давления была бы больше силы тяжести груза).

Пример 2. Груз М массой 0,5 кг, подвешенный на нити длиной 40 см к неподвижной точке О (рис. 6.3), представляет собой конический маятник, который описывает окружность в горизон­тальной плоскости, причем нить составляет с вертикалью угол 60°. Найти скорость v груза и натяжение Т нити.

Решение. Изобразим на схеме си­лу тяжести и реакцию нити , действующие на груз М, и рассмотрим движение груза М по окружности радиусом AM = ОМ sin60°. Ускорение точ­ки состоит из нормальной и касательной составляющих, поэтому представим и силу инерции в виде суммы двух составляющих:

,

равных и .

П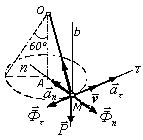 риложим к точке М эти силы, направив их в стороны, проти­воположные соответствующим ускорениям (рис. 6.3). Полученная сходящаяся система сил ( ) уравновешена, и для нее выполняются уравнения равновесия. Составим эти уравнения, предварительно проведя естественные оси координат Мτпb:

∑F_kτ= -Ф_τ = 0,

∑F_kп = Т соs30° - Ф_п = 0,

∑F_kb = Т cos 60° - Р = 0.

Рис. 6.3 Из первого уравнения получим Ф_τ = т dv/dt = 0, или v = const, то есть при движении конического маятника по постоянной окружно­сти его скорость постоянна. Из третьего уравнения находим

Т = mg/cos 60° = 9,8 Н,

и тогда второе уравнение дает

Ф_п = mv²/AM = mg tg 60°,

или

v = (g ·AM ·tg 60°)^½ = (9,8 · 0,2 · 3)^½ = 2,42 м/с.