2.5. Коефіцієнт детермінації : міра «якості підгонки»

Звернемося зараз до розгляду питання якості підгонки лінії регресії до множини даних, тобто дослідимо, наскільки «добре» лінія вибіркової регресії підходить до цих даних. Із рис.1.1 бачимо, що якби всі спостереження знаходилися на лінії регресії, ми отримали б “точну підгонку”, але на практиці це окремий випадок. У загальному ж випадку будуть як позитивні відхилення , так і негативні. Ми прагнемо, щоб ці залишки були наскільки можливо малі. Коефіцієнт детермінації (випадок двох змінних) або (множинна регресія) являє собою сумарну міру якості підгонки лінії регресії до даних спостереження.

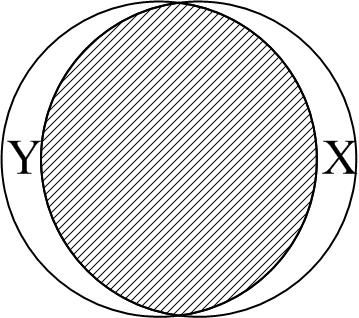
Перш ніж з’ясовувати, як підраховується , розглянемо евристичне пояснення за допомогою графічних діаграм, відомих як діаграма Венна (Venn) (рис. 2.11).

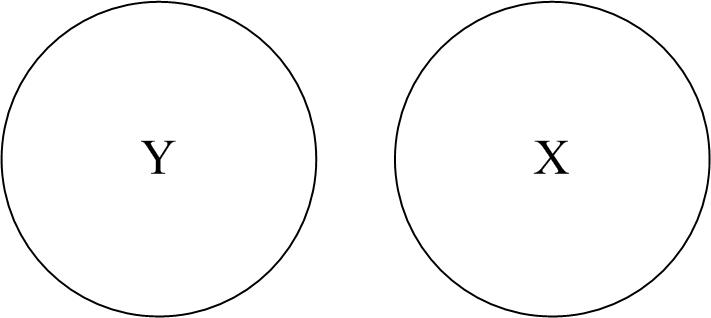
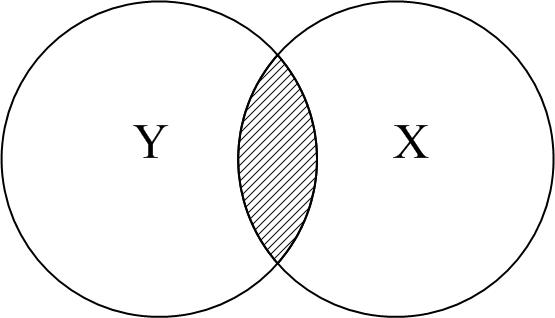
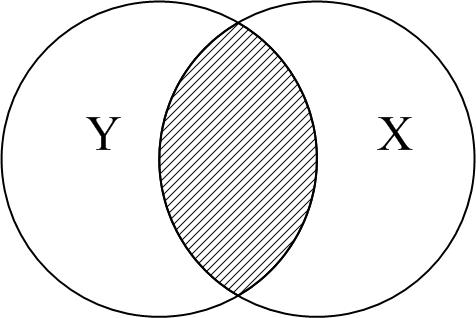
а б в

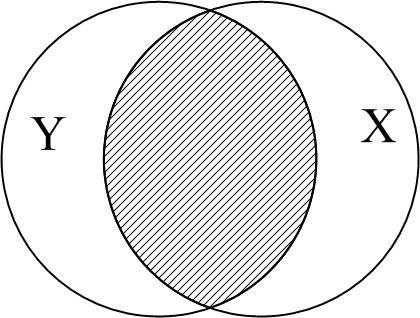
г д е

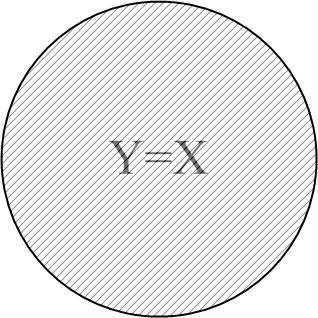
Рис. 2.11. Діаграма для пояснення : а  дорівнює 0; б  близький до 0;

в  близький до 0,5; г  більш ніж 0,5; д  близький до 1;

е  дорівнює 1

На цій діаграмі коло Y зображає дисперсію залежної змінної Y, а коло Х  дисперсію пояснювальної змінної Х. Перетин двох кіл (заштрихована область) являє собою область, у якій дисперсія Y пояснюється дисперсією в Х (скажімо, за регресією МНК). Чим більша область перетину, тим більше дисперсія Y пояснюється за допомогою Х. Коефіцієнт детермінації зображає числову міру області перетину. На рис. 2.9 бачимо, що при русі зліва направо область перекриття збільшується, тобто послідовно зростає частина варіації Y, з’ясована за допомогою Х,  зростає. Коли перекриття немає, , очевидно, дорівнює нулю, а коли відбувається повне перекриття, то , оскільки 100% дисперсії Y пояснюється за допомогою Х. Як незабаром переконаємося лежить між 0 і 1.

Для обчислення коефіцієнта зробимо так. Пригадаємо, що

або у формі відхилень

.

(2.5.1)

Підносячи обидві частини цієї рівності у квадрат і підсумовуючи, отримаємо

,

(2.5.2)

оскільки і .

Різні суми квадратів, що входять у (2.5.2), можуть бути описані таким чином: – загальна дисперсія величини Y відносно середньої величини за вибіркою, що називається загальною сумою квадратів TSS (total sum squares); – дисперсія оціненої величини Y щодо її середнього значення (( ) або з’ясована сума квадратів з рівняння регресії ESS (explained sum squares); – залишкова або нез’ясована дисперсія величини Y щодо лінії регресії або просто залишкова сума квадратів RSS (residual sum squares). Таким чином, з (2.5.2) одержуємо рівність

TSS=ESS+RSS.

(2.5.3)

Вона показує, що загальна варіація спостережуваних величин Y щодо їх середнього значення може бути розбита на дві частини, одна відповідає лінії регресії, а інша  випадковим відхиленням, оскільки не всі спостережувані Y лежать на лінії регресії. На рис. 2.10 це розбиття пояснене геометрично.

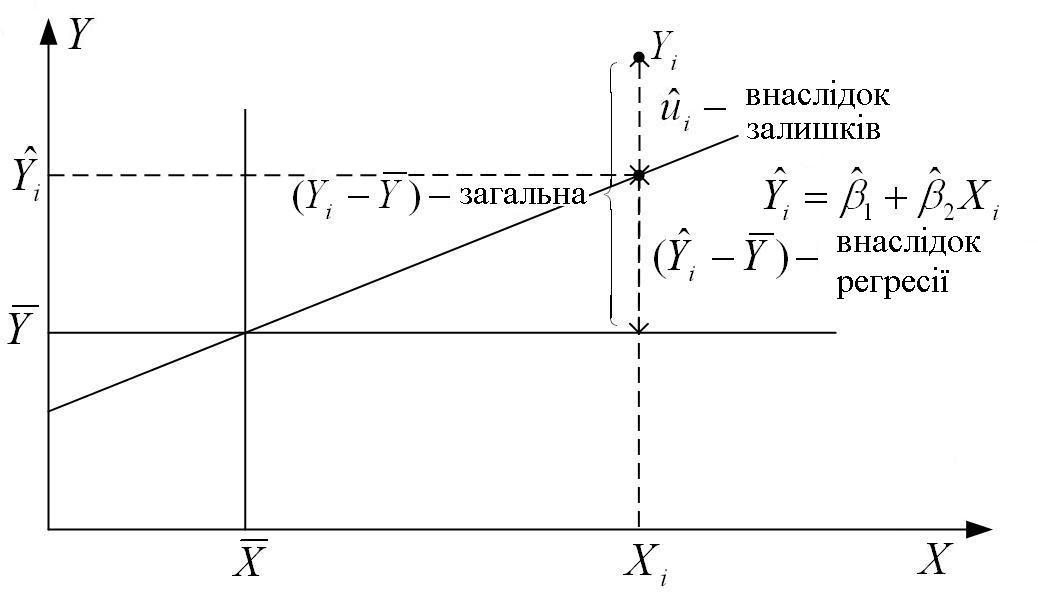
Рис. 2.12. Розбиття варіації на дві компоненти

Розділивши обидві частини (2.5.3) на TSS, одержуємо

.

(2.5.4)

Визначимо тепер коефіцієнт детермінації таким способом:

(2.5.5)

або в альтернативному вигляді

.

(2.5.5а)

Визначена таким чином величина , відома як коефіцієнт детермінації, і є мірою якості підгонки лінії регресії, що широко застосовується.

Відзначимо такі дві властивості :

1. Коефіцієнт не негативний (випливає з виразу (2.5.5)).

2. має межі 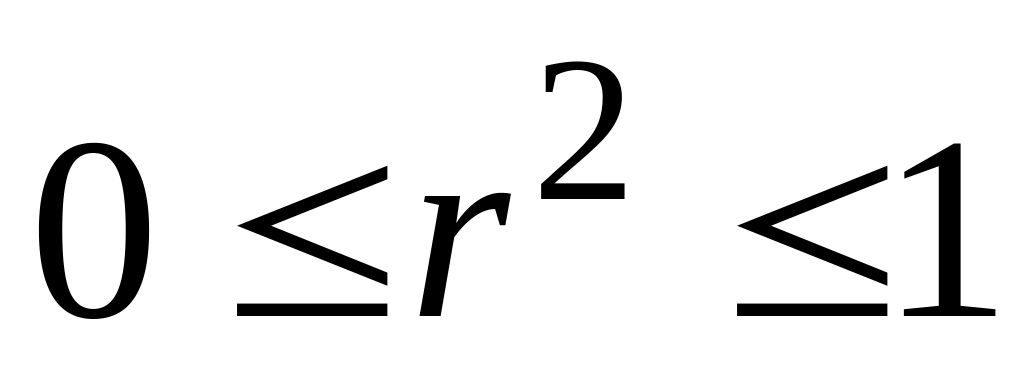. При значенні ми маємо випадок точної підгонки, тобто 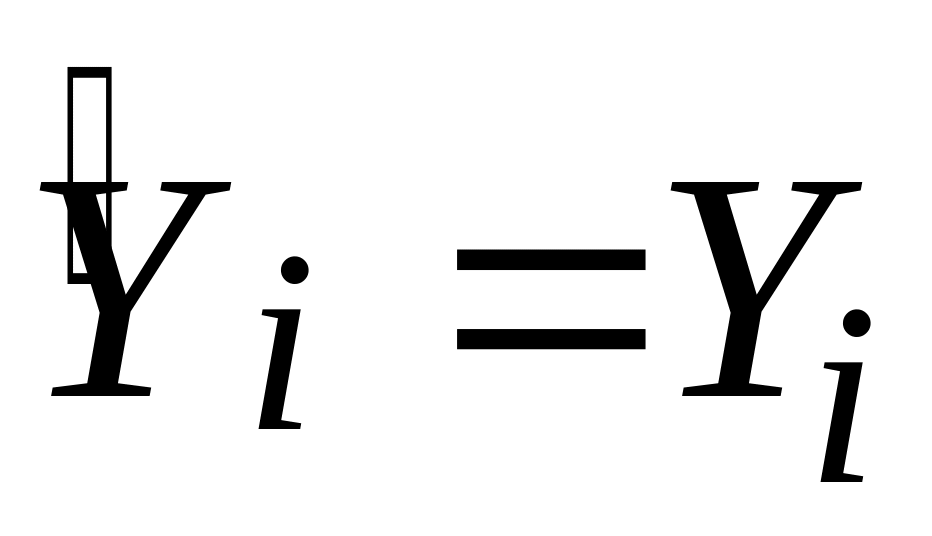для кожного i. Водночас випадок 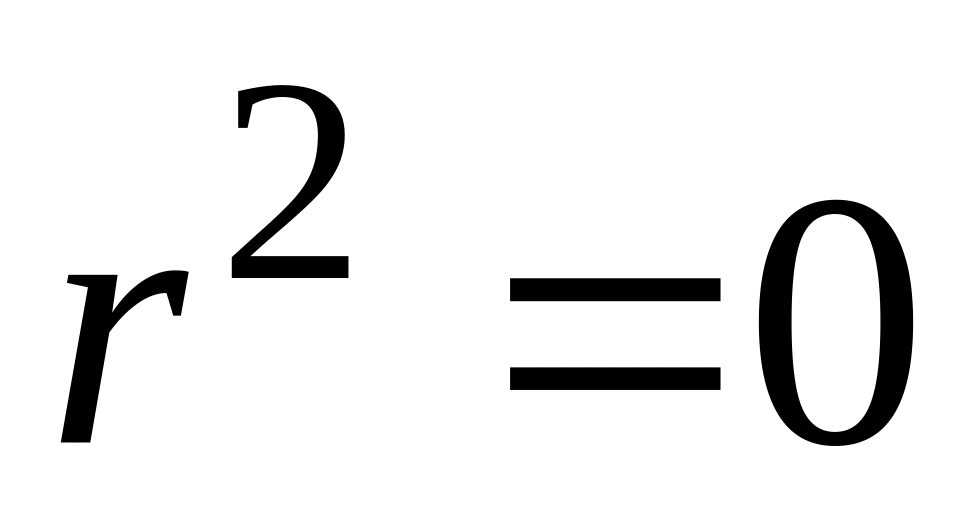означає відсутність зв’язку між регресантом і регресором (тобто 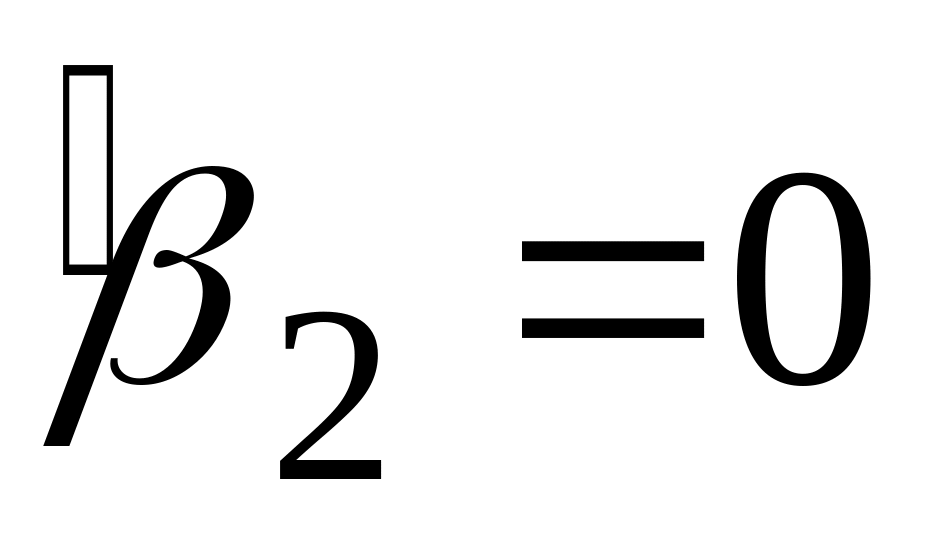, для всіх i). У цьому випадку, як бачимо з рівняння 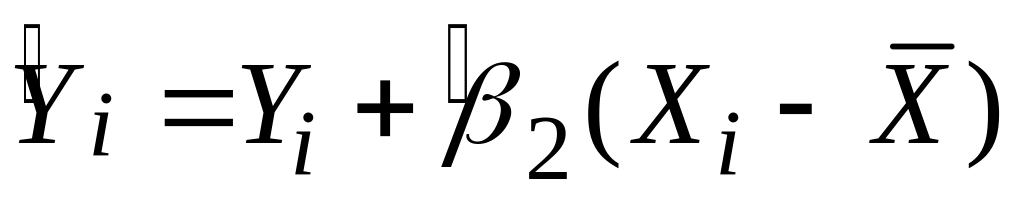, , тобто кращим прогнозом для будь-якої величини Y є її середнє значення. При цьому лінія регресії  паралель осі X.

Хоча можна обчислити безпосередньо за формулами (2.5.5), (2.5.5а), простіше скористатися такими формулами:

.

(2.5.6)

Розділивши чисельник і знаменник (2.5.6) на розмір вибірки N (або N–1, якщо розмір вибірки малий), одержуємо

,

(2.5.7)

де і  вибіркові дисперсії (sample variances) за Y і Х відповідно.

Оскільки , рівняння (2.5.6) можна зобразити у вигляді

.

(2.5.8)

Застосовуючи вирази для , ми можемо подати ESS і RSS таким чином:

,	(2.5.9)
.	(2.5.10)

Отже, ми можемо записати

TSS=ESS+RSS,
.	(2.5.11)

Коефіцієнт кореляції, що являє собою ступінь асоціативності між двома змінними, кількісно близько пов’язаний з , але концептуально вони дуже різні. Коефіцієнт кореляції можна визначити за формулою

	(2.5.12)
або .	(2.5.13)

Визначена таким чином величина має назву коефіцієнта кореляції за вибіркою.

Ось деякі його властивості:

1. Він може бути позитивним або негативним, знак r залежить від знака чисельника (2.5.13), що є мірою коваріації за вибіркою двох змінних.

2. Він лежить між –1 і 1, тобто .

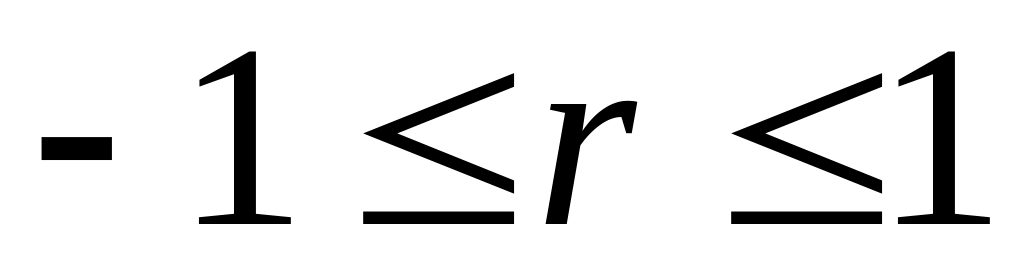3. За своєю природою він симетричний, тобто коефіцієнт кореляції між Х і Y (r_XY) той же, що й між Y і Х (r_YX).

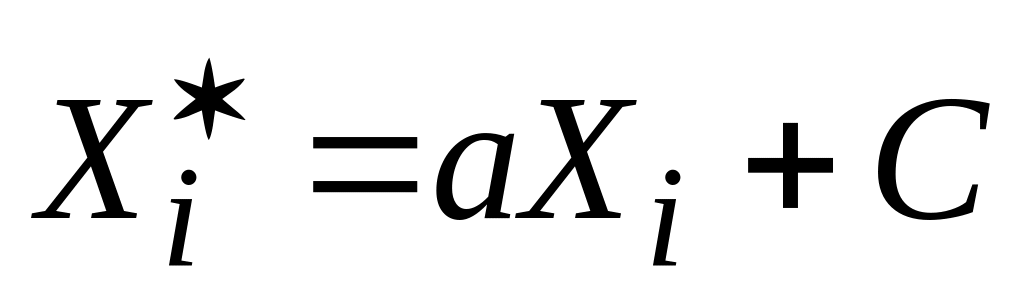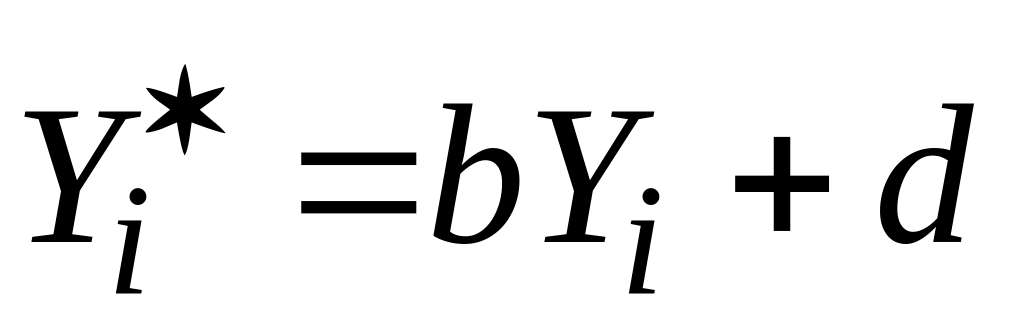4. Він незалежний по відношенню до вибору початку системи координат і масштабу вздовж осей координат, тобто, якщо ми визначимо і , де 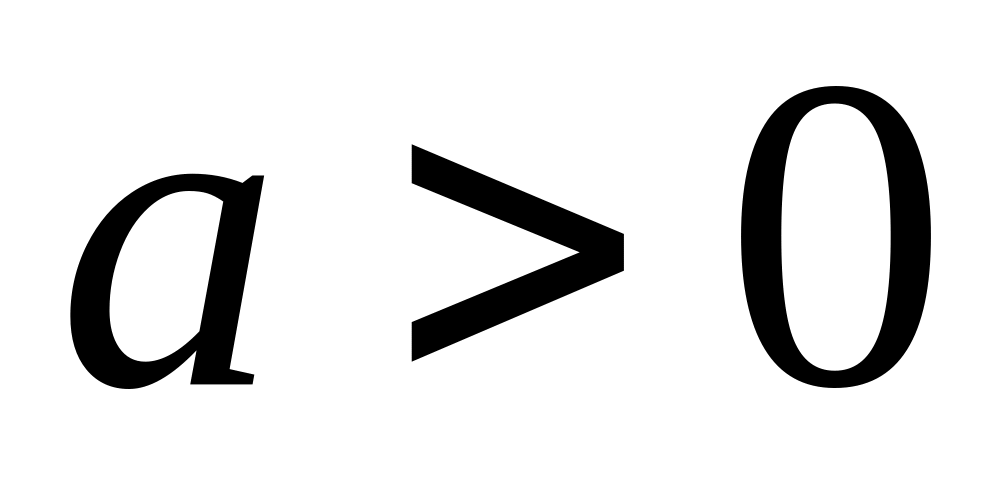, , 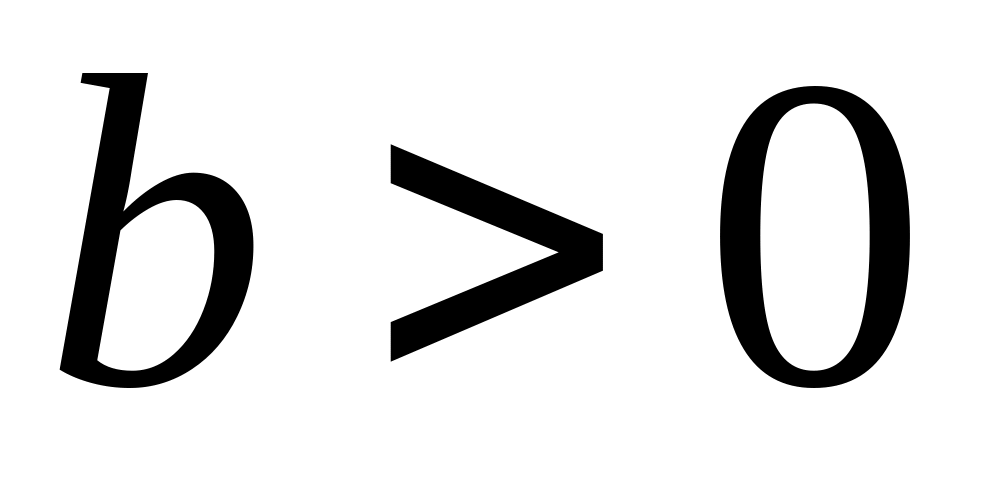а, b і d – константи, то r між Х* і Y* те ж, що й між початковими змінними Х і Y.

5. Якщо Х і Y статистично незалежні, коефіцієнт кореляції між ними дорівнює нулю, але якщо 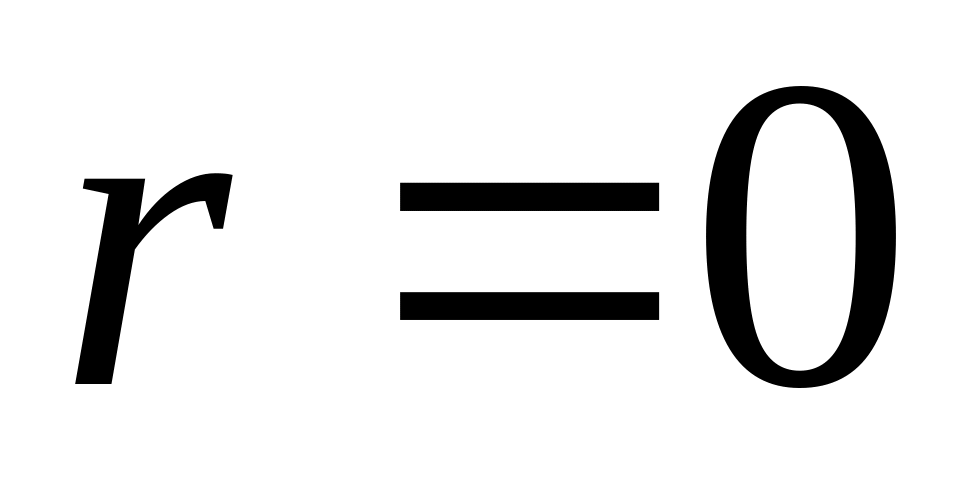, це не означає, що дві змінні незалежні. Іншими словами, нульовий коефіцієнт кореляції не обов’язково означає незалежність (рис. 2.13з).

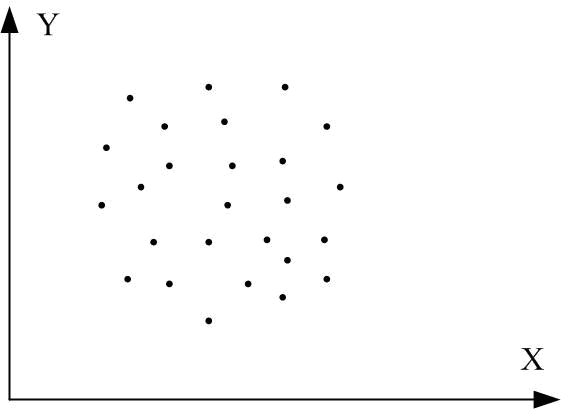
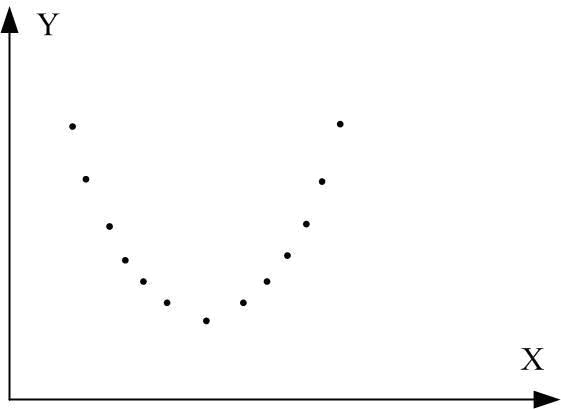
6. Коефіцієнт кореляції є міра тільки лінійної асоціативності або лінійної залежності; він незастосовний для опису нелінійної залежності. Так, на рис. 2.13, з Y=X² є точна залежність, хоча .

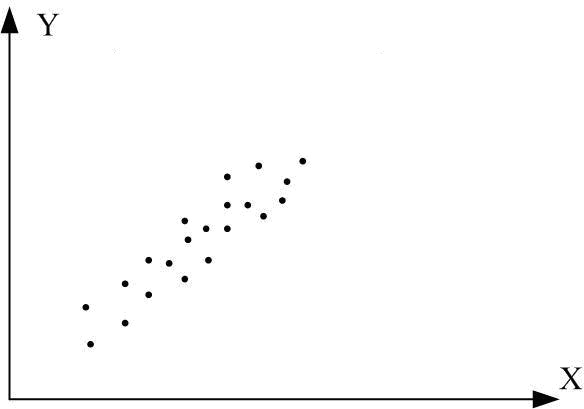
а б в

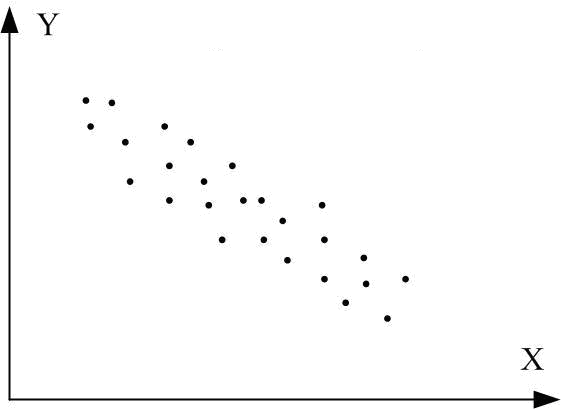
г д е

ж з

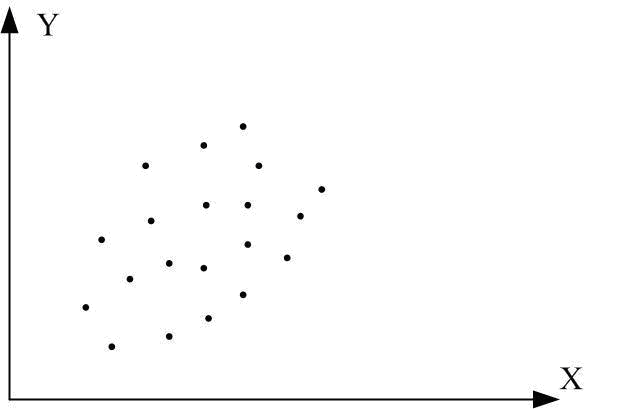
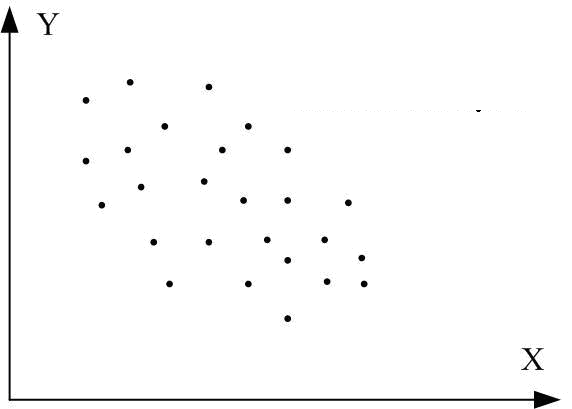
Рис. 2.13. Кореляційний коефіцієнт для різних випадків вибірок:

а  r=1; б  r=-1; в  r близький до 1; г  r близький до –1;

д  r додатній, близький до 0; е  r від’ємний, близький до 0; ж  r=0; з  r=0

7. Хоча r є мірою лінійної асоціативності між двома змінними, це необов’язково означає який-небудь причинно-наслідковий зв’язок, як було відзначено раніше.

У контексті регресії більш інформативний, ніж r, оскільки вказує на частку варіації в залежній змінній, що з’ясовується пояснювальною змінною.

Насамкінець зауважимо, що коефіцієнт детермінації може бути обчислений як квадрат коефіцієнта кореляції між змінними і за такою формулою:

або .
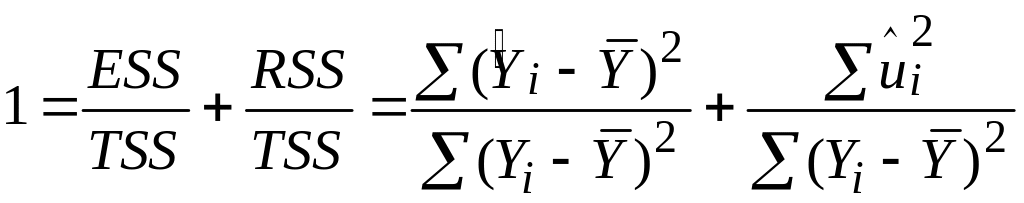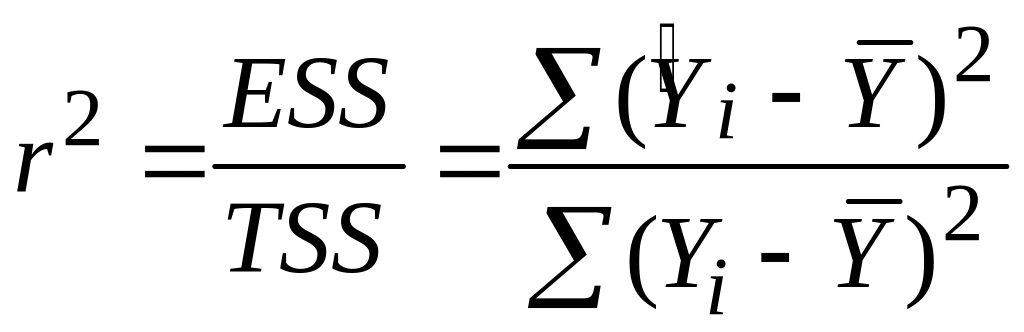
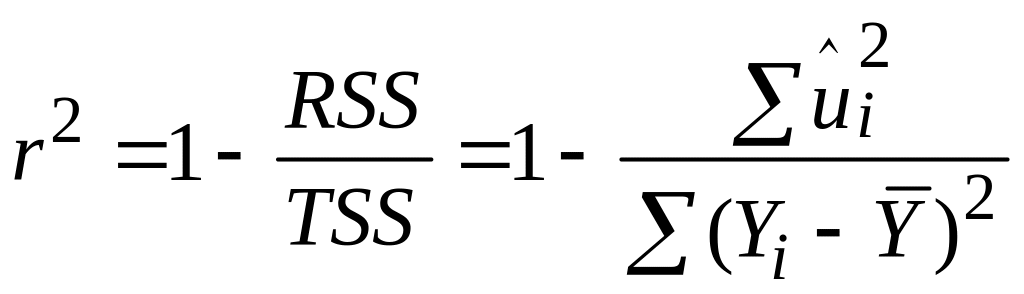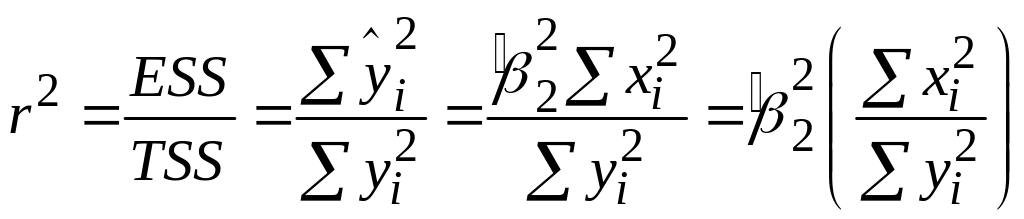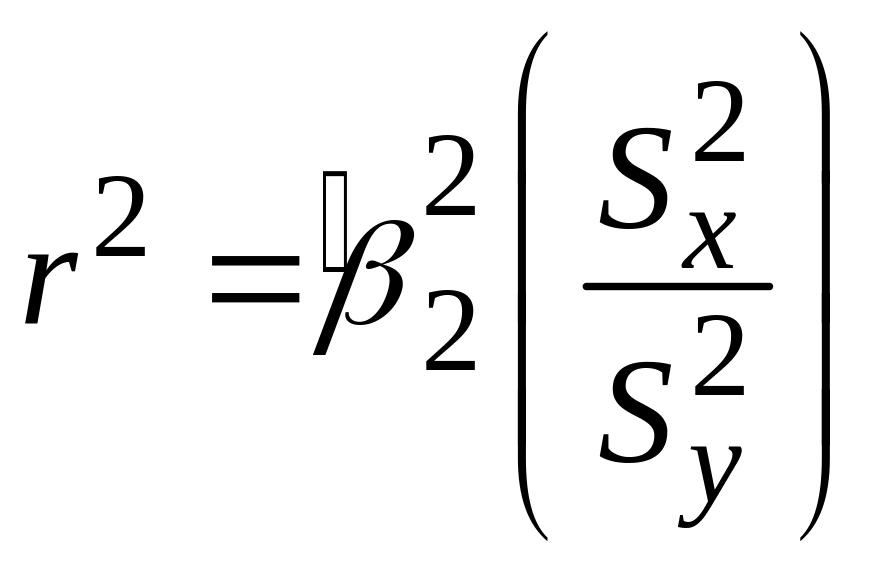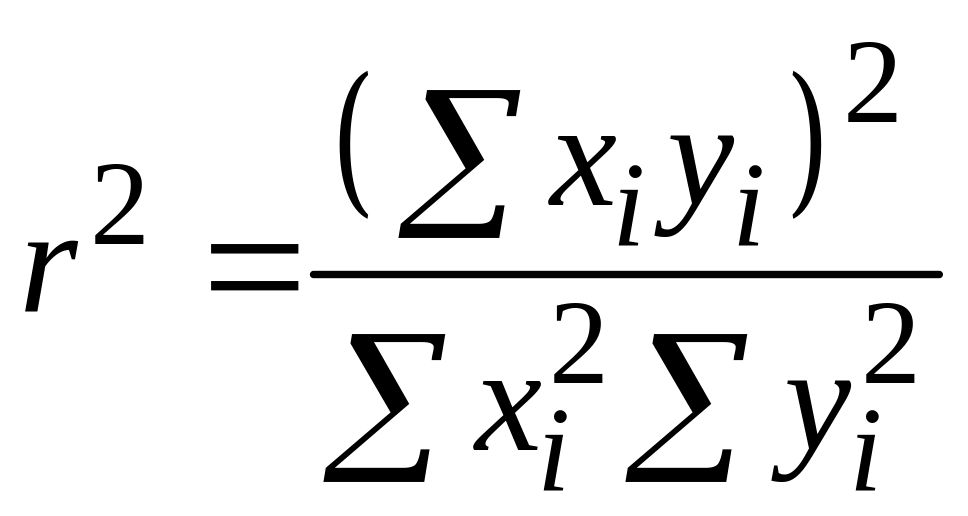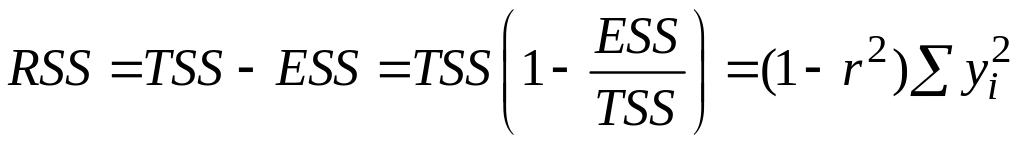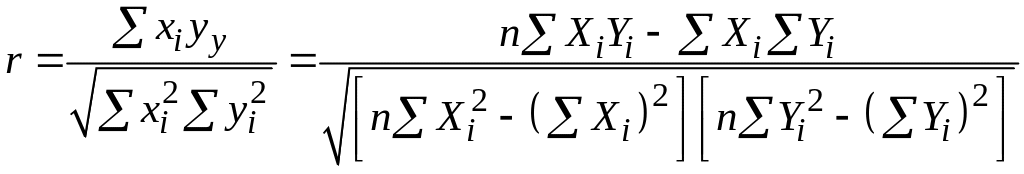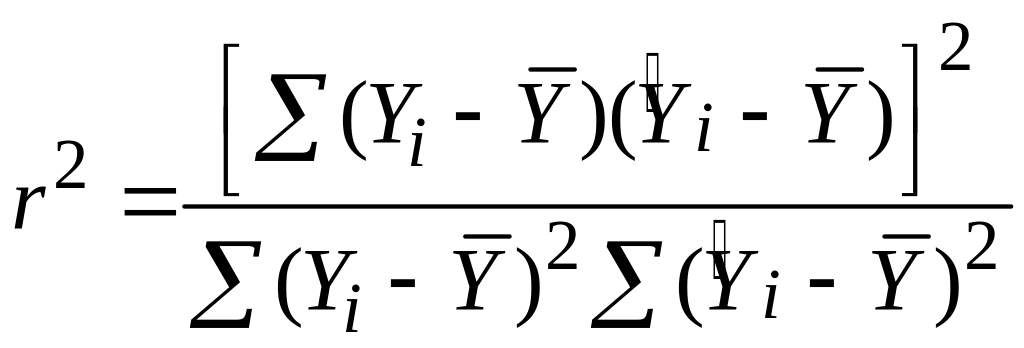
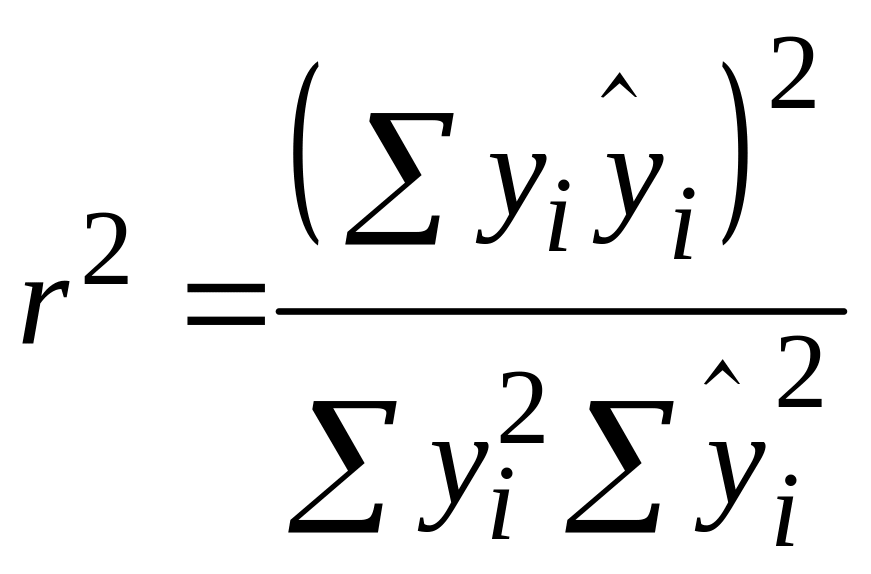