9.7. Загальна перевірка регресії на значущість. Аналіз дисперсії в матричному позначенні

У розд. 8 була розглянута техніка ANOVA загальної перевірки на значущість оціненої регресії, тобто перевірки нульової гіпотези про те, що істинні кутові коефіцієнти одночасно перетворюються в нуль, і оцінювання додаткового внеску пояснювальної змінної. Цю техніку можна поширити на випадок k змінних. Пригадаємо, що механізм полягає в розкладанні TSS на дві складові: ESS і RSS. Матричні вирази для цих трьох сум квадратів уже наведені в (9.3.10) – (9.3.12). Асоційовані з ними кількості степенів вільності відповідно дорівнюють (n–1), (k–1) і (n–k). За аналогією з табл. 8.2 ми можемо скласти табл. 9.2.

Таблиця 9.2

Матричне формулювання anova-таблиці

для лінійної моделі регресії з k змінними.

Джерело дисперсії	SS	DF	MSS
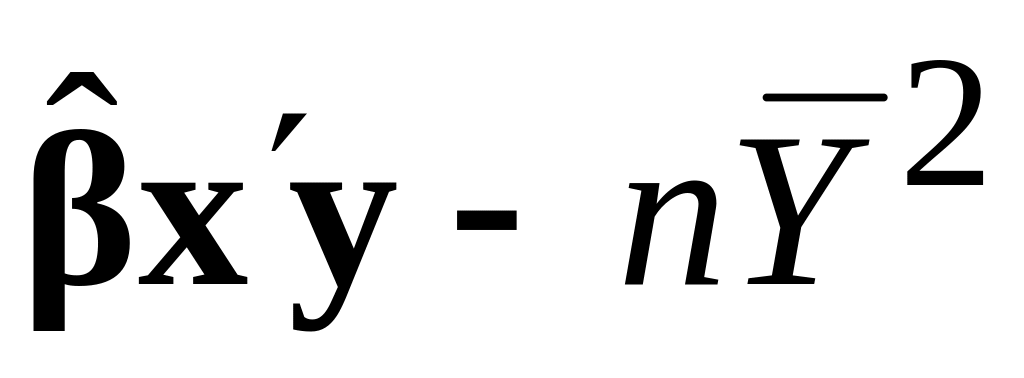
Унаслідок регресії		k–1
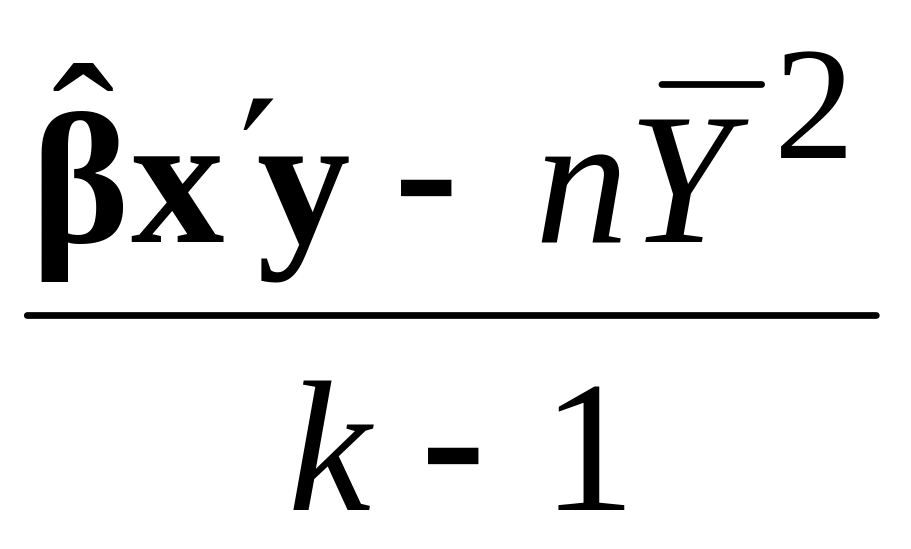
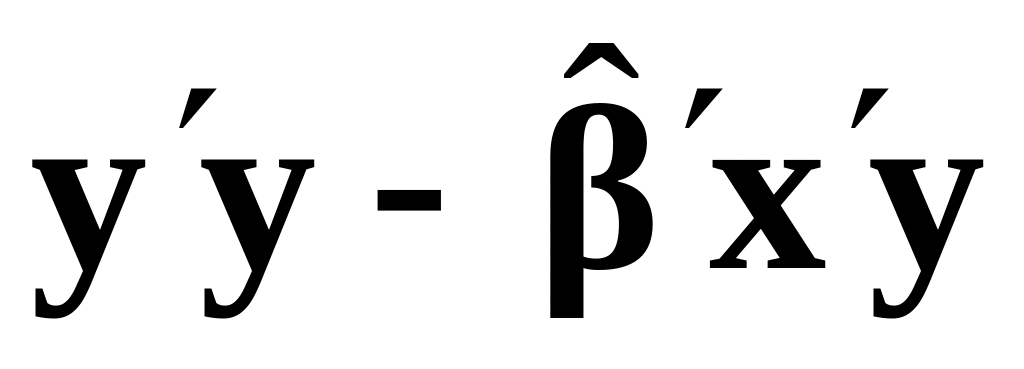
Унаслідок залишків		n–k
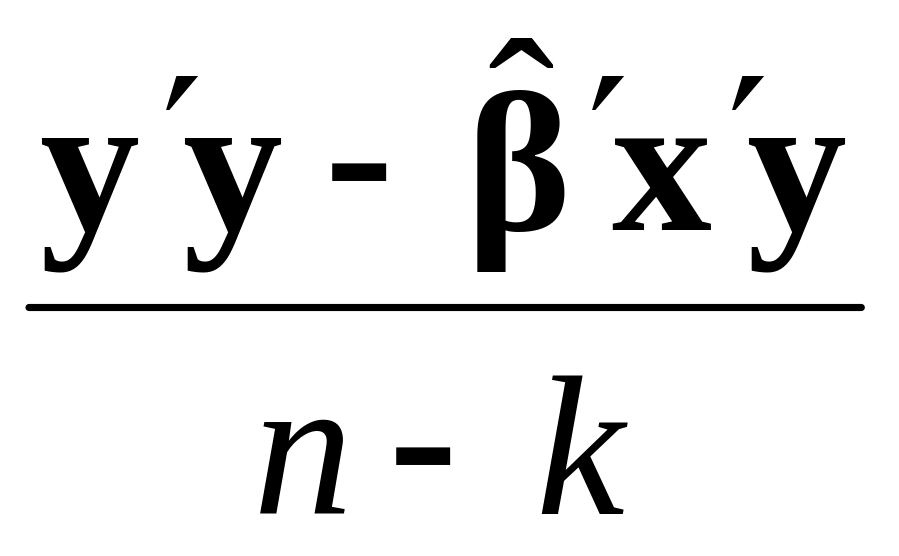
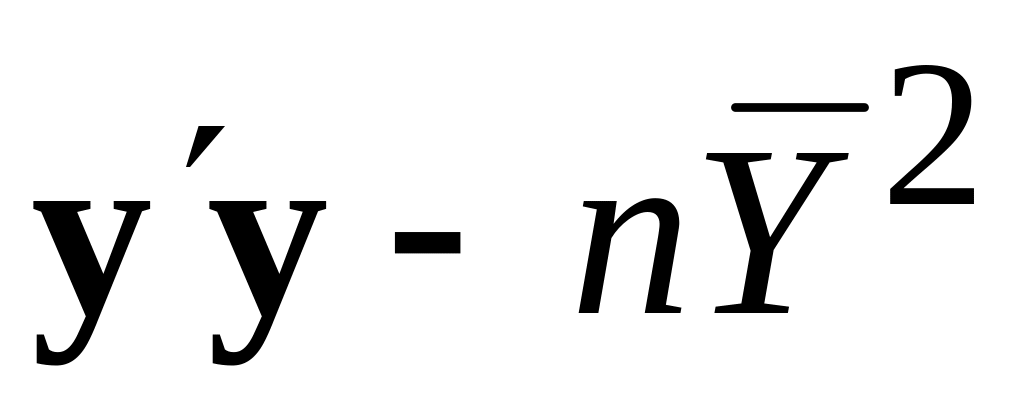
Загальна		n–1

Припускаючи, що збурення розподілені нормально й нульова гіпотеза є , як і в розд. 8, можна показати, що

.

(9.7.1)

розподілено за законом F-розподілу з (k–1) і (n–k) степенями вільності.

У розд. 8 ми бачили, що при зроблених вище припущеннях існує тісний зв’язок між F і R², а саме

.

Отже, табл. 9.2 може бути перетворена до вигляду табл. 9.3.

Таблиця 9.3

ANOVA-таблиця для k змінних в термінах R²

Джерело дисперсії	SS	DF	MSS
Унаслідок регресії		k–1
За залишками		n–k
Загальна		n–1

Однією з переваг табл. 9.3 в порівнянні з табл. 9.2 є те, що весь аналіз може бути виконаний у термінах R²; немає потреби розглядати складова , оскільки він випадає з виразу для F.

9.8. Перевірка лінійних обмежень. Загальний f-тест у матричних позначеннях

У розд. 8 ми описали загальний F-тест для перевірки справедливості лінійних обмежень, що накладаються на один або більше параметрів лінійної регресії з k змінними. Відповідний тест визначається рівнянням (7.4.9). Матричний аналог цього рівняння можна отримати дуже легко. Хай

• – вектор залишків регресії з обмеженнями;

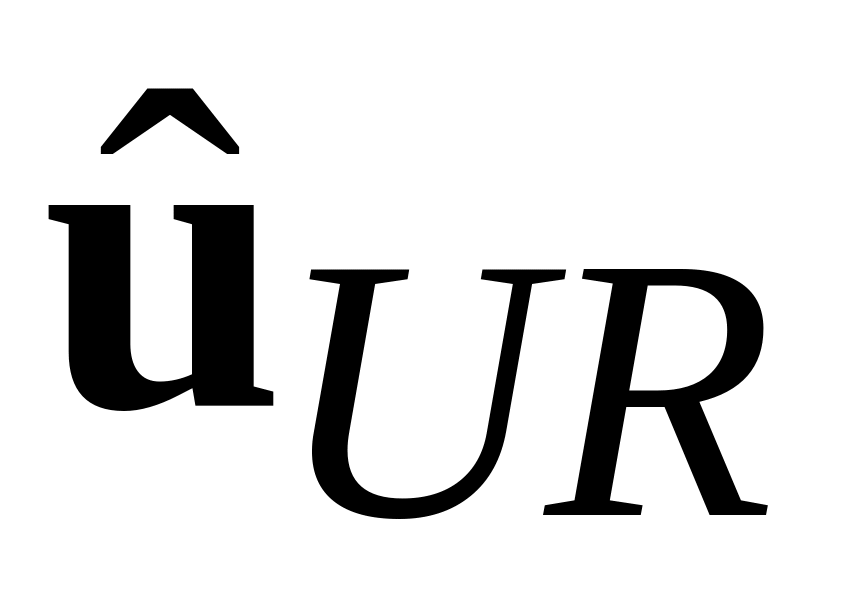• – вектор залишків регресії без обмежень.

Тоді

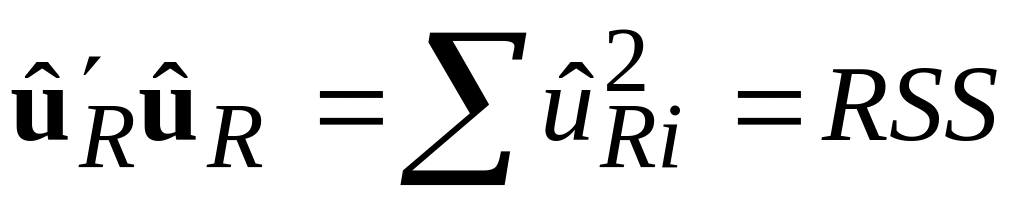• з регресії з обмеженнями;

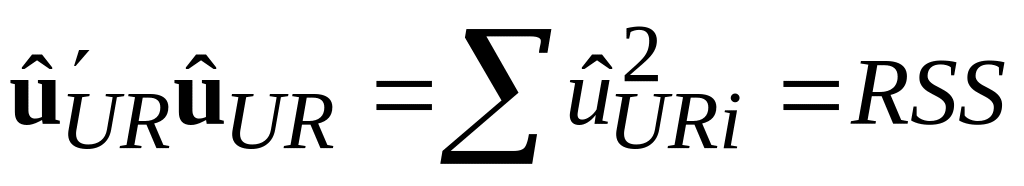• з регресії без урахування обмежень;

• m – кількість лінійних обмежень;

• k– кількість параметрів у регресії без обмежень;

• n – кількість спостережень.

Матричний аналог формули (7.4.9) має вигляд

.

(9.8.1)

У цій формулі F підкоряється закону F-розподілу з (m, n–k) степенями вільності. Як завжди, якщо підрахована величина F більша критичного значення, ми можемо відкинути обмеження на регресію, у протилежному випадку ми їх не відкидаємо.
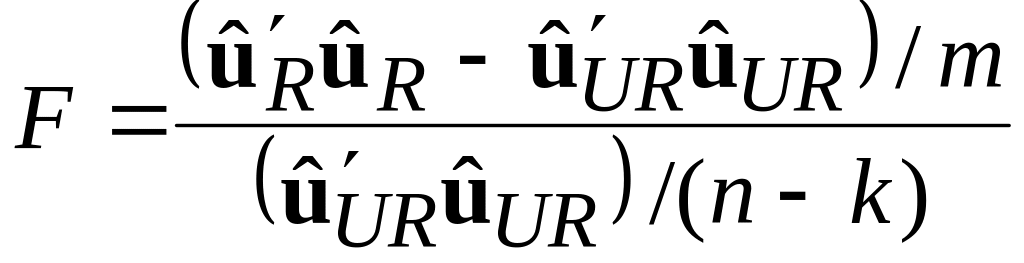