3.9. Застосування регресійного аналізу: проблема прогнозу

На основі вибіркових даних табл. 3.2 нами було отримане таке рівняння вибіркової регресії:

,

(3.9.1)

де – оцінювач істинного , відповідного даному Х. Яка користь може бути отримана з цієї історичної регресії (historical regression)? Рівняння можна застосовувати для прогнозу або передбачення майбутніх споживацьких витрат Y, відповідних деякому даному рівню доходу Х. Можливі такі два види прогнозу:

1. Прогноз умовної середньої величини Y, відповідний вибраному Х, скажімо Х₀, тобто точки на самій лінії регресії популяції.

2. Прогноз індивідуальної величини Y, відповідної Х₀.

Ми називатимемо ці два прогнози середнім прогнозом й індивідуальним прогнозом.

Середній прогноз

Для більшої чіткості припустимо, що Х₀=100 і ми хочемо спрогнозувати E(Y/X₀=100). Зрозуміло, що рівняння історичної регресії (2.6.2) дає оцінку середнього прогнозу таким чином:

,

(3.9.2)

де – оцінка E(Y/X₀). Можна показати, що цей точковий прогноз  краща лінійна незміщена оцінка (best linear unbiased estimator, BLUE).

Оскільки є оцінкою, напевно числове її значення відрізняється від істинного. Різниця між двома цими величинами дасть деяке уявлення про помилку прогнозу. Для отримання цієї помилки нам необхідно знайти розподіл вибірки . , з формули (3.6.1),  нормально розподілена величина із середнім (₁₊₂Х₀) і її дисперсія задається такою формулою:

.

(3.9.3)

Позначимо невідому її незміщеною оцінкою . Тоді змінна

(3.9.4)

розподілена за законом розподілу Ст’юдента з N–2 степенями вільності. Отже, цей закон розподілу можна застосовувати для побудови довірчих інтервалів істинного E(Y₀|X₀) і перевірки гіпотез звичайним способом:

,

(3.9.5)

де отримано з (3.6.2):

.

Для наших даних одержуємо

і .

Отже, 95%-й довірчий інтервал для істинного E(Y₀|X₀)=₁₊₂Х₀ задається формулою

.

(3.9.6)

Таким чином, для Х₀=100 у вибірках, що повторюються, 95 зі 100 інтервалів, подібних (3.6.5), міститимуть істинну середню величину; найкращим точковим оцінювачем буде 75,3645.

Якщо ми отримаємо 95%-ві довірчі інтервали, подібні (3.9.7), для кожного значення Х, наведених у табл. 1.3, ми отримаємо довірчу область (confidence band) для функції регресії популяції, показаної на рис. 3.6.

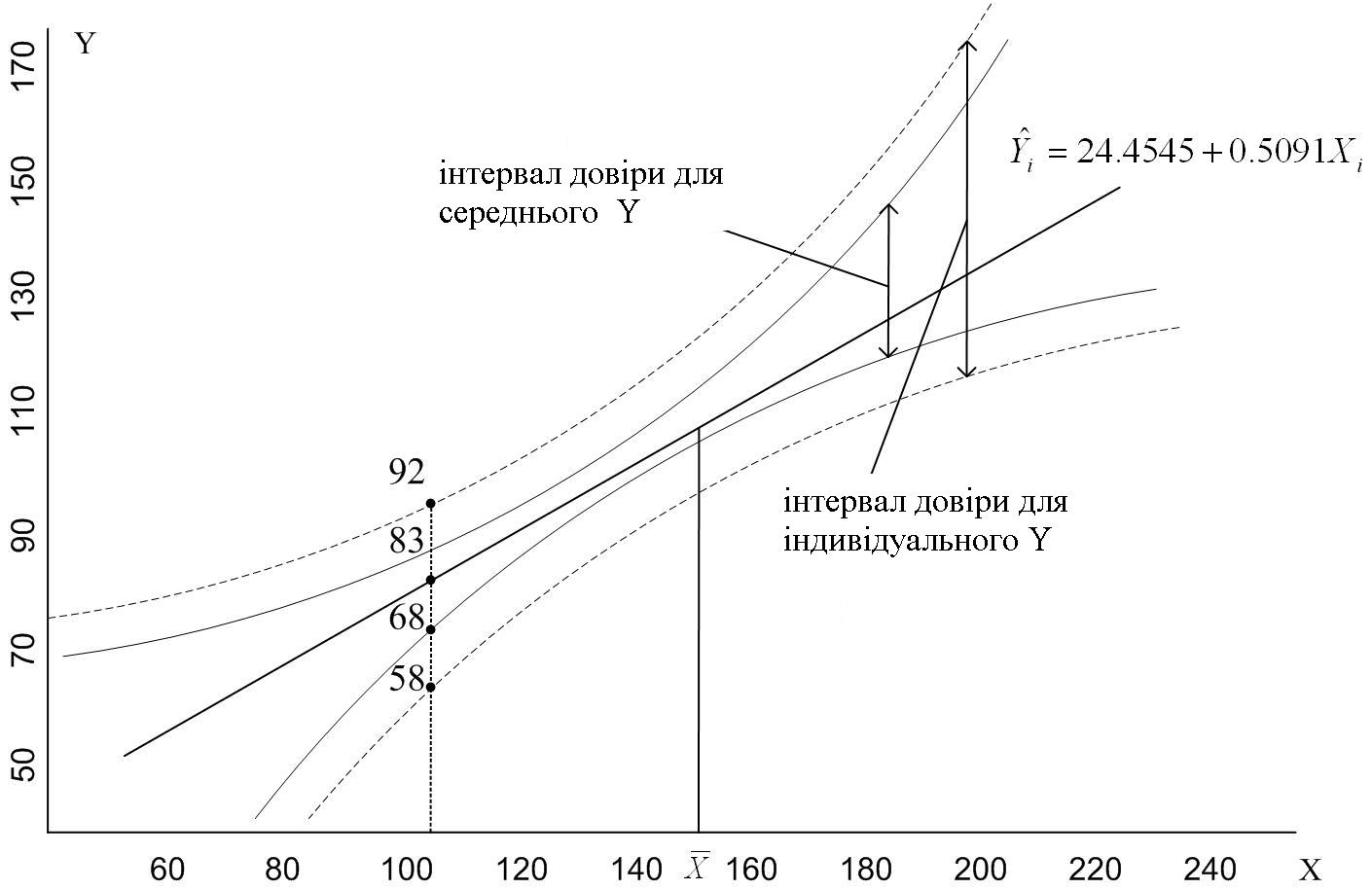
Рис. 3.6. Довірчі інтервали (області) для середньої Y й індивідуальної величини Y

Індивідуальний прогноз

Якщо нас цікавить індивідуальний прогноз величини Y для Y₀, відповідної заданій величині Х₀, то краща лінійна незміщена оцінка Y₀ також подається формулою (3.6.1), але її дисперсія має вигляд

.

(3.9.7)

Можна показати, що Y₀ також підкоряється нормальному закону розподілу з математичним сподіванням і дисперсією, заданими формулами (3.6.1) і (3.6.6) відповідно. Підставляючи замість невідомої можна показати, що

,

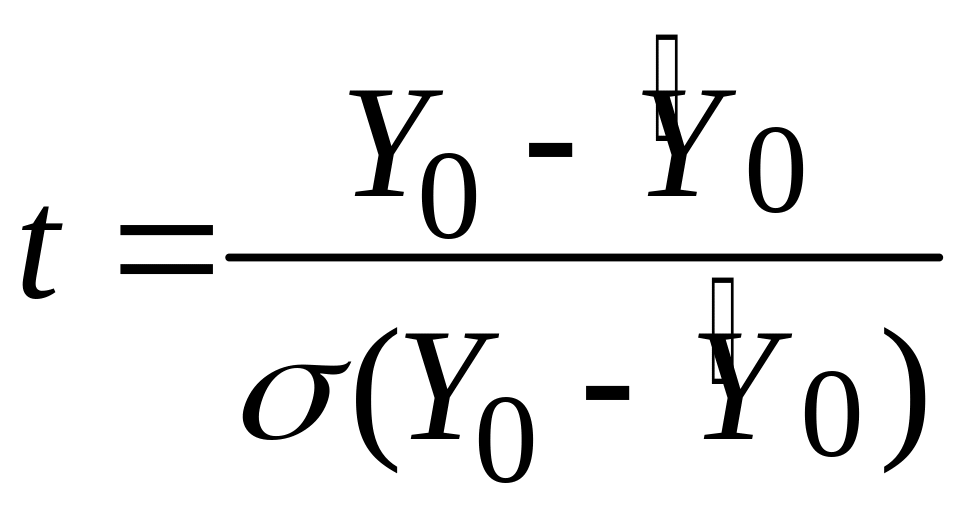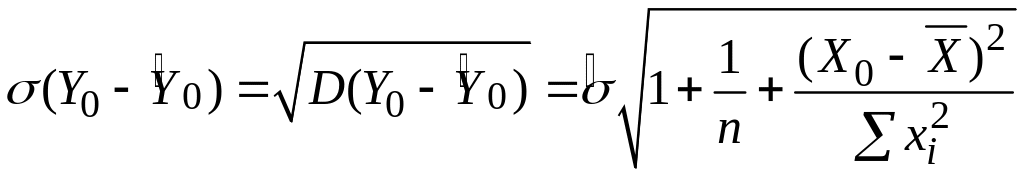
також підкоряється розподілу Ст’юдента. Отже, цей закон розподілу може бути застосований для висновку про істинне значення Y_0. Продовжуючи дослідження моделі “споживання  дохід”, ми знаходимо, що прогнозована точка Y₀=75,3645 така ж, як і , і її дисперсія є

,

.

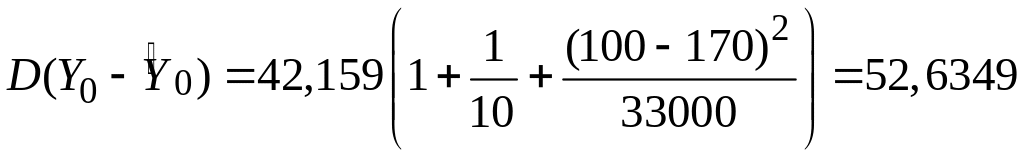Отже, 95%-й довірчий інтервал для Y₀, відповідного Х₀=100, визначається таким чином:

.

(3.9.8)

Порівнюючи цей інтервал з (3.6.5), ми бачимо, що довірчий інтервал для індивідуального Y₀ ширший, ніж за тих же умов довірчий інтервал для середнього значення E(Y|X₀). Обчисливши подібні довірчі інтервали для різних значень Х з табл. 1.3, ми отримаємо 95%-ву довірчу область для індивідуальних значень Y при даних значеннях Х. Ця довірча область зображена на рис.3.6, як і довірча область для .

Звернемо увагу на важливу властивість довірчих областей, зображених на рис.3.6. Ширина цих областей найменша при (див. вирази для дисперсій і доданок у них 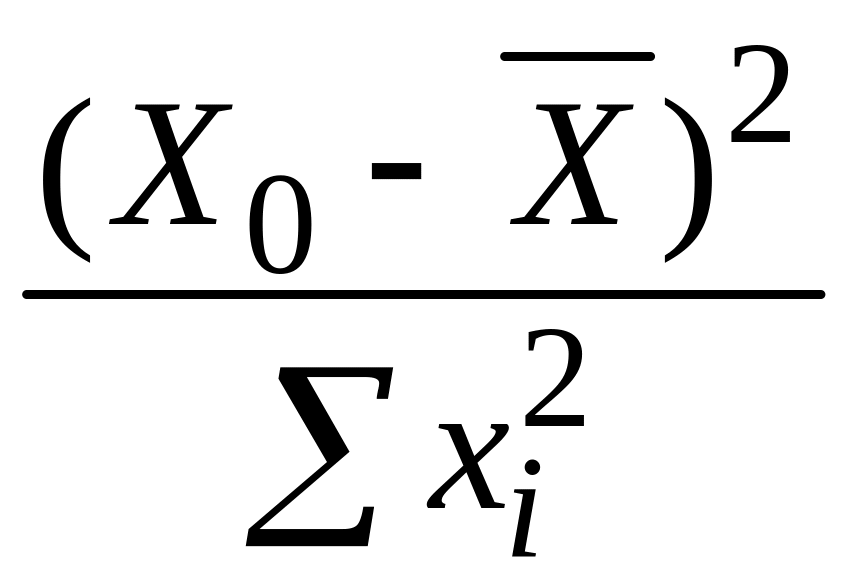). Ширина областей довіри збільшується в міру віддалення Х₀ від . Така поведінка свідчить про те, що здатність прогнозу зменшується в міру віддалення Х₀ від .

Отже, потрібно дуже обережно екстраполювати лінії історичної регресії для прогнозу E(Y|X₀) або Y₀ для заданого Х₀, що знаходиться на значній відстані від – середнього значення за вибіркою.
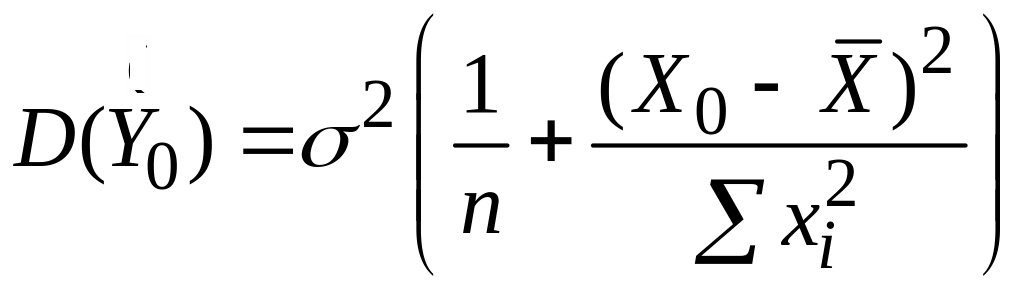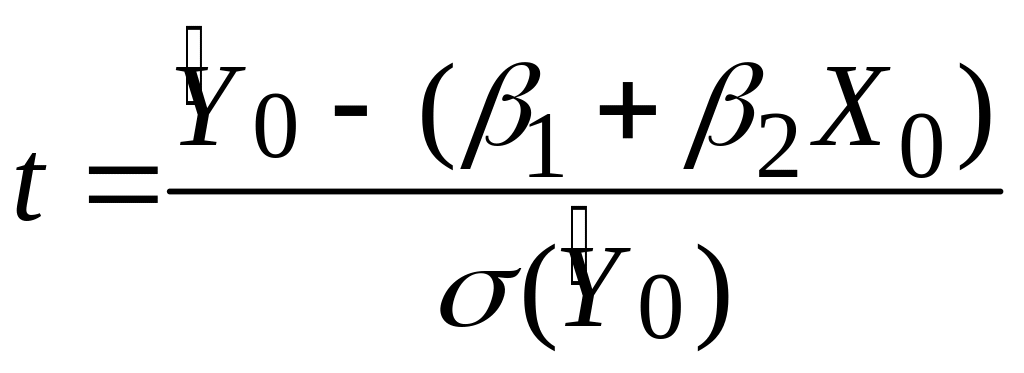
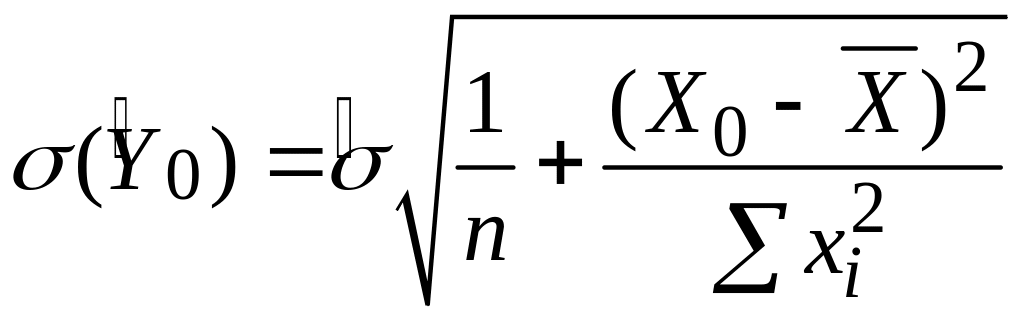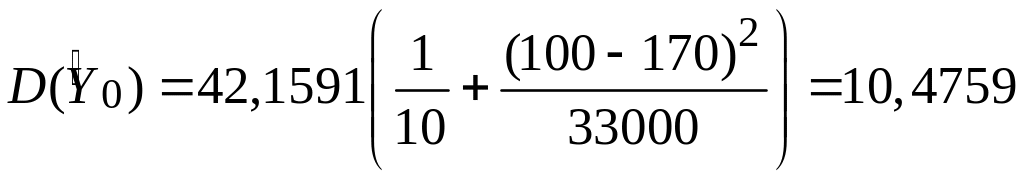
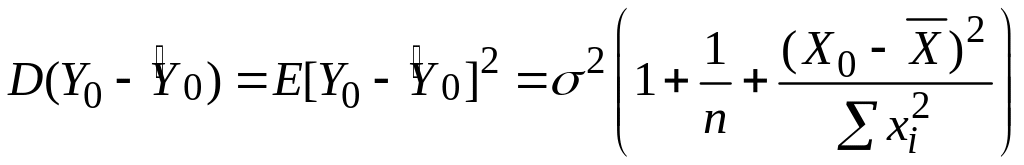