4.3. Функціональний вид регресійної моделі

Як ми відзначали раніше, розглядувані нами регресійні моделі повинні бути лінійні за параметрами. При цьому вони можуть і не бути лінійними за змінними. У наступних розділах буде приділена увага широко застосовуваним регресійним моделям, які можуть бути нелінійними за змінними, але лінійними за параметрами. Зокрема, розглядатимуться такі моделі:

1) лінійно-логарифмічна;

2) напівлогарифмічна;

3) зворотні.

4.4. Вимірювання еластичності. Лінійно-логарифмічна модель

Розглянемо експоненціальну регресійну модель

,

(4.4.1)

яка після логарифмування обох частин може бути подана у вигляді

.

(4.4.2)

Якщо ми запишемо (4.4.2) у вигляді

,

(4.4.3)

де , то побачимо, що ця модель лінійна за параметрами і , а також за логарифмами змінних Х і Y. Отже, для знаходження і може бути застосований МНК. Така модель ще називається “подвійною логарифмічною” або “логарифмічною лінійною”.

Якщо припущення класичної лінійної регресійної моделі виконуються, то параметри (4.4.3) можуть бути оцінені за МНК із рівняння

,

(4.4.4)

де , . Отримані за МНК оцінки і будуть найкращими незміщеними лінійними оцінками для і , відповідно.

Перевагою цієї моделі є те, що кутовий коефіцієнт є мірою еластичності Y по відношенню до Х, тобто визначає відсоток зміни Y для даного (малого) відсотка зміни Х. Так, якщо Y зображує попит на товар, а Х – ціну одиниці товару, то вимірює величину еластичності попиту за ціною, параметр lnY, що становить в економіці значний інтерес.

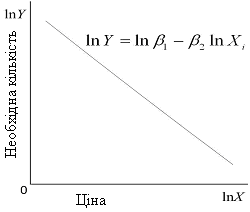
Рис. 4.2 . Експоненціальна модель Рис. 4.3. Лінійно-логарифмічна модель

Якщо співвідношення між величиною попиту і ціною таке, як зображено на рис. 4.2, то подвійне логарифмічне перетворення даватиме оцінку еластичності ціни ( ).

Слід зазначити два особливі моменти лінійної логарифмічної моделі: ця модель припускає, що коефіцієнт еластичності між Y і Х ( ) залишається постійним на всьому проміжку зміни Х. Цю властивість можна перевірити, оскільки еластичність Y по Х обчислюється за формулою

.

Якщо підставити в неї , то отримаємо

.

Ця властивість пояснює, чому дана модель називається моделлю з постійною еластичністю. Іншими словами, зміна lnY при одиничній зміні lnХ, тобто еластичність , залишається незмінною незалежно від точки lnX, в якій проводиться вимірювання (рис.4.3). Іншою особливістю моделі є те, що, хоча і є незміщеними оцінками і , (параметр, що входить у початкову модель ) є зміщеною оцінкою. У більшості практичних задач, проте, цей член має другорядне значення і немає необхідності в отриманні незміщеної оцінки.

Ілюстративний приклад. Попит на каву

Провівши обчислення за даними, наведеними в таблиці, одержуємо такий результат:

=0,7448 (0,0152) (0,0494) = 26,27 t = (51,0045) (–5,1251)

(4.4.5)

де Yt – попит на каву (кількість випитих чашок кави за день), а Xt – ціна на каву в доларах за фунт кави.

З цих результатів ми бачимо, що коефіцієнт еластичності ціни дорівнює –0,25. Це значить, що при зростанні на 1% реальної ціни за фунт кави, попит на неї зменшиться в середньому на 0,25%. Оскільки еластичність ціни менше 1 за абсолютною величиною, ми можемо сказати, що попит на каву нееластичний за ціною.

Цікавим є наступне питання. Чи можемо ми визначити, яка з моделей є кращою, порівнюючи результати лінійної та лінійно-логарифмічної функції попиту? Чи можемо ми сказати, що (4.4.5) краще, ніж (3.7.1), оскільки її вище (0,7448 проти 0,6628)? На жаль, ми не можемо зробити такий висновок, оскільки в тому випадку, коли залежна змінна у двох моделях неоднакова (тут Y і lnY), коефіцієнти детермінації безпосередньо порівнювати не можна. Ми не можемо порівнювати два кутових коефіцієнти ще й з іншої причини. Для моделі (3.7.1) кутовий коефіцієнт дає ефект одиничної зміни ціни на каву, скажемо на 1 дол. за фунт, на постійну абсолютну величину зменшення споживання, що складає 0,4795 чашки кави за день. З іншого боку, коефіцієнт –0,2530, отриманий в (4.4.5), дає постійне процентне зменшення споживання кави в результаті 1%-го зростання ціни на каву за фунт, тобто дає еластичність ціни.

Чи можна порівняти результати двох використаних моделей? Одним із шляхів порівняння двох моделей є наближене визначення еластичності ціни для моделі (2.7.1). Це може бути зроблено таким чином.

Еластичність Е змінної Y по відношенню до іншої змінної Х визначається за формулою:

.

(4.4.6)

Для лінійної моделі (2.7.1) оцінка кутового коефіцієнта дорівнює –0,4795. Як показано в (4.4.6), для знаходження еластичності необхідно помножити кутовий коефіцієнт на відношення Х/Y (ціни до кількості). Але які величини Х і Y повинні ми вибрати? Звичайно, ми можемо підрахувати еластичність для кожної з 11 пар значень Х і Y. На практиці, проте, еластичність підраховується в середніх значеннях Х і Y. Ми одержуємо оцінку середньої еластичності. Для нашого прикладу чашки і дол. Використовуючи ці величини і , одержуємо з (4.4.6) середню еластичність –0,2197 або наближено –0,22. Цей результат отриманий із лінійної моделі й відрізняється від коефіцієнта еластичності –0,25, отриманого в лінійній логарифмічній моделі. Зазначимо, що цей коефіцієнт еластичності є постійним у всіх точках Х, тоді як у лінійній моделі коефіцієнт еластичності змінюється від точки до точки.
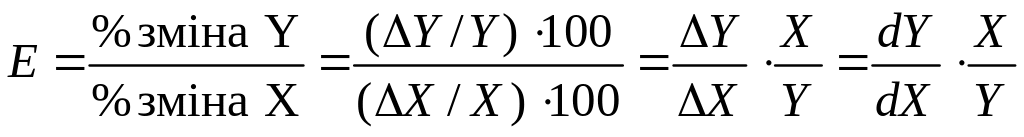