Можна показати, що при виконанні згаданих припущень

(7.5.4)

розподілено за законом F-розподілу з k і (n₁+n₂–2k) степенями вільності. Якщо значення F більше критичного значення для вибраного рівня значення , то ми відхиляємо гіпотезу про те, що регресії (7.5.1) і (7.5.2) збігаються, тобто гіпотезу про структурну стабільність. Можна застосувати альтернативний підхід. Якщо відповідна F p-величина мала, то ми відхиляємо гіпотезу про структурну стабільність.

Звернемося до нашого прикладу, врахувавши, що n₁=n₂=9.

(0,1452) (0,0088) R^2=0,9185 t = (–7,4548) (13,4316) s1=0,5722 DF=16.

Реконструктивний період:

(0,3054) (0,0266) R^2=0,3092 t = (–0,8719) (1,7700) s2=0,1396 DF=7.

Постреконструктивний період:

(0,3576) (0,0175) R^2=0,9131 t = (–4,8948) (8,5749) s3=0,1931 DF=7. s4=0,3327, s5=0,2395, F=5,04.

Якщо вибрати 5%-й рівень значущості, то можна визначити, що F_2,14=3,74. Оскільки значення величини F=5,04 більше критичного значення F, то ми маємо підставу відхилити гіпотезу про структурну стабільність функції заощаджень за два періоди. Обчислена величина p=0,0224 виявляється достатньо малою.

7.6. Перевірка функціонального виду регресії. Вибір між лінійною моделлю регресії і лінійно-логарифмічною моделлю

Вибір між лінійною моделлю регресії і лінійно-логарифмічною моделлю є постійним питанням емпіричного аналізу. Для вибору між цими моделями можна застосувати MWD-тест.

Розглянемо дві такі гіпотези:

Н₀: лінійна модель: Y – лінійна функція регресорів Х.

Н₁: лінійна логарифмічна модель: lnY – лінійна функція регресорsв lnХ.

Етапи MWD-тестування:

1. Проводимо оцінку лінійної моделі й отримаємо оцінену величину Y, назвемо її Y_f, тобто .

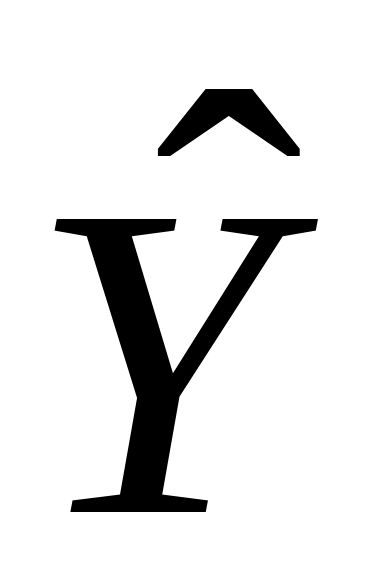2. Проводимо оцінку лінійної логарифмічної моделі й одержуємо оцінену величину lnY, назвемо її ln_f (тобто ).

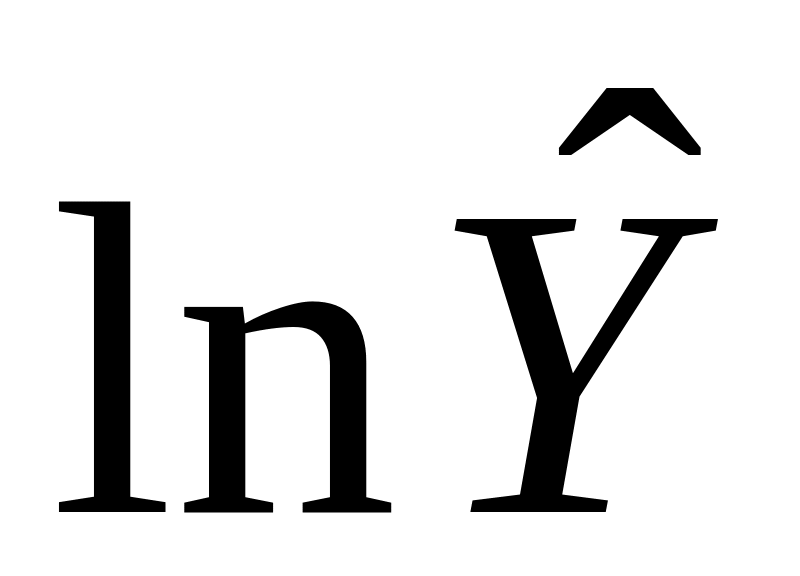3. Одержуємо Z₁=(lnY_f–ln_f).

4. Виконуємо регресію Y за X і Z₁, отриманими на етапі 3. Відхиляємо гіпотезу H₀, якщо коефіцієнт при Z₁ статистично значимий за звичайним t-тестом.

5. Одержуємо Z₂=exp(lnY_f–Y_f).

6. Виконуємо регресію Y за lnX і Z₂. Відхиляємо гіпотезу Н₁, якщо коефіцієнт при Z₂ статистично значущий за звичайним t-тестом.

8. Прогнозування в разі множинної регресії

У розд.5 ми показали, як оцінена модель двовимірної регресії може бути застосована для середнього прогнозу, тобто прогнозування для функції популяції регресії (PRF), а також для індивідуального прогнозу, тобто прогнозування індивідуального значення величини Y для фіксованого значення регресора X₀.

Оцінене рівняння множинної регресії також може бути використане для прогнозу. Його методика є простим поширенням двовимірного випадку й ґрунтується на тих же формулах за винятком формул для оцінок дисперсії і стандартних похибок прогнозованих величин.

Проілюструємо це на прикладі середнього й індивідуального прогнозів для моделі особистих витрат на споживання в США в 1956–1970 рр.:

(13,0261) (0,0487) (0,8486) R^2=0,9988,

(8.1)

де Y – особисті витрати на споживання; X₂ – особистий дохід; X₃ – змінна тренда.

Як нам відомо є оцінка величини істинного середнього значення Y для заданих значень X₂ і X₃.

Припустимо, що для 1971 р. маємо X₂=567 і X₃=16. Підставляючи ці значення в (8.1), одержуємо

.

(8.2)

Отже, середні особисті витрати на споживання для 1971 р. складають приблизно 509 млрд дол. Із причин, указаних раніше, 509 млрд дол. також є індивідуальним прогнозом для 1971 р., тобто Y₁₉₇₁. Проте дисперсії для середнього й індивідуального Y₁₉₇₁ прогнозів різні. Для їх обчислення найзручніше використовувати матричний апарат. Можна показати, що

і ;	(8.3)
і .	(8.4)

При виконанні припущень класичної моделі регресії ми тепер можемо побудувати 10(1–)-довірчий інтервал для середнього прогнозу:

.

Зрозуміло, що подібну процедуру можна виконати й для будь-яких інших значень Х₂ і Х₃.

100(1–)-довірчий інтервал для індивідуального прогнозу Y₁₉₇₁ складає

.

Для нашого прикладу ми одержуємо довірчий інтервал для середнього прогнозу

.

Довірчий інтервал для індивідуального прогнозу має вигляд

.

Кількість степенів вільності для t_/2 є (n–3) для моделі з трьома змінними і (n–k) для моделі з k змінними.