3.1.2.2. Анализ параметров точности механической обработки методом

математической статистики

1. Виды погрешностей. Все первичные (элементарные) погрешности обработки можно разделить на систематические постоянные, систематические переменные и случайные. Систематическими постоянными погрешностями называют такие, которые при обработке партии заготовок постоянны по значению и знаку. Систематическая постоянная погрешность появляется, например, вследствие погрешности в размере режущего инструмента (зенкера, развертки и др.) или в результате неточности профиля фасонного резца, протяжки и др. Систематическими переменными погрешностями называют такие, которые в процессе обработки закономерно изменяются по времени, т. е. в зависимости от числа изготовленных изделий. К этой группе относится погрешность, вызываемая износом режущего инструмента, и погрешность, обусловленная тепловыми. деформациями элементов технологической системы в период работы станка. Случайными погрешностями называют такие, которые для заготовок данной партии имеют различные значения, причем появление таких погрешностей и точное их значение заранее предсказать невозможно. К случайным относятся погрешность установки заготовки, погрешность установки режущего инструмента при наладке станка, погрешность, обусловленная упругими отжатиями элементов технологической системы. Например, изменения значений упругих отжатий элементов зависят от неравномерной твердости заготовок, от колебаний припуска на обработку, которые носят случайный характер.

2. Вероятностно-статистический метод оценки точности. Этот метод основан на проведении обработки опытной партии заготовок с замерами интересующего размера шкальным инструментом (микрометром или другим в зависимости от требуемой точности измерений). Результаты замеров математически обрабатывают, после чего строят кривую распределения исследуемого размера. Для этого в полученном ряде размеров выявляют предельные значения. Разность между наибольшим и наименьшим действительными размерами заготовок в данной партии ∆р называют размахом распрёделения, или полем рассеяния размеров:

∆р=l_max-_lmin.

Полученное значение ∆р разбивают на равные интервалы и определяют частоту повторения отклонений размеров в каждом интервале:

W_i=m_i/n,

где m_i — число заготовок, фактический размер которых находится в пределах данного интервала; п—общее число деталей в партии.

Далее строят график (полигон) распределения размеров. По оси абсцисс откладывают фактические размеры заготовок (или интервалы размеров), а по оси ординат—частоту их повторения. Например, на графике, приведенном на рис.3.5, а общее число деталей в исследуемой партии составляет 100 шт. Поле рассеяния размеров ∆_р = 0,16 мм. Для построения полигона размеров принято восемь размерных групп с интервалом в 0,02 мм. В первой размерной группе оказалось 5 деталей, т. е. частота ω₁= 0,05, во второй группе —13, т.е. частоты ω₂ = 0,13, и т.д. Полученные точки соединяют прямыми.

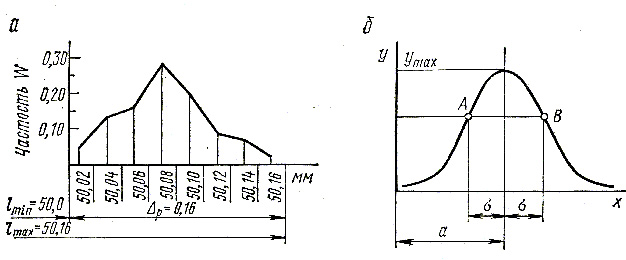Р и с. 3.5. Полигон и кривая распределения размеров

Если увеличить число размерных групп (например, принять интервал в 0,01 мм) и увеличить общее число обрабатываемых деталей, то ломаная линия становится более плавной.

Экспериментально установлено, что при обработке заготовок на металлорежущих станках способом автоматического получения размеров точность обработки подчиняется в большей или меньшей степени закону нормального распределения, который изображается математической кривой Гаусса (см. рис. 3.5,б), уравнение которой

,

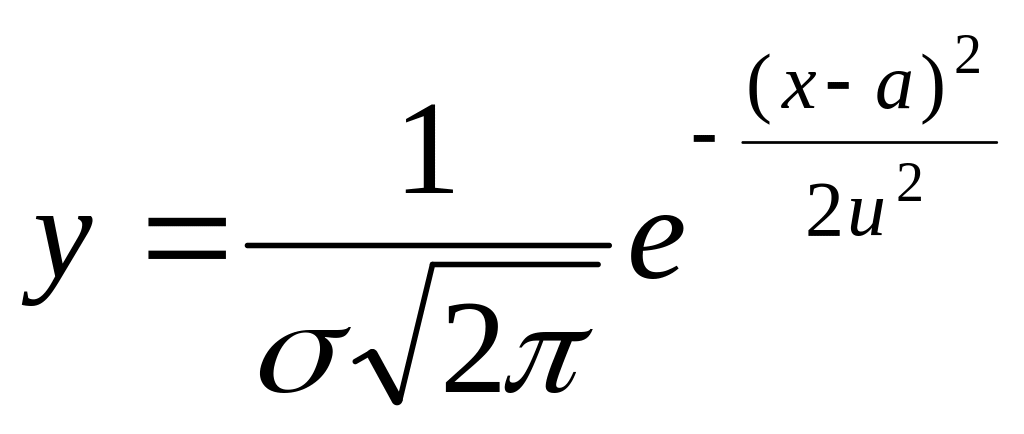где σ — среднее квадратичное отклонение аргумента; е — основание натуральных логарифмов; параметр а является центром группирования значения аргумента и в то же время его средней арифметической.

Среднее квадратичное отклонение σ определяют по результатам измерений партии заготовок по формуле

,

где п — число произведенных измерений; xi — значение текущего измерения; Х_ср — среднее арифметическое данных измерений:

.

Число измерений п следует брать 50 или более. При меньшем n погрешность определения σ превышает ± 10 %.

Кривая нормального распределения симметрична. Ордината вершины кривой Ymax будет при х =a; она определяется из выражения

.

Кривая имеет точки перегиба на расстояниях х == ± σ. Их ординаты равны

.

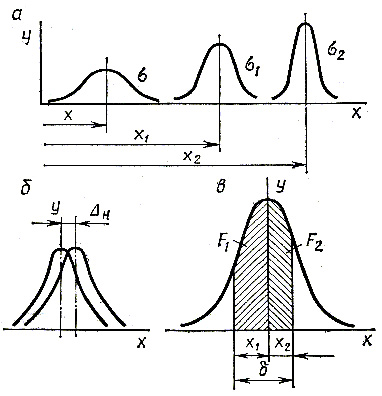
Р и с. 3.6. Закономерности изменения кривых распределения размеров

Величина σ характеризует форму кривой распределения и является мерой точности данного метода обработки. При увеличении σ вершина кривой снижается, но ветви кривой растягиваются, т. е. поле рассеяния размеров растет. При уменьшении а ордината кривой возрастает, а поле рассеяния сужается. На рис.3.6,а схематически показаны кривые распределения диаметральных размеров при обработке партии заготовок последовательно после предварительного точения (кривая σ), чистового точения (кривая σ1) и шлифования (кривая σ2), причем при правильном построении этапов процессов необходимо выполнение условия

σ > σ1 > σ2

Если обрабатываются две партии одноименных заготовок, то появляется систематическая постоянная погрешность, связанная с погрешностью настройки станка на размер или с различными отклонениями размеров режущего инструмента. В этом случае кривые распределения погрешностей при обработке первой и второй партий будут смещены одна относительно другой на размер постоянной погрешности ∆н (рис.3.6,б).

Изучение кривых распределения погрешностей позволяет выявить соотношение между числом годных и бракованных деталей. Предположим, что на обработку заготовок установлен допуск δ. На оси абсцисс (см. рис.3.6,в) этот допуск определяется величинами X1 и Х2 от границ центра группирования. Заштрихованный участок соответствует числу заготовок, находящихся в пределах поля допуска. Отношение площади этого участка к общей площади, ограниченной кривой, определяет вероятность получения годных заготовок, так как площадь, ограниченная кривой нормального распределения соответствует общему числу заготовок в партии.

Площади F1 и F2 рассчитывают по формулам

;

.

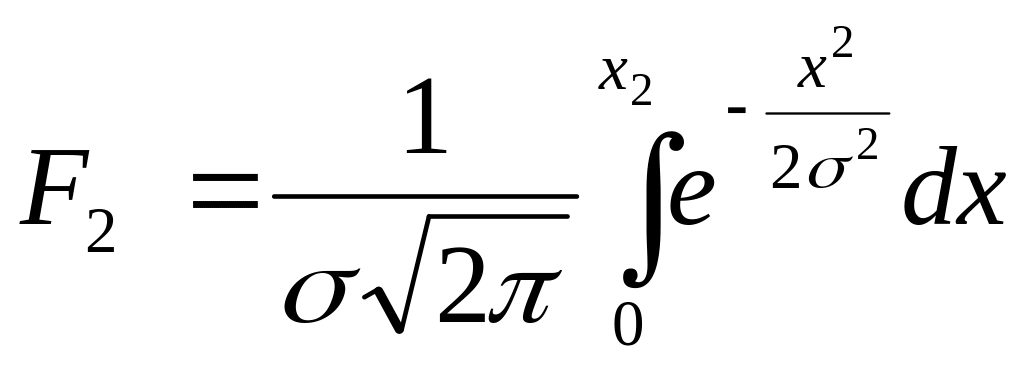Если принять x/σ = z, то эти интегралы можно представить в виде функции Ф (z):

;

.

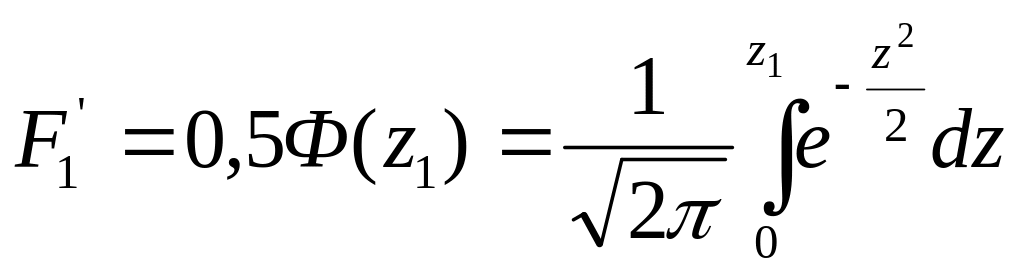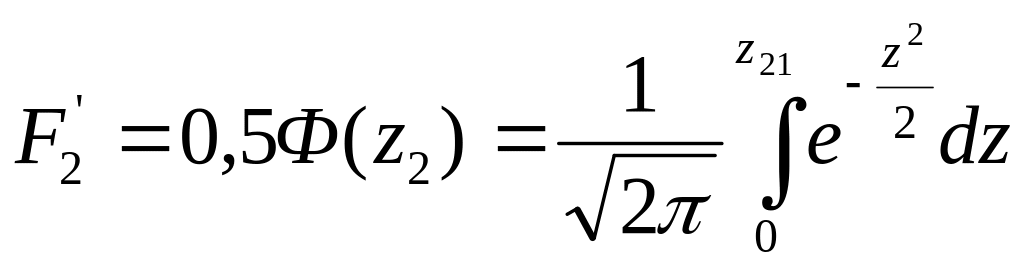Вся площадь, ограниченная кривой, равна 1. Значения величин F'1 и F’2 меньше единицы. Значения функции Ф (z) через десятую долю аргумента приведены в табл.3.1.

Из табл. 3.1 видно, что в интервале z= ± 3, т. е. при x=±3σ площадь, ограниченная этим участком кривой, составляет 0,9973 всей площади. Это означает, что 99,73 % всех обработанных заготовок, находящихся в интервале 6σ, будут годными, и процент брака не превысит 0,27%.

Таким образом, определив для исследуемого процесса значение σ, можно установить точность данного метода обработки по величине 6σ (правило «шести сигм»). Если принять для расчета, например, величину 5σ, то процент брака возрастет до 1,24, так как согласно табл. 3.1 Ф(z) будет 0,9876. Возрастание вероятности брака почти в 4,5 раза недопустимо.

Правило шести сигм является достаточно точным для практических расчетов. Рассмотрим с этой целью два примера.

Таблица 3.1.

Z	Ф(z)	z	Ф (z)	z	Ф (z)
0	0	1,2	0,7699	2,4	0,9836
0,1	0,0797	1,3	0,8064	2,5	0,9876
0,2	0,1585	1,4	0,8385	2,6	0,9907
0,3	0,2358	1,5	0,8664	2,7	0,9931
0,4	0,3108	1,6	0,8904	2,8	0,9949
0,5	0,3829	1,7	0,9109	2,9	0,9963
0,6	0,4515	1,8	0,9281	3	0,9973
0,7	0,5161	1,9	0,9426	3,1	0,99806
0,8	0,5763	2	0,9545	3,2	0,99862
0,9	0,6319	2,1	0,9643	3,3	0,99903
1	0,6827	2,2	0,9722	3,4	0,99933
1,1.	0,7287	2,3	0,9786	3,5	0,99953

Пример 1. Установить вероятность брака деталей, если среднее квадратичное отклонение для исследуемого процесса σ= 0,015мм, допуск на обработку σ = 0,075 мм, а границы поля допуска (рис.3.6. расположены от центра группирования на расстояниях x1= 0,045мм и x2= 0,03 мм.

Решение. Определим значения z1 и z2:

z1=x1:σ =0,045: 0,015 = 3; z2=x2 : σ = 0,03 : 0,015 = 2.

По табл. 3.1. определим F’1 и F’2:

F’1 =0,5Ф(z1)=0,5▪0,9973=0,4986;

F’2 =0,5Ф(z2)= 0,5▪0,9545=0,4772.

Вероятность брака (в процентах)

P=[ 1-(F’1+F’2)]•100=(1-(0,4986+0,4772)]▪100=2,42%

Пример 2. Определить, как изменится вероятность брака деталей по условиям предыдущей задачи, если путем наладки технологической системы совместить центр группирования кривой распределения с серединой поля допуска.

Решение. Из условия

z1= z2 = z =δ/2: σ =0,075/2 :0,015=2,5.

Найдем по табл. 3.1. F’1 и F’2:

F’1= F’2 = 0,5Ф (z) = 0,4938.

Вероятность брака (в процентах)

P=[ 1-(F’1+F’2)]▪100 = [1- (0,4938+0,4938)]▪100=1,24%.

Следовательно, по сравнению с предыдущим примером вероятность брака уменьшится на 1,18%.

При изучении точности обработки кроме закона нормального распределения (закон Гаусса) встречаются и другие законы распределения размеров. Если размер обработки зависит только от действия одного фактора, изменяющегося по закону прямой, то распределение размеров подчиняется закону равной вероятности. Например, в верхней части рис.3.7,а показано, что возрастание размера х обработанной поверхности в результате постепенного износа режущего инструмента происходит по закону прямой х = аτ, где τ — время резания, а — постоянная величина, характеризующая интенсивность изнашивания резца; в нижней части этого рисунка приведена кривая распределения размеров в виде прямоугольника, соответствующая закону равной вероятности.

В том случае, когда размер х интенсивно возрастает в начальный период резания, затем его рост замедляется и вновь увеличивается (в конце стойкости режущего инструмента), что показано в верхней части рис.3.7,б кривая распределения размеров, показанная в нижней части этого рисунка, соответствует закону треугольника (закону Симпсона).

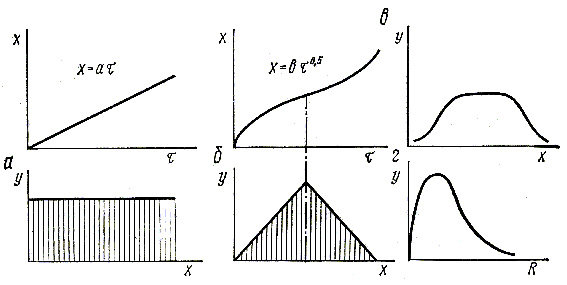
Р и с. 3.7. Законы распределения размеров

В случае совместного влияния на точность обработки закономерно изменяющейся погрешности, например износа режущего инструмента, подчиняющегося закону равной вероятности, и случайных погрешностей, подчиняющихся закону Гаусса, кривая распределения искажается. На рис.3.7,в в качестве примера показана композиция кривой Гаусса и кривой равной вероятности.

Рассеяние значений эксцентриситета, биения, дисбаланса и т. п. подчиняется закону Максвелла. Эти погрешности являются положительными величинами, изменяясь от нуля до определенного значения. На рис.3.7,г показана кривая распределения эксцентриситетов ступенчатых валов. Форма этой кривой несимметричная.

Метод оценки точности на основе кривых распределения универсален и позволяет объективно оценить точность механической обработки, сборочных, контрольных и других операций. Недостаток метода — невозможность выявить изменение изучаемого параметра во времени, т. е. последовательности обработки заготовок, что не позволяет осуществить регулирование хода технологического процесса. Кроме того, переменные систематические погрешности нельзя отделить от случайных; это затрудняет выявление и устранение причин погрешностей. От этих недостатков свободен метод статистического регулирования технологического процесса.

3. Статистическое регулирование технологического процесса. Под этим понимается корректировка параметров процесса в ходе производства с помощью выборочного контроля изготовляемой продукции для обеспечения требуемого качества и предупреждения брака. Для статистического регулирования процесса применяется метод медиан * и индивидуальных значений и метод средних арифметических значений и размахов.

Первый метод рекомендуется при отсутствии автоматических измерительных средств, второй — при наличии автоматических устройств для контроля (активный контроль).

Эти методы пригодны при погрешностях двусторонних (распределение по закону Гаусса) и односторонних (распределение по закону Максвелла). Рассмотрим применение этих методов при распределении параметров (размеров деталей) по закону Гаусса.

Р и с.3.8. Контрольная карта метода медиан и индивидуальных значений.

* Медианой x называется срединное значение упорядоченного по возрастанию или убыванию ряда чисел.

Метод медиан и индивидуальных значений(х, хi,).Из потока продукции через определенный промежуток. времени периодически отбирают выборку объемом 3—10 единиц. Чаще всего объем выборки принимают в 5 единиц. Период времени между двумя отборами выборок устанавливается опытным путем, зависит от стабильности процесса и обычно составляет 1 - 2 ч. Отобранные экземпляры измеряют шкальными инструментами.

При распределении погрешностей по закону Гаусса на карту (рис.3.8.) наносят результаты контроля. Карта имеет две внешние сплошные горизонтальные линии, ограничивающие поле допуска: Тв и Тн и четыре предупредительные: две — Рв и Рн, являющиеся границами для регулирования медиан, и еще две — Рв.р и Рн.р — для регулирования крайних значений данной выборки.

Положение предупредительных границ рассчитывается по формулам

Рв=Тв-0,8δ/2;

Рн=Тн+0,8δ/2;

Рв.р=Тв-Вδ/2;

Рн.р=Тн+Вδ/2,

где 0,8—поправочный коэффициент; А и В—коэффициенты, зависящие от объема выборки (при выборке п = 5 единиц А == 0,559, В = 1,63*); δ—допуск.

Далее на карту наносят результаты замеров в виде точек, за исключением третьего измерения (при п == 5), которое отмечается крестиком (согласно рис.3.8. например, результаты замеров в первой выборке 37,97; 37,97; 37,98; 37,99; 37,99; размер 37,98 является третьим и отмечается крестиком). Протекание процесса считается удовлетворительным, если медианы х не выходят за границы Рв и Рн, а крайние значения выборок — за границы Кв.р и Рн.р. При таком процессе продукцию, изготовленную между данной и предыдущей выборками, принимают без дополнительного контроля. Если же имеются выходы точек за границы регулирования, то процесс считается неудовлетворительным. Например, выборки 4, 5 и 6 вышли за границы Рв и Рв.р, а выборка 7 — за границы Рн и Рн.р. В этом случае дают сигнал предупреждения, на карте делают отметку в виде стрелки и устраняют причину, вызвавшую отклонение процесса от нормального хода. Продукция, изготовленная между двумя выборками, подлежит сплошному контролю.

Метод средних арифметических значений и размахов (х, R). При этом методе также отбирают выборки объемом 3—10 единиц. Отобранные экземпляры измеряют шкальными инструментами.

Статистическими характеристиками при этом методе являются среднее арифметическое значение х и размах варьирования R данной выборки, определяемые по формулам

х= ∑х_i/n,

где xi — результат замера контролируемого параметра; п — число замеров в выборке;

R = Х_наиб – Х_наим,

где Х_наиб и Х_наим — наибольшее и наименьшее значения в выборке.

Результаты замеров и расчетов значений х и R изображают графически. На рис.3.9. показан пример контрольной карты при распределении по закону Гаусса одного из показателей качества, регулируемого в пределах значений 60 — 65. В верхней части карты нанесены графически (•) средние арифметические значения х. Здесь Тв и Тн —две внешние границы поля допуска, а Рв и Рн —две внутренние, ограничивающие поле предупреждения.

В нижней части карты отложены значения размаха варьирования R и нанесены три границы: верхнего предела допуска ТвR, нижней сплошной границы, обычно принимаемой равной нулю, и верхней границы урегулирования РвR..

При удовлетворительном протекании процесса средние арифметические значениях выборок не должны выходить за границы регулирования Рв и Рн, а размахи R—за свою границу РвR. Предупредительные границы регулирования сигнализируют о возможности возникновения брака. Из рис.3.9. видно, что выборки 4, 5 и 6 сигнализируют о разладке процесса.

Границы Рв и Рн определяют по формулам

Рв=Тв – Аδ/2 и Рн=Тн+Аδ/2,

где δ —допуск;

А — коэффициент, зависящий от объема выборки (при n = 5 А= 0,553).

Границу для размахов определяют по формуле

РвR=Bδ/2,

где В — коэффициент, зависящий от объема выборки (для п=5 В=1,63).

(Коэффициенты А и В определяют на основе теоретических положении статистического контроля).

Р и с. 3.9. Контрольная карта метода средних арифметических значений и размахов.