7. Прогнозирование нагрузок

Одной из достаточно сложных задач развития ЭЭС является прогнозирование нагрузок и электропотребления. Здесь сильно сказывается вероятностный характер и неопределенность исходных данных, поэтому существует определенный скепсис к формализованным методам прогнозирования. Однако эти методы позволяют осуществить обработку больших объемов информации и выявить существующие тенденции прогнозируемых показателей.

Как правило, процедура прогнозирования подразделяется на два этапа:

• предварительный анализ и интерполяция статистических временных зависимостей;

• экстраполяция и коррекция выбранной математической функции прогноза.

Предварительный анализ временной зависимости

На этапе предварительного анализа определяется общий вид моделирующих функций, или, как их называют, функций-предикторов, и определяется масштаб моделирования значений временного ряда (иногда желателен переход к логарифмическому масштабу).

Выбор математической модели зависит от сроков упреждения прогнозов: долгосрочные (свыше 10 лет); среднесрочные (5-10 лет); краткосрочные (1-3года); оперативные (от нескольких часов до года). При решении задач перспективного развития ЭЭС (свыше 5 лет) представляет интерес характер изменения годовых максимумов нагрузки энергосистемы. При планировании капитальных ремонтов основного оборудования ЭЭС - месячных максимумов, при планировании текущих ремонтов - суточных максимумов, при распределении нагрузки энергосистемы между параллельно работающими агрегатами и выборе состава работающего оборудования - часовых нагрузок.

При решении задач прогнозирования годовых максимумов нагрузки или годовых уровней электропотребления обычно используются многочлены Y(t)=a₀+a₁t+a₂t²+... .

Возможно также прогнозирование в пространстве ортонормированных многочленов. Если G_n- многочлен порядка n-1, то

Y(t)=a₀ G₀(t)+a₁ G₁(t)+a₂ G₂(t)+....

В прогнозах на перспективу часто используются нелинейные математические модели, например

Y(t)=a₀-a₁exp(-a₂t).

Моделирование месячных максимумов нагрузки выполняется на основе модели, учитывающей сезонные колебания прогнозируемого параметра

Y(t)=a₀+a₁t+a₂cos(2t/T),

где Т- период колебаний (например, равный одному году).

Прогнозирование связей между выработкой электроэнергии и некоторыми показателями спроса на нее выполняется на основе эконометрических моделей множественной регрессии:

.

Выбор той или иной математической модели и оценка ее параметров осуществляются на основании некоторого критерия, зависящего от того, насколько точно теоретическая функция описывает статистический ряд. Одним из таких критериев является сумма квадратов отклонений эмпирических данных от теоретических оценок. После выбора критерия решается оптимизационная задача определения параметров математической модели, минимизирующих критерий.

1. Метод наименьших квадратов

Задача 3.2. Методом наименьших квадратов оценить коэффициенты {a_i} полинома

y(t)=a0+a1t+a2t^2+a3cos(2πt/T),

(3.0)

интерполирующего заданный эмпирический временной ряд.

Решение представлено в таблицах рис. 3.14, 3.15. В строке А23:Е23 задаются начальные значения параметров. В строке В27:К27 представлен ряд наблюдений. В строке 26 по формуле ( 3 .0) вычисляются теоретические значения функции Y(t). Строка 28 представляет разность строк 26 и 27. В ячейке L28 записана формула =СУММКВ(B28:K28) расчета суммы квадратов отклонений теоретических значений от наблюдаемых.

При оптимизации минимизируется значение ячейки L28 в ходе изменения содержимого ячеек А23:Е23. Исходная таблица оптимизации представлена на рис. 3.14. Результирующая – на рис. 3.15. В результате аппроксимирующая функция имеет вид y(t)=-2,52+7,51t+10,7t²+7,2cos(2πt/2,39).

Отыскание параметров {a_i} выполняется с помощью операции Сервис/Поиск решения. При этом сумма квадратов отклонений составляет 1,6, что свидетельствует о достаточно хорошем приближении теоретической функции. Соотношение теоретической кривой и экспериментальных данных представлено на рис. 3.16.

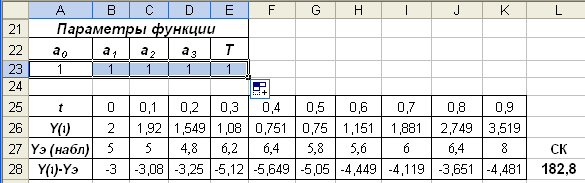
Рис. 3.62. Исходные параметры оптимизации

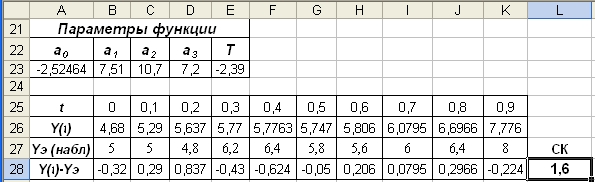
Рис. 3.63. Результирующая таблица наименьших квадратов

Д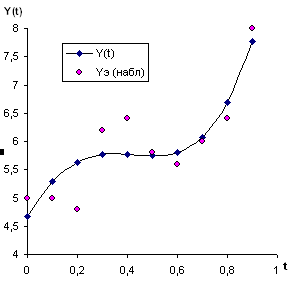анный подход может быть использован для интерполяции (экстраполяции) временного ряда любой сложной функцией, например рядом Фурье:

где Q(t) - полином, отражающий нециклический характер прогнозируемой величины; a_k, b_k, k=1,2,..- оцениваемые коэффициенты ряда.

Рис. 3.64. Интерполяция ряда данных