
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
Точки разрыва функции могут быть Ι рода (выполнено только условие 2 – «устранимый разрыв» или выполнено условие 1, причем в точке
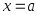 односторонние пределы конечны, но
различны – «скачок») или ΙΙ рода (предел
функции в точке
односторонние пределы конечны, но
различны – «скачок») или ΙΙ рода (предел
функции в точке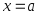 не существует либо хотя бы один из
односторонних пределов бесконечен).
не существует либо хотя бы один из
односторонних пределов бесконечен).Пример 2.1.
Исследовать функцию на непрерывность:
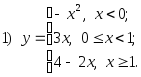
 .
.Решение.
1. Каждая из составляющих функций является элементарной, значит, каждая из них непрерывна во всех точках, в которых она определена. Точки, «подозрительные» на разрыв: х = 0, х = 1.
Пусть x = 0.
y(0) существует, у(0) = 3∙0 = 0.
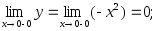

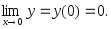
Следовательно, в точке х = 0 функция непрерывна по определению.
Пусть х = 1.
y (1) существует; у(1) = 2.


3 ≠ 2, следовательно, точка х = 1 является точкой разрыва 1-го рода (скачок).
2. D(y): x ≠ 1.
Т. к. в точке х = 1 функция не определена, то это точка разрыва.
 точка
разрыва второго рода.
точка
разрыва второго рода.2.10. Найти точки разрыва функций:
1)
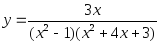 ;
2)
;
2)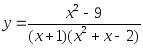 ;
;3)
 4)
4)
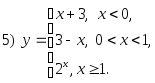
2.11. Исследовать функции на непрерывность:
1)
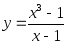 ;
2)
;
2)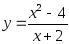 ;
3)
;
3)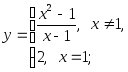
4)
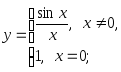 5)
5) ;
6)
;
6)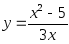 ;
;7)
 8)
8)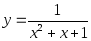 ;
;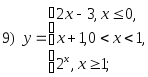
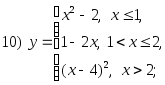
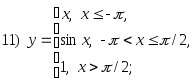
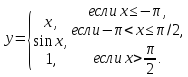

Контрольные задания
Вариант 1.
1. Найти пределы:

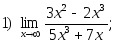

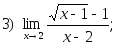
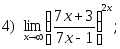
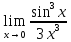

2. Исследовать на непрерывность и найти точки разрыва функции (указать их характер):
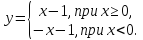

Вариант 2.
1. Найти пределы:
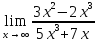
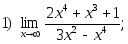
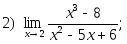
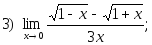
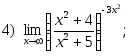
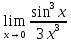

2. Исследовать на непрерывность и найти точки разрыва функции (указать их характер):
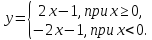
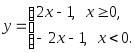
Вариант 3.
1. Найти пределы:

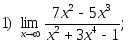
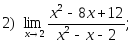
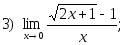
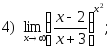
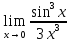
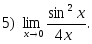
2. Исследовать на непрерывность и найти точки разрыва функции (указать их характер):
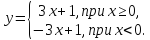
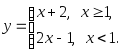
2.3. Производная и дифференциал
Определение. Производной функции f(х) называется предел отношения приращения функции к приращению аргумента при ∆х стремящемся к нулю, если этот предел существует:

Производные простейших функций:
1. (
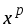 )'
=
)'
=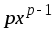 ;
частные случаи:
;
частные случаи: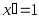 ;
(
;
(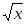 )'
=
)'
= .
.2. (
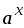 )'
=
)'
=
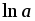 ;
частный случай:
;
частный случай:
3. (
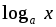 )'
=
)'
= ;
частный случай: (
;
частный случай: ( )'
=
)'
= .
.4. (sinx)' = cosx. 5. (cosx)' = − sinx.
6. (tgx)' =
 .
7. (ctgx)'
=
.
7. (ctgx)'
=
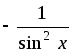 .
.8. (arcsinx)' =
 .
9. (arccosx)'
= –
.
9. (arccosx)'
= –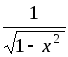 .
.10. (arctgx)' =
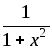 .
11. (arcctgx)'
= –
.
11. (arcctgx)'
= –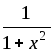 .
.Правила дифференцирования
1. Производная постоянной:

2. Производная суммы:
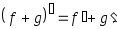
3. Производная произведения
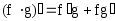 .
.Следствие:
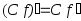 ,
т. е. постоянный множитель можно вынести
за знак производной.
,
т. е. постоянный множитель можно вынести
за знак производной.4. Производная частного:

5. Производная сложной функции:
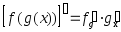 ,
,
где f = f(x), g = g(x) – дифференцируемые функции.
Пусть функция
 задана
параметрически:
задана
параметрически:

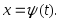 Тогда еепроизводная
равна
Тогда еепроизводная
равна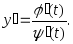
2.3.1. Примеры вычисления производных
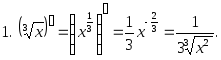

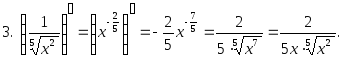

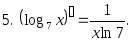
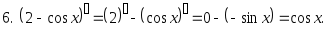
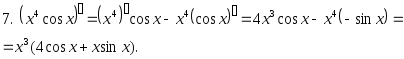
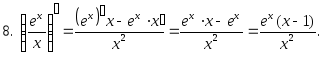
 ,
,

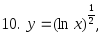
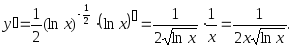
11. Найти производную функции, заданной неявно:
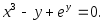
Решение.

2.12. Найти производную функции по определению производной:
1)
 2)
2)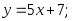 3)
3)
4)
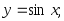 5)
5)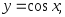 6)
6)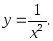
2.13. Найти производную функции:
1)
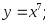 2)
2)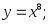 3)
3) 4)
4)
5)
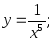 6)
6) 7)
7)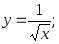 8)
8)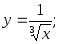
9)
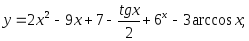
10)
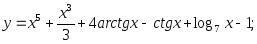
11)
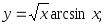 12)
12)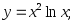 13)
13)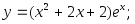
14)
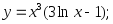 15)
15)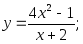 16)
16)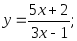
17)
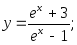 18)
18)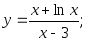 19)
19)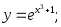
20)
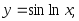 21)
21)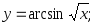 22)
22)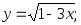
23)
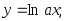 24)
24)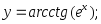 25)
25)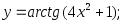 26)
26)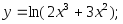 27)
27) 28)
28)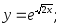
29)
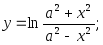 30)
30)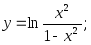 31)
31)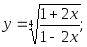
32)
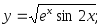 33)
33)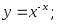 34)
34)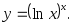
2.14. Найти производную функции и вычислить ее значение при x = x0:
1)
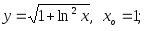 2)
2)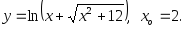
2.15. Найти производные функций, заданных неявно:
1)
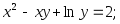 2)
2)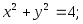
3)
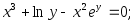 4)
4)
2.16. Найти производную n-го порядка функций:
1)
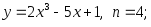 2)
2)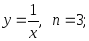
3)
 4)
4)

2.3.2. Применение производной в экономике
2.17. Объем продукции u (ед.) в течение рабочего дня представляет функцию u =
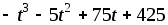 ,
гдеt
– время (ч). Найти производительность
труда, скорость и темп ее изменения
через 2 часа после начала работы; за 1
час до ее окончания (при 8-часовом
рабочем дне).
,
гдеt
– время (ч). Найти производительность
труда, скорость и темп ее изменения
через 2 часа после начала работы; за 1
час до ее окончания (при 8-часовом
рабочем дне).2.18. Зависимость между издержками производства y (ден. ед.) и объемом выпускаемой продукции х (ед.) выражается функцией:
а)
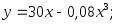 б)
б)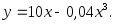
Определить средние и предельные издержки при объеме продукции, равном 5 ед.
2.19. Зависимость между себестоимостью продукции С и объемом Q ее производства выражается формулой
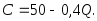 Определить эластичность себестоимости
при выпуске продукции, равном 30.
Определить эластичность себестоимости
при выпуске продукции, равном 30.Указание. Эластичность функции y(x) равна
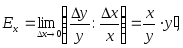
где
 и
и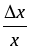 − относительные приращения функции
и аргументов соответственно. Эластичность
функции показывает приближенно, на
сколько процентов изменится функцияy
= f(x)
при изменении аргумента x
на 1 %.
− относительные приращения функции
и аргументов соответственно. Эластичность
функции показывает приближенно, на
сколько процентов изменится функцияy
= f(x)
при изменении аргумента x
на 1 %.2.20. Функции спроса q и предложения s от цены p выражаются соответственно уравнениями: 1) q = 7 − p, s = p + 1; 2)


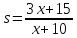
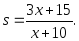
Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на 5 % от равновесной.
2.21. Функции спроса q и предложения s от цены p выражаются соответственно уравнениями q = 9 − p и s = p + 2.
Найти: а) равновесную цену; б) эластичность спроса и предложения для этой цены; в) изменение дохода (в процентах) при увеличении цены на 10 % от равновесной.
2.22. Функции долговременного спроса q и предложения s от цены p на мировом рынке нефти имеют соответственно вид: q = 30 − 0,9p, s = 16 + 1,2p.
1. Найти эластичность спроса в точке равновесной цены.
2. Как изменятся равновесная цена и эластичность спроса при уменьшении предложения нефти на рынке на 25 %?
2.23. Зависимость между себестоимостью готовой продукции предприятия у (млн руб.) и объемом выпускаемых изделий х (тыс. шт.) выражается уравнением
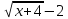
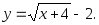 Найти
эластичность себестоимости продукции
предприятия, выпускающего 12 тыс. шт.
изделий. Какие рекомендации можно дать
руководителям предприятий об изменении
величины объема выпускаемой продукции?
Найти
эластичность себестоимости продукции
предприятия, выпускающего 12 тыс. шт.
изделий. Какие рекомендации можно дать
руководителям предприятий об изменении
величины объема выпускаемой продукции?2.24. Зависимость потребления y от дохода x задается функцией
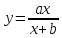
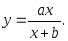 Показать, что эластичность функции
потребления от дохода не зависит от
параметраа
и стремится
к нулю при неограниченном возрастании
дохода.
Показать, что эластичность функции
потребления от дохода не зависит от
параметраа
и стремится
к нулю при неограниченном возрастании
дохода.2.25. Функция потребления некоторой страны имеет вид:
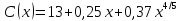
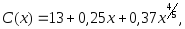 гдеx
− совокупный
национальный доход.
гдеx
− совокупный
национальный доход.Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 32.
2.26. Функция сбережения некоторой страны имеет вид:

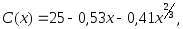 гдеx
– совокупный национальный доход.
гдеx
– совокупный национальный доход.Найти: а) предельную склонность к потреблению; б) предельную склонность к сбережению, если национальный доход составляет 27.
2.27. Функция спроса q от цены p описывается формулой
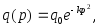 где
где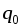 иk
– известные величины. Найти, при каких
значениях цены p
спрос будет эластичным.
иk
– известные величины. Найти, при каких
значениях цены p
спрос будет эластичным.2.28. Найти изменение выручки с увеличением цены на товар при разных вариантах эластичности спроса, если выручка V(р) равна произведению цены р на величину спроса q(р).
2.3.3. Дифференциал функции
Определение. Дифференциалом функции у = f(х) называется выражение

Применение дифференциала в приближённых вычислениях: при достаточно малых значениях
 х
х
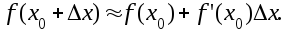
Пример 2.2.
Вычислить приближенно с помощью дифференциала:

Решение.
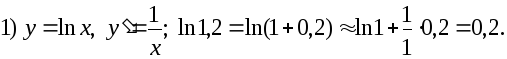
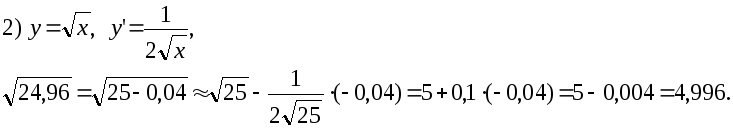
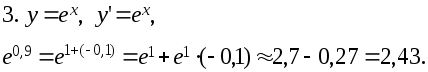
2.29. Найти дифференциал функции и вычислить его значение
при заданных x и
 х:
х: 2)
2)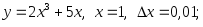
3)
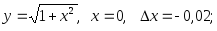 4)
4)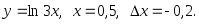
2.30. Вычислить приближенно:
1)
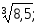 2)
2)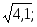 3)
3)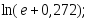 4)
4)
Контрольные задания
Вариант 1.
1. Найти производные функций:
а)
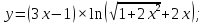
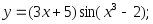 б)
б)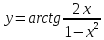
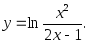
2. Найти производную функции, заданной параметрически:
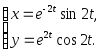
3. Найти производную 2-го порядка:
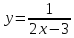
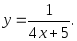
4. Найти Δy и dy функции

 приx
= 2, Δx
= 0,01.
приx
= 2, Δx
= 0,01.5. Вычислить приближенно с помощью дифференциала
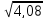
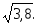
Вариант 2.
1. Найти производные функций:
а)
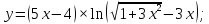
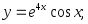 б)
б)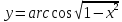
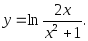
2. Найти производную функции, заданной параметрически:
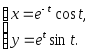
3. Найти производную 2-го порядка:
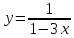
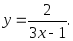
4. Найти Δy и dy функции

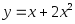 приx
= 3, Δx
= 0,02.
приx
= 3, Δx
= 0,02.5. Вычислить приближенно с помощью дифференциала

Вариант 3.
1. Найти производные функций:
а)
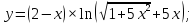
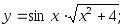 б)
б)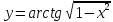
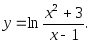
2. Найти производную функции, заданной параметрически:

3. Найти производную 2-го порядка:
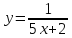

4. Найти Δy и dy функции
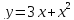
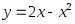 приx
= 1, Δx
= 0,03.
приx
= 1, Δx
= 0,03.5. Вычислить приближенно с помощью дифференциала
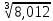
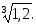
2.4. Приложения производной
Одно из приложений производной − правило Лопиталя при вычислении пределов (в случаях неопределенностей
 и
и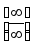 ):
):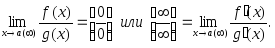
Примеры.
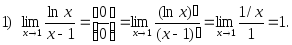
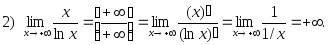

2.31. Найти пределы по правилу Лопиталя:
1)
 ;
2)
;
2)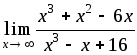 ;
3)
;
3)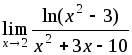 ;
4)
;
4)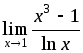 ;
;5)
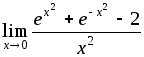 ;
6)
;
6) ;
7)
;
7) ;
8)
;
8)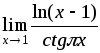 ;
;9)
 ;
10)
;
10)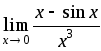 .
.2.4.1. Исследование функции на монотонность,
Экстремумы и выпуклость.
Асимптоты графика функции
Определение. Критической точкой функции у = f(х) называется точка
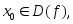 в которой производная равна нулю или
не существует.
в которой производная равна нулю или
не существует.Теорема. Если в промежутке (а; b) производная
 положительна/отрицательна,
то в этом промежутке функция
положительна/отрицательна,
то в этом промежутке функция возрастает/убывает.
возрастает/убывает.Теорема. Если при переходе через критическую точку
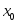 производная
производная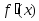 меняет
знак с «+» на «−»
(с «−»
на «+»), то
меняет
знак с «+» на «−»
(с «−»
на «+»), то
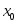 −
точка максимума
(минимума) функции
−
точка максимума
(минимума) функции
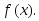
Определение. Функция
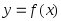 называетсявыпуклой
вверх
(вниз)
в промежутке (а; b),
если в этом промежутке точки графика
лежат под (над) касательными, построенными
в этих точках. Точкой
перегиба
называется точка графика функции,
которая делит его на части с разными
направлениями выпуклости.
называетсявыпуклой
вверх
(вниз)
в промежутке (а; b),
если в этом промежутке точки графика
лежат под (над) касательными, построенными
в этих точках. Точкой
перегиба
называется точка графика функции,
которая делит его на части с разными
направлениями выпуклости.Пример 2.3.
Исследовать функцию
 на монотонность и экстремумы, выпуклость.
на монотонность и экстремумы, выпуклость.Решение.
Исследуем функцию на монотонность и экстремумы.


Сделаем рисунок (рис. 2.1).

Рис. 2.1. Исследование функции на монотонность и экстремумы
х = 1,5 – точка минимума, ymin =
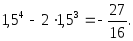
Исследуем функцию на выпуклость.
