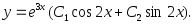- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
Определение. Областью определения функции
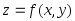 называется
множество точек
называется
множество точек
 плоскостиОху,
в которых функция определена.
плоскостиОху,
в которых функция определена.Линия уровня функции
 задается уравнением z
= C
или
задается уравнением z
= C
или
 .
.Пример 2.7.
Найти область определения функции:
1.
 2.
2.

Решение.
1. Область определения задается условием: 9 – x2 – y2 > 0 или x2 + y2 < 9, т. е. представляет собой незамкнутый круг с центром в начале координат радиуса 3.
2. Имеем: x – y ≥ 0 или y ≤ x, т. е. область определения – это полуплоскость, лежащая ниже прямой y = x, и сама прямая.
2.66. Построить область определения функции:




2.67. Найти линии уровня функций:


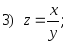

2.7.1. Частные производные, дифференциал,
Градиент функции
Определение. Частные производные функции z = z(x, y):

если пределы существуют.
Определение. Дифференциалом функции z = z(x, y) называется выражение

Определение. Градиентом функции z = z(x, y) называется вектор

Пример 2.8.
Найти частные производные
 и
и (или
(или и
и )
функции
)
функции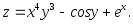
Решение.


2.68. Найти
 и
и :
:1)
 2)
2)
3)
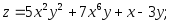 4)
4)
5)
 6)
6)
7)
 8)
8)
9)
 10)
10)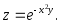
2.69. Найти дифференциал функции z в точке М(–2; 1):
1)
 если
если
2)
 если
если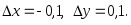
2.70. Найти градиент и линию уровня функции в точке Р, сделать рисунок:
1)
 2)
2)
3)
 4)
4)
2.71. Найти модуль градиента функции:
1)
 в
точкеА(1;
–2; 0);
в
точкеА(1;
–2; 0);2)
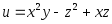 в точкеА(0;
1; –2).
в точкеА(0;
1; –2).2.7.2. Частные производные 2-го порядка.
Исследование функции на экстремум
Пример 2.9.
Найти частные производные второго порядка функции z = x2y3+2y.
Решение.
 =
=
 =
= =2y3
=2y3
 =
2y3,
=
2y3,
 =
= =
= =2х
=2х
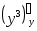 =
6xy2,
=
6xy2, =
= =
= =3y2
=3y2
 =
6xy2,
=
6xy2,
 =
= =
= =
3х2
=
3х2
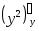 =
6x2y.
=
6x2y.2.72. Найти частные производные второго порядка
 :
:1)
 2)
2)
3)
 4)
4)
2.73. Доказать, что если
 то
то
Схема исследования функции z = z(x, y) на экстремум:
1. Найти частные производные
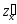 ,
,
 и
решить систему уравнений
и
решить систему уравнений
Решениями системы будут критические точкифункции.
2. Найти частные производные 2-го порядка.
3. Для каждой критической точки вычислить определитель

Если ∆ > 0, то критическая точка является точкой максимума/минимума функции при условии
 <
0/
<
0/ > 0.
> 0.Если ∆ < 0, то критическая точка не является точкой экстремума.
Если ∆ = 0, то требуется дополнительное исследование (изучается вопрос о знакопостоянстве функции в окрестности критической точки).
4. Вычислить экстремумы функции, подставив координаты точек экстремумов в уравнение z=z(x,y).
Пример 2.10.
Производятся два вида товаров, в количествах х ед. и y ед. Пусть 8 и 10 ден. ед. – цены на эти товары соответственно, а S = x2 + xy + y2 – функция затрат. Определить оптимальный выпуск товаров, при котором предприятие получит максимальную прибыль.
Решение.
Функция прибыли имеет вид:
П(х, y) = 8х + 10y – x2 – xy – y2.
Вычислим частные производные первого порядка:
Пх΄ = 8 – 2х – y, Пy΄ = 10 – х – 2y.
Найдем критические точки функции как решение системы уравнений

получаем точку (2; 4).
Найдем частные производные второго порядка:
 = –2,
= –2,
 =
= = –1,
= –1,
 = –2.
= –2.Так как
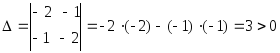 и
и = –2 <
0, то в точке
(2; 4)
функция прибыли имеет максимум: Пmax
= П (2; 4) =
28.
= –2 <
0, то в точке
(2; 4)
функция прибыли имеет максимум: Пmax
= П (2; 4) =
28.Следовательно, для получения максимальной прибыли в 28 денежных единиц необходимо произвести 2 ед. товара первого вида и 4 ед. – второго вида.
2.74. Исследовать функцию на экстремумы:
1)
 2)
2)
3)
 4)
4)
5)
 6)
6)
2.75. Производственная функция (в ден. ед.) имеет вид
 гдех
и у
– количество ед. соответственно 1-го
и 2-го ресурсов. Стоимость ед. первого
ресурса – 5, а второго – 10 (ден. ед.).
Найти максимальную прибыль при
использовании этих ресурсов.
гдех
и у
– количество ед. соответственно 1-го
и 2-го ресурсов. Стоимость ед. первого
ресурса – 5, а второго – 10 (ден. ед.).
Найти максимальную прибыль при
использовании этих ресурсов.2.76. Как распределить сумму в $10 млн между тремя компаниями так, чтобы их суммарная прибыль была наибольшей, если прибыль каждой определяется соответственно по формуле:


 где
где –
инвестируемая сумма?
–
инвестируемая сумма?2.77. Исследовать функцию на экстремумы и найти наименьшее и наибольшее значения в заданной области:
1)

 АВО:
А(–5;
0), В(0; –5),
О(0; 0);
АВО:
А(–5;
0), В(0; –5),
О(0; 0);2)
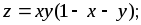
 АВС:
А(2; 0), В(0; 2), С(0;
–2).
АВС:
А(2; 0), В(0; 2), С(0;
–2).2.78. Из всех прямоугольных параллелепипедов, имеющих данную сумму длин ребер а, найти параллелепипед, имеющий наибольший объем.
2.7.3. Метод наименьших квадратов
Пусть дана таблица значений функции
xi x1 x2 … xп
yi y1 y2 … yп.
Параметры а и b линейной функции
 которая аппроксимирует данную
зависимость, находят как решение
системы
которая аппроксимирует данную
зависимость, находят как решение
системы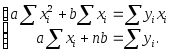
2.79. Имеются следующие данные о величине пробега автомобиля х (тыс. км) и расходе у (л/тыс. км):
xi 50 70 90 110 130
yi 0,2 0,5 0,8 1,1 1,3.
Полагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу
 методом наименьших квадратов.
методом наименьших квадратов.2.80. Имеются следующие данные:
xi 3 4 5 6 7
yi 200 160 120 90 80,
где х – цена на товар (ден. ед.);
у – уровень продаж (тыс. ед.).
Полагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу
 методом наименьших квадратов.
методом наименьших квадратов.Контрольные задания
1. Найти частные производные 1-го порядка:
1)
 2)
2) 3)
3)
2. Найти экстремумы функции:
1)
 2)
2) 3)
3)
3. Предполагая, что между переменными х и у существует линейная зависимость, найти эмпирическую формулу
 методом наименьших квадратов по
следующим данным:
методом наименьших квадратов по
следующим данным:1) xi 1 2 3 4
yi 1,3 2 2,5 2,8;
2) xi 1 2 3 4
yi 4 3 1 0;
3) xi 1 2 3 4
yi 3 3,4 3,6 4.
2.8. Дифференциальные уравнения
Определение. Дифференциальным уравнением называется соотношение, связывающее независимую переменную, искомую функцию и её производные или её дифференциалы. В случае, когда неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, дифференциальное уравнение называется обыкновенным.
Рассмотрим некоторые типы дифференциальных уравнений.
1. Уравнение с разделяющимися переменными
у'=f1(x)f2(y).
Решение.
dy/dx = f1(x)f2(y) | dx/ f2(y), f2(y) ≠ 0,
dy/ f2(y) = f1(x) dx,
 общее
решение (общий интеграл) уравнения.
общее
решение (общий интеграл) уравнения.Случай f2(y)= 0 рассматривается с помощью подстановки в исходное уравнение.
Пример 2.11. Решить уравнение

Решение.
dy/dx = у2сosx | dx/у2, у ≠ 0,
dy/у2 = cosxdx,

–1/y = sinx + C,
y = –1/(sinx + C) – общее решение.
Рассмотрим случай у = 0.
Подставляя в исходное уравнение у = 0, получаем:
0' = 02cosx, 0 = 0 – верно у = 0 – решение уравнения.
Это решение не может быть получено как частное решение общего решения ни при каком значении С.
Ответ: y = –1/(sinx + C), у = 0.
2.81. Решить уравнения:
1)
 2)
2) 3)
3)
4)
 5)
5) 6)
6)
7)
 8)
8)
2. Однородные уравнения 1-го порядка

Уравнения решают с помощью замены

После подстановки z и
 в исходное уравнение получается
уравнение с разделяющимися переменными
(см. п. 1).
в исходное уравнение получается
уравнение с разделяющимися переменными
(см. п. 1).2.82. Решить уравнения:
1)
 2)
2) 3)
3)
4)
 5)
5)
6)

3. Линейные уравнения 1-го порядка
у' +p(x)y =f(x),
где p(x),f(x) – непрерывные функции.
Пример 2.12. Решить уравнение у' + xy = x.
Решение.
Пусть
 тогда
тогда и уравнение принимает вид
и уравнение принимает вид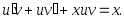
Группируя первое и третье слагаемые, получаем

Равенство будет верным, если

Найдем частное решение первого уравнения системы:

Подставим полученное решение во второе уравнение системы и найдем его общее решение:

C помощью замены
 получаем общее решение:
получаем общее решение:
Подставляя найденные решения
 и
и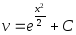 в равенство
в равенство получаем решение исходного уравнения:
получаем решение исходного уравнения:
Ответ:

Задача Коши для уравнения 1-го порядка имеет вид

Пример 2.13.
Решить задачу Коши

Решение.
Найдем общее решение уравнения
 :
:dy/dx = х2у | dx/у, у ≠ 0,
dy/у = x2 dx,

ln|y| = х3 /3 + С.
Подставим в это решение х = 2 и у = 1 (см. условие у(2) = 1):
ln|1| = 23 /3 + С,
0 = 8/3 + С С = – 8/3.
Подставляя это значение в общее решение, получаем
Ответ: ln|y| = (х3 – 8)/3.
2.83. Решить уравнение или задачу Коши:
1)
 2)
2)
3)
 4)
4)
5)
 6)
6)
7)
 8)
8)
4. Линейные однородные уравнения 2-го порядка
С постоянными коэффициентами
 ,
,
где p, q
 R.
R.Решение.
Составим характеристическое уравнение
 и решим его.
и решим его.Возможны три случая:
k1,2
 R,
k1
≠ k2
(дискриминант D
> 0);
R,
k1
≠ k2
(дискриминант D
> 0);k1,2
 R,
k1
= k2
= k
(D = 0);
R,
k1
= k2
= k
(D = 0);k1,2 =

 C
(D < 0).
C
(D < 0).
Каждому из этих случаев соответствует общее решение уравнения:
Пример 2.14.
Решить уравнения:
Решение.

 Ответ:
Ответ:

 Ответ:
Ответ:


 Ответ:
Ответ: