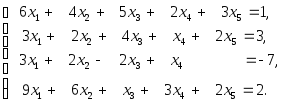- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
Системы линейных уравнений
Рассмотрим три основных метода решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Заметим, что метод Крамера и матричный могут применяться только для невырожденных систем, т. е. систем с определителем, неравным нулю. При этом система имеет единственное решение. Метод Гаусса более универсальный и позволяет решать как определенные системы (имеющие единственное решение), так и неопределенные системы, имеющие множество решений. Применяя преобразования метода Гаусса, можно ответить на вопрос: совместна ли система или вообще не имеет решений, найти ранг матрицы.
Пример 1.6. Решение системы методом Крамера.
Решить
систему
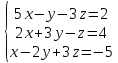 .
.
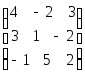
Строим матрицу системы, вычисляем её определитель:
∆ =
 = 45 + 1 + 12 – (–9 + (–6) + 10) = 63.
= 45 + 1 + 12 – (–9 + (–6) + 10) = 63.
Построим
определитель![]() ∆1
заменой
1-го столбца на столбец правых частей и
вычислим:
∆1
заменой
1-го столбца на столбец правых частей и
вычислим:
∆1
=
 = 18 + (–5) + 24 – (45 + (–12) + 4) = 0,
тогда
переменная х находится по формуле х
=
= 18 + (–5) + 24 – (45 + (–12) + 4) = 0,
тогда
переменная х находится по формуле х
=
![]() =
=
![]() = 0.
= 0.
Найдем ∆2 заменой 2-го столбца на столбец правых частей:
∆2= = 60 + (–2) + 30 – (– 12 + 12 + 25) = 63,
= 60 + (–2) + 30 – (– 12 + 12 + 25) = 63,
тогда
переменная y
находится по формуле y
=
![]() = 1.
= 1.
Найдем ∆3 заменой 3-го столбца на столбец правых частей:
∆3= =
– 75 + (–4) + (–8) – (6 +10 + (–40)) = –63,
=
– 75 + (–4) + (–8) – (6 +10 + (–40)) = –63,
тогда
переменная z
находится по формуле z
=
![]() = –1.
= –1.
Ответ: (x, y, z) = (0, 1, –1).
Пример 1.7. Решение системы методом Гаусса.
Построим
по данной системе расширенную
матрицу системы
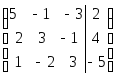 .
.
Её
необходимо с помощью элементарных
преобразований привести к треугольному
виду
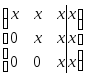 .
Ниже главной диагонали должны быть
нули.
.
Ниже главной диагонали должны быть
нули.
Разрешены следующие элементарные преобразования, не меняющие пространства решений системы:
можно менять местами строки;
умножать строку на ненулевое число;
складывать или вычитать любые две строки, умноженные на любое число;
вычеркивать нулевые или пропорциональные строки.
Если в столбце есть 1, удобно переставить строки, поставив 1 на первое место. Умножим первую на 2, вычтем из второй:
![]()
![]()
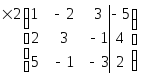 ~
~
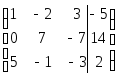 .
.
Разделим 2-ю строку на 7, переставим с 3-й, первую умножим на 5, вычтем из второй, получаем:
![]()
![]()
![]()
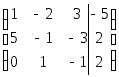
![]() ~
~
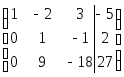 .
.
Разделим
3-ю строку на 9 и вычтем 2-ю, имеем
![]()
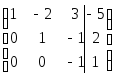 .
Эта матрица приведена к треугольному
виду. Первый этап закончен.
.
Эта матрица приведена к треугольному
виду. Первый этап закончен.
Построим
теперь по ней систему уравнений:
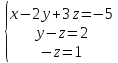 .
.
Приступаем ко второму этапу – обратный ход метода Гаусса. Находим из последнего уравнения z = –1; поднимаясь во второе и подставляя найденное z, находим y = 1; затем из первого находим х = 0. Итак, (x, y, z) = (0, 1, –1).
1.9. Определить ранг матрицы В (табл. 1.5).
Таблица 1.5
|
№ |
1 |
2 |
3 |
4 |
|
Матрица В |
2 5 6 4 –1 5 2 –6 –1 |
1 2 1 4 0 5–1 4 –1 3 4 6 |
1 3 7 2 5 –1 0 4 8 3 3 6 10 –4 7 |
2 0 3 5 1 4 3 1 7 5 0 3 –5 –3 3 2 3 –2 2 4 |
Замечание. Для вычисления ранга матрицы удобно привести ее к треугольному виду с помощью элементарных преобразований. Количество ненулевых строк, оставшихся после приведения, равно рангу матрицы.
1.10. Решить систему уравнений различными методами. В таблице 1.6 указаны матрица системы А и столбец правых частей В.
Таблица 1.6
|
№ |
А |
В |
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
7 |
|
|
|
8 |
|
|
1.11. Исследовать систему на совместность и в случае совместности методом Гаусса найти общее решение, указать хотя бы одно базисное решение:
1)
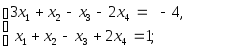 2)
2)
3)
 4)
4)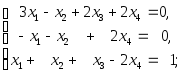
5)
 6)
6)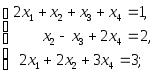
7)
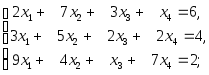 8)
8)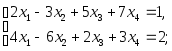
9)
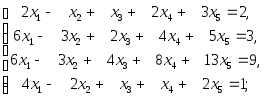
10)