
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
а) выпадение числа 7 на верхней грани игральной кости при ее однократном бросании;
б) выпадение натурального числа, лежащего в пределах от 1 до 6, на верхней грани игральной кости при ее однократном бросании;
г) выпадение орла и решки при однократном бросании монеты.
3.25. Какие из перечисленных событий являются несовместными, а какие независимыми:
а) событие A − выпадение на верхней грани игральной кости четного числа и событие B − выпадение на верхней грани игральной кости нечетного числа;
б) событие C − попадание в цель стрелком при первом выстреле и событие D − попадание в цель стрелком при втором выстреле;
г) событие E − выпадение орла при бросании первой монеты и событие F − выпадение орла при бросании второй монеты;
д) событие H1 – вытащить случайным образом белый шар из урны, содержащей 5 белых, 3 красных и 7 черных шаров, событие H2 − красный шар, событие H3 – черный шар.
3.26. Какие события являются противоположными следующим событиям:
а) выпадение четного числа на верхней грани игральной кости;
б) выпадение на верхней грани игральной кости числа меньше четырех;
в) попадание стрелком в цель;
г) выпадение орла при бросании монеты;
д) из колоды карт вытащить наугад карту красной масти;
е) из колоды карт вытащить наугад карту бубновой масти.
3.2.3. Алгебра событий
Определение. Суммой событий A и B (A + B) называется такое событие C, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий A или B.
Разъяснить смысл операции суммы событий можно с помощью таблицы 3.1, в которой знак «+» обозначает наступление события, а «−» соответствует ситуации, когда событие не наступило.
Таблица 3.1
Сумма событий A и B
A
B
A+B
+
+
+
+
−
+
−
+
+
−
−
−
Операция суммы событий аналогична операциям объединения множеств и дизъюнкции.
Замечание. Операции суммы событий, как и операции объединения множеств, соответствует союз русского языка «или».
С помощью метода математической индукции операция суммы распространяется на любое число событий.
Определение. Суммой событий A1, A2, A3, … , An называется такое событие C, которое происходит тогда и только тогда, когда происходит хотя бы одно из событий A1, или, A2, или, A3, или, …, или An.
Пример 3.12. Пусть событие A – попадание в цель первым стрелком, событие B – попадание в цель вторым стрелком. Что представляет собой событие, являющееся суммой этих событий? Что представляет собой событие, противоположное сумме событий A и B?
Суммой событий A и B является событие C, состоящее в попадании в цель хотя бы одним стрелком, т. е. событие C произойдет, если первый стрелок попадет в цель, а второй – не попадет в цель или второй стрелок попадет в цель, а первый – не попадет в цель или оба стрелка попадут в цель.
Событие, противоположное сумме событий A и B, произойдет тогда и только тогда, когда оба стрелка не попадут в цель, т. е. и первый стрелок не попадет в цель и второй стрелок не попадет в цель.
Пример 3.13. Пусть событие A – выпадение двойки на верхней грани игральной кости, событие B – выпадение четверки, C – выпадение шестерки. Что представляет собой событие, являющееся суммой этих событий? Что представляет собой событие, противоположное сумме событий A, B и C?
Суммой событий A, B и C является событие, состоящее в выпадении четного числа на верхней грани игральной кости.
Событие, противоположное сумме событий A, B и C, состоит в выпадении нечетного числа (единицы, или тройки, или пятерки) на верхней грани игральной кости.
Пример 3.14. Рассмотрим опыт с бросанием двух монет. Пусть событие A – выпадение орла и на первой монете и на второй монетах, событие B – выпадение решки на первой монете и орла на второй монете, C – выпадение орла на первой монете и решки на второй монете, D – выпадение решки и на первой и на второй монетах. Что представляет собой событие, состоящее в выпадении хотя бы одного орла?
Событие, состоящее в выпадении хотя бы одного орла, представляет собой сумму событий A, B и C, т. е. A + B + C.
Определение. Произведением событий A и B (A × B) называется такое событие C, которое происходит тогда и только тогда, когда происходят оба события A и B.
Разъяснить смысл операции произведения событий можно с помощью таблицы 3.2, в которой знак «+» обозначает наступление события, а «−» соответствует ситуации, когда событие не наступило.
Таблица 3.2
Произведение событий A и B
A
B
A× B
+
+
+
+
−
−
−
+
−
−
−
−
Операция произведения событий аналогична операциям пересечения множеств и конъюнкции.
Замечание. Операции произведения событий, как и операции пересечения множеств, соответствует союз русского языка «и».
С помощью метода математической индукции операция произведения распространяется на любое число событий.
Определение. Произведением событий A1, A2, A3, … , An называется такое событие C, которое происходит тогда и только тогда, когда происходят все события A1, и A2, и A3, и …, и An.
Пример 3.15. Пусть событие A – попадание в цель первым стрелком, событие B – попадание в цель вторым стрелком. Что представляет собой событие, являющееся произведением событий A и B? Что представляет собой событие, противоположное произведению событий A и B?
Произведением событий A и B является событие C, которое происходит тогда и только тогда, когда оба стрелка попадают в цель, т. е. и первый стрелок и второй стрелок попадут в цель.
Событие, противоположное произведению событий A и B, произойдет тогда и только тогда, когда хотя бы один стрелок не попадет в цель, т. е. событие
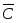 произойдет, если первый стрелок попадет
в цель, а второй–
не попадет в цель или второй стрелок
попадет в цель, а первый –
не попадет в цель или оба стрелка не
попадут в цель.
произойдет, если первый стрелок попадет
в цель, а второй–
не попадет в цель или второй стрелок
попадет в цель, а первый –
не попадет в цель или оба стрелка не
попадут в цель.3.2.4. Статистический подход к понятию вероятности
Определение. Относительной частотой события A называется отношение числа испытаний N(A), в которых это событие произошло к полному числу испытаний в серии N, т. е.
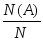 при этомN(A)£
N.
при этомN(A)£
N.
Пример 3.16. В серии испытаний, состоящей из 1000 бросаний монеты, орел выпал 508 раз, тогда относительная частота выпадения орла равна 0,508.
Результаты наблюдений показывают, что при достаточно большом числе испытаний частота появления события обладает свойством устойчивости.
Рассмотрим различные серии испытаний, связанных с бросанием симметричной монеты и представим их результаты в виде таблицы 3.3.
Заметим, что многие ученые проводили подобный эксперимент. Данные серий 5, 6, 7, 8, 9 и 10, представленные в таблице 3.3, соответствуют реальным результатам, полученным Бюффоном, Де Морганом, Джевонсом и Романовским, Пирсоном и Феллером.
Результаты 5–10 серий позволяют сделать вывод об устойчивости частоты появления события при достаточно большом числе испытаний в серии. В нашем случае частота выпадения орла близка к 0,5.
Таблица 3.3
Результаты серий испытаний
№ серии
Число бросков
Частота выпадения орла
1
2
0
2
3
1
3
5
0, 2
4
6
0,66
5
4040
0,507
6
4092
0,5005
7
20 480
0,506 8
8
80 640
0,4923
9
24 000
0,5005
10
10 000
0,4979
В настоящее время все чаще вместо натурного эксперимента используют компьютерный эксперимент, в котором моделируются реальные испытания, например, бросания монеты или игральной кости.
Определение. Вероятностью события А называется число, к которому стремится относительная частота этого события при неограниченном увеличении количества испытаний в серии.
Вероятность события A принято обозначать P(A).
Следовательно, можно записать формулу для нахождения вероятности следующим образом:
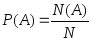 при
при
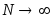 .
(3.7)
.
(3.7)Замечание. Значения вероятности всегда лежат в пределах от нуля до единицы включительно:
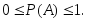
Действительно, статистическая вероятность оценивается относительной частотой появления события при большом числе испытаний
 ,
гдеN
– число
испытаний
в серии и выражается натуральным
числом, N(A)
–
число
испытаний
в которых событие A
произошло,
является либо натуральным числом, либо
нулем. Минимальное значение, которое
может принимать отношение
,
гдеN
– число
испытаний
в серии и выражается натуральным
числом, N(A)
–
число
испытаний
в которых событие A
произошло,
является либо натуральным числом, либо
нулем. Минимальное значение, которое
может принимать отношение
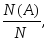 равно нулю при условии, что событиеA
ни разу не
произойдет, максимальное –
единице при условии, что событие A
происходит
в каждом испытании серии.
равно нулю при условии, что событиеA
ни разу не
произойдет, максимальное –
единице при условии, что событие A
происходит
в каждом испытании серии.Статистический поход к определению понятия вероятности широко используется на практике, например, при проведении социологических, экономических и других исследований.
Пример 3.17. Известно, что в партии из 1000 деталей отдел технического контроля обнаружил 50 нестандартных деталей. Оценить вероятность обнаружения бракованной детали.
По условию задачи число испытаний в серии N=1000 является достаточно большим, поэтому вероятность события A (обнаружение бракованной детали в партии) можно оценить с помощью относительной частоты этого события. Учитывая статистический подход к понятию вероятности и используя формулу (3.7), имеем:
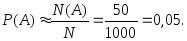
3.2.5. Классический подход к понятию вероятности
В классическом походе к определению понятия вероятности рассматриваются частные случаи, в которых можно определить вероятность события без проведения большой серии испытаний. Этот подход предложен французским математиком П. Лапласом (1749−1817 гг.) и применим он только для моделей случайных событий с равновозможными исходами. Например, при рассмотрении опытов с бросанием игральной кости или монеты подразумевается, что они идеально симметричны, изготовлены из однородного материала, никогда не станут на ребро и не укатятся из поля зрения наблюдателя.
Определение. Событие В называется благоприятствующим событию A, если его наступление в результате испытания всегда приводит к наступлению события A.
Пример 3.18. Рассмотрим опыт с бросанием игральной кости. Пусть событие B – выпадение двойки на верхней грани игральной кости, а событие A – выпадение четного числа. Реализация в результате испытания события B всякий раз влечет за собой наступление события A, следовательно, событие B является благоприятствующим событию A.
Пример 3.19. Рассмотрим опыт, связанный с бросанием игральной кости, имеющий конечное число равновозможных, образующих полную группу исходов. В данном опыте возможны следующие исходы: U1 – выпадение на верхней грани единицы, U2 – двойки, U3 – тройки, … , U6 – шестерки. Действительно, события U1, U2, … , U6 – попарно несовместны, т. к. в результате каждого испытания обязательно произойдет одно и только одно из этих событий.
При выполнении условия идеальной симметричности игральной кости (никакая из граней не утяжелена, грани кубика одинаковые и пр.) события U1, U2, … , U6 в длинной серии испытаний реализуются с одинаковой частотой, т. е. являются равновозможными (равновероятными).
События, обладающие перечисленными свойствами, называются элементарными.
Определение. Элементарными событиями называются попарно несовместные, равновозможные события, образующие полную группу.
Совокупность элементарных событий называется пространством элементарных событий и обозначается Ω.
Пример 3.20. Рассмотрим опыт с бросанием монеты. Какие исходы в рамках данного опыта можно считать элементарными?
Элементарными являются следующие исходы (события): U1 – выпадение орла, U2 – выпадение решки. Действительно, если монета симметрична, то эти исходы являются равновозможными, попарно несовместными и образуют полную группу.
Пример 3.21. Рассмотрим опыт с бросанием двух монет. Какие исходы в рамках данного опыта можно считать элементарными?
С одной стороны, можно считать элементарными события: U1 – выпадение на первой монете орла, U2 – выпадение на первой монете решки, U3 – выпадение на второй монете орла, U4 – выпадение на второй монете решки. Действительно, перечисленные события удовлетворяют определению понятия элементарных событий.
С другой стороны, можно считать элементарными следующие события: H1 – выпадение орла и на первой и на второй монетах, H2 – выпадение решки и на первой и на второй монетах, H3 – выпадение на первой монете решки, а на второй монете – орла, H4 – выпадение на первой монете орла, а на второй монете – решки. События H1, H2, H3 и H4 также удовлетворяют определению понятия элементарных событий.
Необходимо отметить, что события U1, U2, U3, U4 и H1, H2, H3, H4 связаны между собой следующим образом:
H1 =U1× U3, H2 =U2 × U4, H3 =U2 × U3, H4 =U1 × U4.
Вывод. Оптимальный выбор элементарных событий часто значительно упрощает решение задачи.
Определение. Вероятностью события A называется отношение числа исходов N(A), благоприятствующих событию A, к полному числу элементарных исходов N:
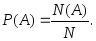 (3.8)
(3.8)Пример 3.22. Рассмотрим опыт с бросанием монеты. Найти вероятность выпадения орла. Обозначим через A событие, связанное с выпадением орла. В рамках условия задачи всего два элементарных исхода: U1 – выпадение орла, U2 – выпадение решки. Из них благоприятным событию A является только одно. С помощью формулы (3.8) найдем вероятность события A:
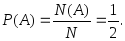
Пример 3.23. Рассмотрим элементарные исходы, связанные с бросанием двух монет: H1 – выпадение орла и на первой и на второй монетах, H2 – выпадение решки и на первой и на второй монетах, H3 – выпадение на первой монете решки, а на второй монете – орла, H4 – выпадение на первой монете орла, а на второй монете – решки. Можно ли считать исходы H3 и H4, связанные с выпадением на одной монете орла, а на другой – решки, в одном испытании? Поставленный вопрос можно сформулировать иначе: сколько существует в рамках этой задачи элементарных исходов 3 или 4?
При классическом подходе к понятию вероятности, когда проводят лишь мысленный эксперимент, ответить на поставленный вопрос невозможно. Однако результаты реальных экспериментов, связанных с достаточно большими сериями испытаний, позволяют утверждать, что при проведении опыта с бросанием более чем одной монеты, более чем одного кубика и пр., монеты, кубики и т. д. различимы. Таким образом, исходы H3 и H4 являются различными исходами, следовательно, в рассматриваемой задаче 4 элементарных исхода. Следовательно, вероятности событий H1 – выпадения орла и на первой и на второй монетах и H2 – выпадение решки и на первой и на второй монетах равны, т. к. только один исход является благоприятствующим этим событиям, а всего элементарных исходов – четыре, используя формулу (3.8), получим:
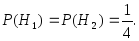
Вероятность события H, связанного с выпадением на одной монете орла, а на другой – решки, т. е. события H = H3 + H4, равна 1/2, т. к. два исхода являются благоприятными этому событию, а всего элементарных исхода – четыре, используя формулу (3.8), получим:
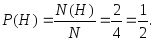
3.26. Рассмотрим опыт с бросанием двух монет. Найти вероятность выпадения:
а) хотя бы одного орла;
б) хотя бы одной решки;
в) не менее одной решки.
3.27. При проведении испытания с бросанием игральной кости найти вероятность выпадения на верхней грани кости:
а) шести очков;
б) пяти очков;
в) менее одного очка;
г) не более двух очков;
д) хотя бы трех очков;
ж) не менее пяти очков.
з) не менее двух и не более пяти очков.
3.2.6. Решение вероятностных задач
С помощью комбинаторики
Комбинаторику используют только для решения вероятностных задач с равновозможными исходами, т. е. в рамках классического подхода к понятию вероятности.
Пример 3.24. В урне 5 белых и 4 черных шара. Найти вероятность события: A – вытащить наугад белый шар, B – вытащить наугад два белых шара, C – вытащить наугад один белый и один черный шар, D – два шара одного цвета.
Число всех элементарных исходов при вытаскивании из урны наугад одного шара равно 9 или
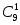 − числу сочетаний из девяти элементов
по одному, т. к. всего шаров в урне 9 и
выбрать один из них можно девятью
способами. Благоприятствующих событиюA
исходов – пять или
− числу сочетаний из девяти элементов
по одному, т. к. всего шаров в урне 9 и
выбрать один из них можно девятью
способами. Благоприятствующих событиюA
исходов – пять или
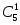 ,
поскольку белый шар можно вытащить из
5 белых шаров, следовательно, имеем:
,
поскольку белый шар можно вытащить из
5 белых шаров, следовательно, имеем:
Число всех элементарных исходов при вытаскивании из урны наугад двух шаров из 9 равно
 − числу сочетаний из девяти элементов
по два. Учитывая, что число благоприятствующих
событиюB
исходов соответственно равно
− числу сочетаний из девяти элементов
по два. Учитывая, что число благоприятствующих
событиюB
исходов соответственно равно
 ,
получим:
,
получим: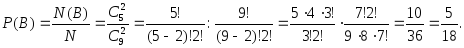
При нахождении вероятности события C – вытащить наугад один белый и один черный шар, число всех элементарных исходов также равно
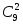 .
Число благоприятствующих событиюC
исходов найдем используя правило
произведения комбинаторики. Множество
белых шаров содержит пять элементов,
а множество черных – четыре, тогда
число пар, образованных из элементов
этих множеств, равно произведению
количества элементов в этих множествах,
т. е.
.
Число благоприятствующих событиюC
исходов найдем используя правило
произведения комбинаторики. Множество
белых шаров содержит пять элементов,
а множество черных – четыре, тогда
число пар, образованных из элементов
этих множеств, равно произведению
количества элементов в этих множествах,
т. е.
 Тогда вероятность событияC
равна:
Тогда вероятность событияC
равна: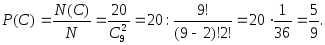
Теперь найдем вероятность события D – вытащить два шара одного цвета, которое состоит в выборе наугад двух белых или двух черных шаров. Число всех элементарных исходов по прежнему равно
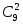 .
Используя правило суммы комбинаторики,
получим, что число благоприятствующих
событиюD
исходов равно
.
Используя правило суммы комбинаторики,
получим, что число благоприятствующих
событиюD
исходов равно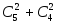 ,
т. к. число способов выбора двух элементов
из множества, содержащего пять элементов
или из множества, содержащего четыре
элемента (множества не пересекаются),
равно сумме числа способов выбора двух
элементов из каждого множества. Число
всех элементарных исходов по прежнему
равно
,
т. к. число способов выбора двух элементов
из множества, содержащего пять элементов
или из множества, содержащего четыре
элемента (множества не пересекаются),
равно сумме числа способов выбора двух
элементов из каждого множества. Число
всех элементарных исходов по прежнему
равно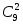 .
Учитывая вышеизложенное, получим:
.
Учитывая вышеизложенное, получим: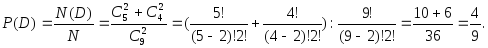
Пример 3.25. В опыте с бросанием двух игральных костей найти вероятности выпадений в сумме на верхних гранях U2 – двух очков, U3 – трех очков, U4 – четырех очков, …, U12 – двенадцати очков.
Используя правило произведения комбинаторики, найдем число всех элементарных исходов, учитывая, что множество исходов при бросании первой кости содержит шесть элементов и множество исходов при бросании второй кости также содержит шесть элементов. Тогда число пар, образованных из элементов этих множеств, равно произведению количества элементов этих множеств, т. е.
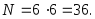
Учитывая, что событиям U2 и U12 благоприятны по одному исходу – выпадение единиц на двух костях и соответственно выпадение шестерок на двух костях, найдем вероятности этих событий:
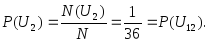
Событию U3 благоприятны два исхода: выпадение на первой кости единицы и на второй – двойки или выпадение на первой кости двойки и на второй – единицы, так как известно (3.8.), что при бросании двух и более костей (монет) они всегда считаются различимыми. Учитывая, что событию U11 также благоприятны два исхода: выпадение на первой кости пятерки и на второй – шестерки или наоборот, получим:
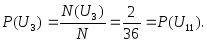
Событию U4 благоприятны три исхода: выпадение на первой кости единицы и на второй – тройки или выпадение на первой кости тройки и на второй – единицы или выпадение двух очков и на первой и на второй костях. Заметим, что событию U10 также благоприятны три исхода: выпадение на первой кости шестерки и на второй – четверки или выпадение на первой кости четверки и на второй – шестерки или выпадение пяти очков и на первой и на второй костях, следовательно, имеем:

Рассуждая аналогичным образом, получим:

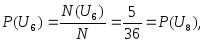
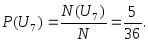
Заметим, что событие, связанное с выпадением в сумме на верхних гранях двух игральных костей числа очков не менее двух и не более двенадцати является достоверным и его вероятность равна единице. Поскольку в каждом испытании одно из событий, состоящих в выпадении от двух до двенадцати очков включительно, обязательно произойдет, а суммарная вероятность рассматриваемых событий равна единице.
Для большей наглядности, представим полученные результаты в виде таблицы 3.4:
Таблица 3.4
Распределение очков в опыте
с бросанием двух игральных костей
Число очков
2
3
4
5
6
7
8
9
10
11
12
3.28. В опыте с бросанием двух игральных костей найти вероятность выпадения в сумме на верхних гранях:
а) менее трех очков;
б) более девяти очков;
в) более четырех и менее десяти;
г) хотя бы девяти очков.
Числа от 1 до 100 записывают на отдельных одинаковых карточках, помещают их в вазу и тщательно перемешивают. После этого наугад извлекают одну карточку. Найти вероятность события:
