
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
Вариант 3.
1. Найти

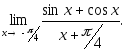
2. Исследовать функцию и построить ее график:

2.5. Неопределенный интеграл
Определение. Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех х из этого промежутка выполняется равенство F′(x) = f(x).
Определение. Неопределенным интегралом от функции f(x) называется семейство ее первообразных:
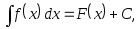
где F(x) – некоторая первообразная для f(x);
C – произвольная постоянная.
Основные свойства неопределенного интеграла
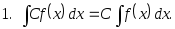
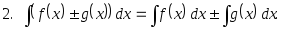

Таблица интегралов
1.
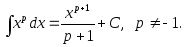
2.

3.
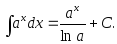 Частный случай:
Частный случай: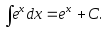
4.
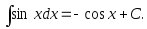
5.
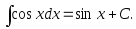
6.
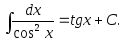
7.
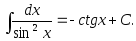
8.

Частный случай:


9.

Частный случай
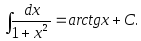
10.
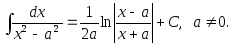
11.
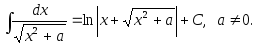
Примеры.
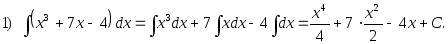


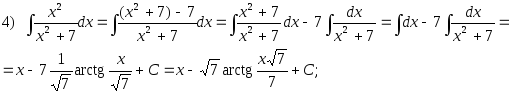

2.50. Найти интегралы:
1)
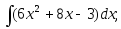 2)
2)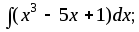 3)
3)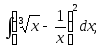
4)
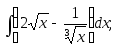 5)
5)
6)
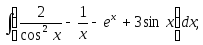
7)
 ;
8)
;
8) ;
9)
;
9)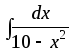 ;
10)
;
10)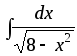 ;
;11)
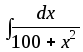 ;
12)
;
12)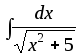 ;
13)
;
13) ;
14)
;
14)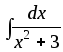 .
.2.51. Найти интегралы:
1)
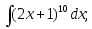 2)
2)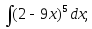 3)
3)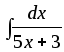 ;
4)
;
4)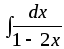 ;
;5)
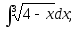 6)
6)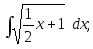 7)
7) 8)
8)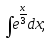
9)
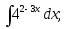 10)
10)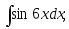 11)
11)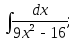 12)
12)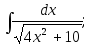
13)
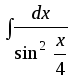 ;
14)
;
14)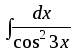 ;
15)
;
15)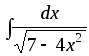 ;
16)
;
16)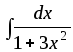 ;
;17)
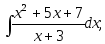 18)
18)
2.5.1. Метод замены переменной
в неопределенном интеграле
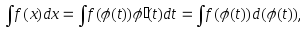
где
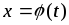 – дифференцируемая функция.
– дифференцируемая функция.Примеры.
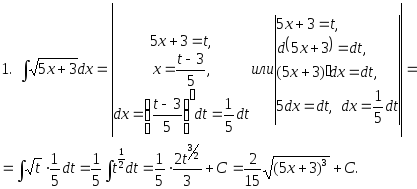
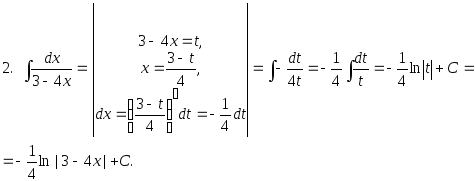

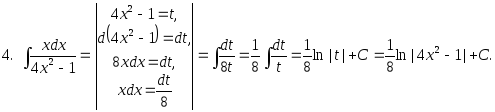
2.52. Найти интегралы методом замены переменной:
1)
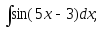 2)
2) 3)
3)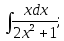
4)
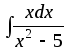 ;
5)
;
5)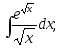 6)
6)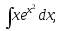
7)
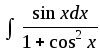 ;
8)
;
8)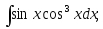 9)
9)
10)
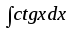 ;
11)
;
11)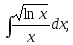 12)
12)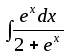 ;
;13)
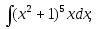 14)
14) 15)
15) ;
;16)
 ;
17)
;
17)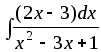 ;
18)
;
18)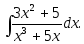
Пример 2.4.
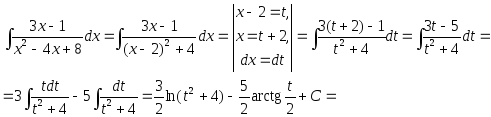
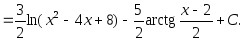
2.53. Найти интегралы от рациональных функций.
1)
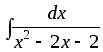 ;
2)
;
2)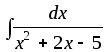 ;
3)
;
3)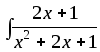 dx;
dx;4)
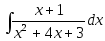 ;
5)
;
5)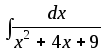 ;
6)
;
6) ;
;7)
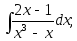 8)
8)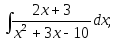 9)
9) dx;
dx;10)
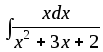 ;
11)
;
11)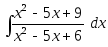 ;
12)
;
12)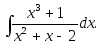
Пример 2.5.

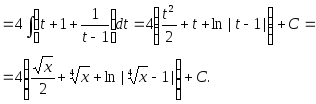
2.54. Найти интегралы от иррациональных функций:
1)
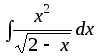 ;
2)
;
2)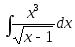 ;
3)
;
3)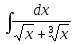 ;
4)
;
4)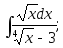
5)
 6)
6) ;
7)
;
7)
2.55. Найти интегралы от тригонометрических функций:
1)
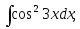 2)
2)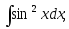 3)
3) 4)
4)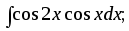
5)
 ;
6)
;
6)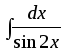 ;
7)
;
7)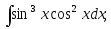 8)
8)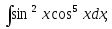
9)
 10)
10) 11)
11)
2.5.2. Метод интегрирования по частям
в неопределенном интеграле
Пусть u = u(x), v = v(x) – дифференцируемые функции. Тогда справедливо равенство (формула интегрирования по частям):
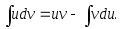
Примеры.

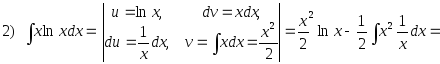
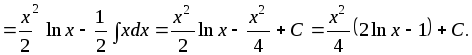

2.56. Найти интегралы, применяя интегрирование по частям:
1)
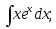 2)
2)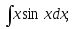 3)
3)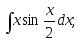 4)
4)
5)
 6)
6) 7)
7)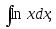 8)
8)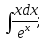
9)
 10)
10)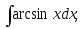 11)
11)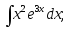 12)
12)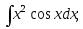
13)
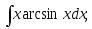 14)
14)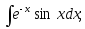 15)
15)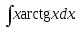
2.57. Найти интегралы:
1)
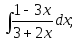 2)
2) 3)
3) ;
4)
;
4)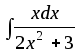 ;
;5)
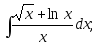 6)
6) ;
7)
;
7) 8)
8)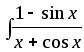 dx;
dx;
9)
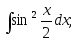 10)
10) ;
11)
;
11)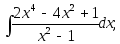 12)
12)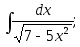
13)
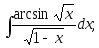 14)
14)
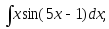 15)
15)
2.6. Определенный интеграл
Определение. Определенным интегралом от функции f(х) называется предел интегральной суммы:

При этом функция f(х) называется подынтегральной функцией, а и b – нижним и верхним пределами интегрирования соответственно.
Укажем свойства определенного интеграла, которые будут необходимы при решении задач:
1.

2.
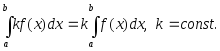
3.
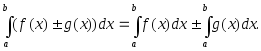
4.
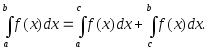
Геометрический смысл определенного интеграла: площадь криволинейной трапеции, ограниченной сверху кривой у = f(х), равна

2.6.1. Правила вычисления определенного интеграла
1. Формула Ньютона–Лейбница:
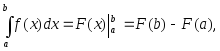
где F′(x) = f(x).
2. Замена переменной:
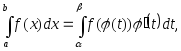
где x =
 – функция, непрерывная вместе с
– функция, непрерывная вместе с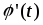 на отрезке
на отрезке
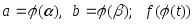 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке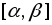 .
.3. Интегрирование по частям:
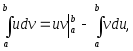
где u = u(x), v = v(x) – дифференцируемые на [a, b] функции.
4. Если f(x) – нечетная функция, то
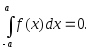
5. Если f(x) – четная функция, то
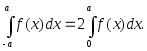
Примеры.
1)
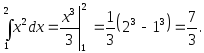
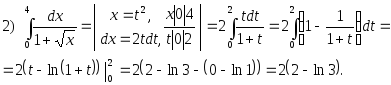
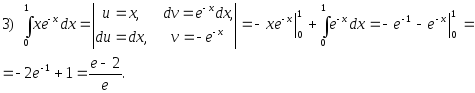
2.58. Вычислить интегралы:
1)
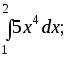 2)
2) 3)
3)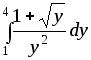 ;
4)
;
4)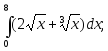
5)
 ;
6)
;
6)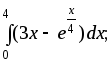 7)
7)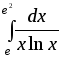 ;
8)
;
8)
9)
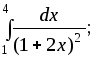 10)
10) 11)
11) ;
12)
;
12)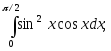
13)
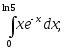 14)
14)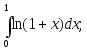 15)
15)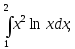 16)
16)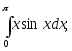
17)
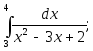 18)
18)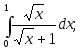 19)
19)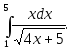
2.6.2. Геометрические приложения
Определенного интеграла
Пример 2.6.
Найти площадь фигуры, ограниченной линиями у = х2, х = у2.
Решение.
Графики функций пересекаются в точках (0; 0), (1; 1) (рис. 2.3).
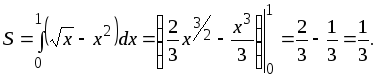

Рис. 2.3. Площадь фигуры
2.59. Найти площадь фигуры, ограниченной графиками функций:
1)
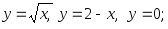 2)
2)
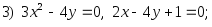
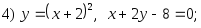
5)
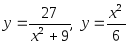 ;
6)
;
6)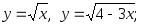
7)
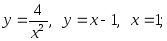 8)
8)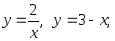
9)
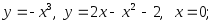 10)
10)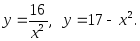
2.60. Найти объем тела, образованного вращением вокруг осей Ох и Оу плоской фигуры, ограниченной линиями:
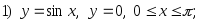 2)
2)
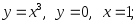
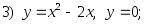 4)
4)
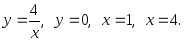
Указание. Объем тела, образованного вращением плоской фигуры вокруг осей координат Ох и Оу, соответственно равен:
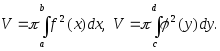
2.61. Найти длину дуги кривой:
1)
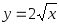 от х = 0 до х = 1; 2)
от х = 0 до х = 1; 2)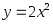 от х = 0 до х = 1;
от х = 0 до х = 1;3)
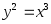 от точки О(0; 0) до точкиА(4;
8).
от точки О(0; 0) до точкиА(4;
8).Указание. Длина дуги кривой
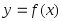 при
при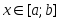 равна
равна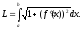
Применение определенного интеграла
В экономике
Дисконтированный доход при непрерывном начислении процентов равен
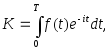
где
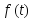 – функция ежегодного дохода;
– функция ежегодного дохода;i – удельная норма процента;
T – время начисления дохода.
2.62. Определить дисконтированный доход за T лет при процентной ставке I %, если первоначальное капиталовложение составило 1 млрд руб. и будет увеличиваться ежегодно на 0,2 млрд руб.:
1) T = 5, i = 10; 2) T = 10, i = 2.
Среднее время, затраченное на изготовление одного изделия в период освоения от
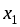 до
до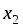 изделий
равно
изделий
равно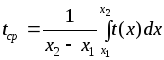 ,
,где функция t = t(x) часто имеет вид
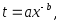
где а – затраты времени на первое изделие;
b – показатель производительности процесса.
2.63. Найти среднее время, затраченное на изготовление одного изделия, если:
1)
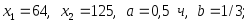
2)
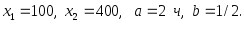
Несобственные интегралы
 .
.Если предел существует и конечен, то интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся.
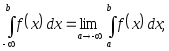

Примеры.
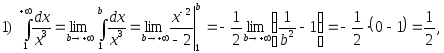
интеграл сходится.
2)
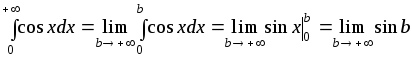 – не существует, интеграл расходится.
– не существует, интеграл расходится.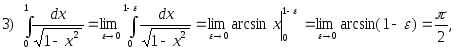
интеграл сходится.
2.64. Вычислить интегралы или установить их расходимость:
1)
 2)
2)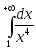 ;
3)
;
3)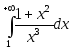 ;
4)
;
4)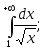 5)
5) ;
;6)
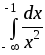 ; 7)
; 7)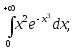 8)
8)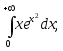 9)
9)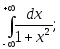 10)
10)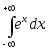
2.65. Вычислить интегралы или установить их расходимость:
1)
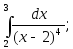 2)
2) 3)
3)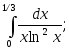
4)
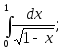 5)
5) 6)
6)
Функции нескольких переменных
