
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9
Определители матриц и их свойства
Для каждой квадратной матрицы существует важная числовая характеристика, называемая определителем матрицы, обозначаемая det A, или |A|, или ∆ – «дельта».
Определение (определителя матрицы).
Если матрица состоит из одного числа: А = (а)1×1, то определитель матрицы равен этому числу det A = a.
Пусть дана квадратная матрица второго порядка из четырех чисел a, b, c, d . Определитель второго порядка вычисляется как разность между произведениями элементов, лежащих на главной и побочной диагоналях:
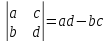 .
.
Например,
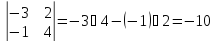 .
.
Определители третьего порядка удобно считать по правилу треугольника. Рассмотрим его схематично (рис. 1.1). Пусть дана квадратная таблица из девяти чисел. Определителем третьего порядка называется число, определяемое равенством:
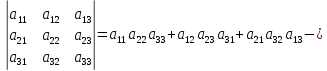
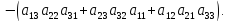
Для практики вычислений удобно пользоваться схемой: первые три слагаемые в правой части равенства представляют собой произведения трех элементов определителя, взятых, как показано пунктирами на (рис. 1.1) слева. Чтобы получить следующие три члена, нужно перемножить элементы определителя по три так, как показано пунктирами на той же схеме справа, и взять их с противоположным знаком (рис. 1.1).
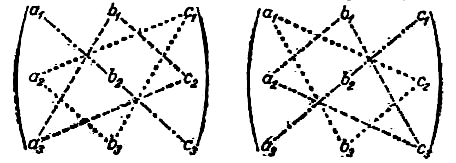
Рис. 1.1. Правило треугольника для вычисления определителя
Пример 1.3. Вычисление определителя по правилу треугольника.

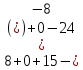 .
.
Определители высших порядков можно вычислить, раскладывая их по любой выбранной строке или столбцу, сведением к определителям меньших размерностей по формуле:
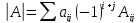 .
Суммирование ведется по одному индексу.Аij
называется алгебраическим дополнением
к элементу аij
, это определитель матрицы меньшего
порядка, получаемый из матрицы А
вычеркиванием i-строки и j-го
столбца.
.
Суммирование ведется по одному индексу.Аij
называется алгебраическим дополнением
к элементу аij
, это определитель матрицы меньшего
порядка, получаемый из матрицы А
вычеркиванием i-строки и j-го
столбца.
Пример 1.4. Вычисление определителя четвертого порядка разложением по первой строке.
 = 1 ٠
= 1 ٠
 –2 ٠
–2 ٠ + 2 ٠
+ 2 ٠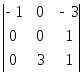 –0٠
–0٠
 =
= 1 ٠(3–18)
– 2٠(2+1)
+ 2٠(–3)=
–15 – 6 – 6 = –27.
=
= 1 ٠(3–18)
– 2٠(2+1)
+ 2٠(–3)=
–15 – 6 – 6 = –27.
1.4. Вычислить определители 2-го и 3-го порядков:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)![]() ;
4)
;
4)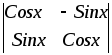 ;
;
5)
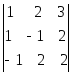 ;
6)
;
6)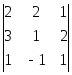 ;
7)
;
7)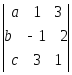 ;
8)
;
8)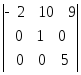 .
.
1.5. Вычислить определители матриц (табл. 1.3) разложением по элементам целесообразно выбранной строки (столбца).
Таблица 1.3
|
№ |
1 |
2 |
3 |
4 |
|
Матрица |
1 0 3 1 0 1 –1 2 2 –1 1 0 –1 0 1 4 |
2 3 –1 1 1 0 –1 2 0 –3 0 1 1 2 3 0 |
1 2 2 0 –1 0 1 –3 0 0 –2 1 0 3 1 1 |
4 6 –2 4 1 2 –3 1 4 –2 1 0 6 4 4 6 |
Обратная матрица. Решение матричных уравнений
Определение. Матрица А–1 называется обратной к матрице А, если А٠А–1 = А–1٠А = Е.
Теорема. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.
Обратная матрица находится по формуле:
 ,
где Т – транспонирование матрицы, а
,
где Т – транспонирование матрицы, а
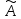 – присоединенная матица, состоящая из
алгебраических дополнений.Аij
– это определитель матрицы меньшего
порядка, получаемый из матрицы А
вычеркиванием i-строки и j-го
столбца, взятый со знаком
– присоединенная матица, состоящая из
алгебраических дополнений.Аij
– это определитель матрицы меньшего
порядка, получаемый из матрицы А
вычеркиванием i-строки и j-го
столбца, взятый со знаком
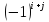 .
.
Для
матриц размера
 обратная матрица может быть найдена по
формуле:
обратная матрица может быть найдена по
формуле:
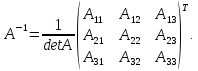
1.6. Найти обратные матрицы для следующих матриц (табл. 1.4)
Таблица 1.4
|
№ |
1 |
2 |
3 |
4 |
5 |
|
Матрица |
1 2 3 4 |
3 4 5 7 |
–3 2 4 2 1 0 1 0 1 |
2 5 7 6 3 4 5 –2 –2 |
1 2 3 0 1 2 0 0 1 |
1.7.
При каких значениях
![]() матрица А не имеет обратной:
матрица А не имеет обратной:
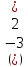 ;
2)
;
2)
 ;
; 3)
3)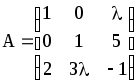 .
.
Пример 1.5. Решение матричного уравнения.
Пусть
дано матричное уравнение
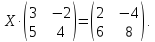
Нужно найти матрицу Х.
Обозначим
А =![]() ,
а В =
,
а В =![]() ,
тогда имеем уравнение Х ٠
А
= В. Умножим обе части справа
на А–1:
,
тогда имеем уравнение Х ٠
А
= В. Умножим обе части справа
на А–1:
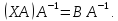 Применяя
ассоциативность умножения матриц,
Применяя
ассоциативность умножения матриц,
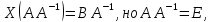
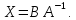
При решении матричных уравнений важно следить за тем, с какой стороны нужно умножать, в силу неперестановочности умножения матриц.
Найдем матрицу А–1 , предварительно вычислим определитель:
![]()
![]()
![]()
![]()
![]()
Найдем
А![]() =
=![]()
 =
=![]()
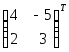 =
=![]() .
.
Итак,
![]()
Проверка:
![]() – верно.
– верно.
1.8. Решить матричное уравнение:
1)
![]() ;
2)
;
2)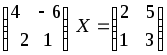 ;
;
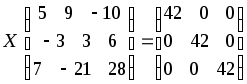 ;
4)
;
4)
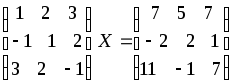 ;
;
5)
![]() ;
6)
;
6)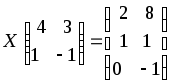 .
.
