
- •Математика
- •Глава 1 подготовлена м. Н. Рассказовой, глава 2 – о. П. Диденко, предисловие, введение, глава 3, алфавитно-предметный указатель – с. Х. Мухаметдиновой.
- •Оглавление
- •Предисловие
- •Введение
- •Глава 1. Элементы линейной алгебры и аналитической геометрии
- •Линейная алгебра
- •Операции над матрицами
- •Свойства операций над матрицами:
- •Определители матриц и их свойства
- •Обратная матрица. Решение матричных уравнений
- •Системы линейных уравнений
- •Построение моделей задач, сводящихся к системам линейных уравнений
- •1.1.6. Применение элементов линейной алгебры в экономике
- •1.1.7. Модель Леонтьева межотраслевого баланса
- •Контрольные задания
- •Векторная алгебра
- •Векторы. Линейные операции над векторами
- •Скалярное, векторное, смешанное произведение векторов
- •Линейные операторы. Собственные векторы и собственные значения
- •Контрольные задания
- •Аналитическая геометрия
- •Прямая на плоскости
- •Окружность. Эллипс. Гипербола. Парабола
- •Прямая и плоскость в пространстве
- •Контрольные задания
- •Глава 2. Математический анализ
- •2.1. Функции одной переменной
- •Контрольные задания
- •2.2. Предел и непрерывность функции
- •Некоторые свойства пределов
- •2.2.1. Замечательные пределы
- •2.2.2. Непрерывность функции в точке
- •Контрольные задания
- •2.3.2. Применение производной в экономике
- •2.3.3. Дифференциал функции
- •Контрольные задания
- •2.4. Приложения производной
- •2.4.1. Исследование функции на монотонность,
- •Экстремумы и выпуклость.
- •Асимптоты графика функции
- •2.4.2. Общая схема исследования функции
- •И построения ее графика
- •Контрольные задания
- •2.5.2. Метод интегрирования по частям
- •2.6.2. Геометрические приложения
- •Определенного интеграла
- •Применение определенного интеграла
- •В экономике
- •Несобственные интегралы
- •Функции нескольких переменных
- •2.7.1. Частные производные, дифференциал,
- •Градиент функции
- •2.7.2. Частные производные 2-го порядка.
- •Исследование функции на экстремум
- •2.7.3. Метод наименьших квадратов
- •Контрольные задания
- •2.8. Дифференциальные уравнения
- •1. Уравнение с разделяющимися переменными
- •2. Однородные уравнения 1-го порядка
- •3. Линейные уравнения 1-го порядка
- •4. Линейные однородные уравнения 2-го порядка
- •С постоянными коэффициентами
- •2.9. Последовательности и ряды
- •2.9.1. Предел последовательности
- •2.9.2. Числовые ряды
- •Достаточный признак расходимости ряда
- •Признаки сходимости рядов с положительными членами:
- •2.9.3. Степенные ряды
- •Контрольные задания
- •3.1.3. Размещения
- •Сочетания
- •Если в формуле (3.5) заменить число k на n − k, то получим:
- •Правило сложения
- •Правило произведения
- •Контрольные вопросы
- •Элементы теории вероятностей
- •3.2.1. Основные понятия теории вероятностей
- •3.2.2. Классификация событий
- •3.2.3. Алгебра событий
- •3.2.4. Статистический подход к понятию вероятности
- •3.2.5. Классический подход к понятию вероятности
- •3.2.6. Решение вероятностных задач
- •С помощью комбинаторики
- •3.2.7. Геометрический подход к понятию вероятности
- •3.2.8. Аксиоматическое определение
- •Понятия вероятности
- •3.2.9. Вероятность суммы несовместных событий
- •3.2.10. Вероятность произведения событий
- •3.2.11. Формула полной вероятности. Формула Байеса
- •3.2.12. Формула Бернулли. Наивероятнейшее число
- •Наступлений события
- •3.2.13. Локальная формула Муавра−Лапласа
- •3.2.14. Интегральная формула Муавра−Лапласа
- •3.2.15. Формула Пуассона
- •Контрольные вопросы
- •3.3. Случайные величины
- •3.3.1. Дискретные случайные величины.
- •Закон распределения дискретной случайной величины
- •3.3.2. Числовые характеристики
- •Дискретных случайных величин
- •Свойства математического ожидания:
- •Свойства дисперсии:
- •3.3.3. Функция распределения вероятностей
- •Случайной величины
- •Основные свойства функции распределения:
- •3.3.4. Непрерывная случайная величина.
- •3.3.5. Числовые характеристики
- •Непрерывных случайных величин
- •3.3.6. Равномерное распределение
- •3.3.7. Нормальное распределение
- •3.3.8. Показательное распределение
- •Контрольные вопросы
- •3.4. Элементы математической статистики
- •Основные задачи математической статистики
- •3.4.1. Основные понятия математической статистики
- •3.4.2. Точечные оценки параметров распределения
- •3.4.3. Интервальные оценки параметров распределения
- •Интервальные оценки параметров нормального распределения:
- •3.4.4. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении
- •Генеральной совокупности по критерию Пирсона
- •Алгоритм применения критерия Пирсона
- •Контрольные вопросы
- •Заключение
- •Библиографический список
- •Основная литература
- •Дополнительная литература
- •Приложение 1
- •Приложение 2
- •Приложение 3
- •Приложение 4
- •Приложение 5
- •Приложение 6
- •Глава 2 «Математический анализ»
- •Глава 3 «Теория вероятностей и математическая статистика»
- •3.1. Классическое определение вероятности
- •Теоремы сложения и умножения вероятностей
- •Формулы полной вероятности и Байеса
- •3.4. Схема Бернулли. Теорема Муавра-Лапласа, Пуассона
- •3.5. Случайные величины
- •3.6. Законы распределения
- •3.7. Математическая статистика
- •Алфавитно-предметный указатель
- •Математика
- •644099, Омск, ул. Красногвардейская, 9

2. Постоянный множитель можно выносить за знак математического ожидания:
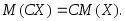
3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей:
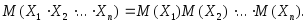
4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых:
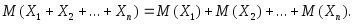
Характеристиками рассеяния значений дискретной случайной величины вокруг математического ожидания служат дисперсия и среднее квадратическое отклонение.
Определение. Дисперсией
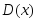 дискретной
случайной величины называется
математическое ожидание квадрата
отклонения случайной величины от её
математического ожидания:
дискретной
случайной величины называется
математическое ожидание квадрата
отклонения случайной величины от её
математического ожидания: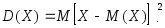 (3.25)
(3.25)Дисперсию удобно вычислять по формуле:
 (3.26)
(3.26)где
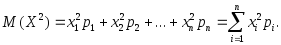 (3.27)
(3.27)Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю:
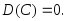
2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат:
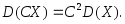
3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых:

Определение. Средним квадратическим отклонением случайной величины называется квадратный корень из дисперсии:
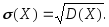 (3.28)
(3.28)Пример 3.43. Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины
 ,
закон распределения которой представлен
в видетаблицы
3.9.
,
закон распределения которой представлен
в видетаблицы
3.9.Таблица 3.9
Закон распределения дискретной случайной величины
−5
2
3
4
0,4
0,3
0,1
0,2
Математическое ожидание найдем по формуле (3.24):
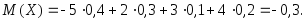
Дисперсию вычислим по формуле (3.26), для этого найдем
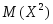 по формуле (3.27):
по формуле (3.27):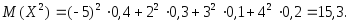
Далее найдем дисперсию:
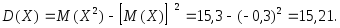
Вычислим среднее квадратическое отклонение по формуле (3.28):
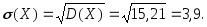
Пример 3.44. Найти математическое ожидание случайной величины
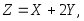 если математические ожидания случайных
величин
если математические ожидания случайных
величин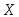 и
и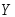 соответственно равны
соответственно равны и
и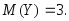
Используя свойства математического ожидания 2 (постоянный множитель можно выносить за знак математического ожидания) и 4 (математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых) получим:
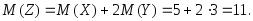
Пример 3.45. Случайные величины
 и
и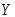 независимы. Найти дисперсию случайной
величины
независимы. Найти дисперсию случайной
величины если
если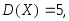
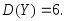
Так как случайные величины
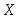 и
и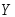 независимы, то также независимы
случайные величины
независимы, то также независимы
случайные величины и
и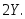
Используя свойства дисперсии 2 (постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат) и 3 (дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим:
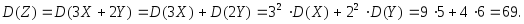
3.3.3. Функция распределения вероятностей
Случайной величины
Определение. Функцией распределения называют функцию
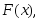 определяющую для каждого значения
определяющую для каждого значения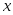 вероятность того, что случайная величина
вероятность того, что случайная величина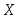 примет значение, меньшее
примет значение, меньшее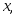 т. е.
т. е.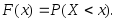
Замечание. Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».
Основные свойства функции распределения:
1. Функция распределения принадлежит отрезку
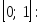
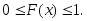
2. Функция распределения является неубывающей функцией:
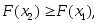 если
если

Следствие. Вероятность того, что случайная величина
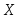 примет значение, заключенное в интервале
примет значение, заключенное в интервале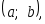 равна приращению функции распределения
на этом интервале:
равна приращению функции распределения
на этом интервале:
3. Если все возможные значения случайной величины
 принадлежат интервалу
принадлежат интервалу то:
то: при
при

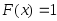 при
при
Следствие. Справедливы следующие предельные соотношения:
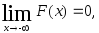
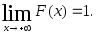
Пример 3.46. Закон распределения дискретной случайной величины
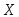 представлен в видетаблицы
3.10.
представлен в видетаблицы
3.10.Таблица 3.10
Закон распределения дискретной случайной величины
2
4
7
0,5
0,2
0,3
Найти функцию распределения
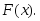
Если
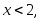 то
то так как значений меньше числа 2 случайная
величина
так как значений меньше числа 2 случайная
величина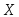 принимать не может.
принимать не может.Если же
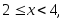 то
то Это обусловлено тем, что значение 2
случайная величина
Это обусловлено тем, что значение 2
случайная величина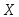 принимает с вероятностью 0,5.
принимает с вероятностью 0,5.При
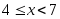 функция распределения
функция распределения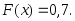 Действительно, случайная величина
Действительно, случайная величина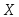 принимает значение 2 с вероятностью
0,5 и значение 4 с вероятностью 0,2.
Следовательно, одно из этих значений
случайная величина может принять
(теорема о вероятности суммы несовместных
событий) с вероятностью:
принимает значение 2 с вероятностью
0,5 и значение 4 с вероятностью 0,2.
Следовательно, одно из этих значений
случайная величина может принять
(теорема о вероятности суммы несовместных
событий) с вероятностью:0,2 + 0,5 = 0,7.
В случае, когда
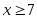 функция распределения
функция распределения поскольку событие, связанное с тем,
что случайная величина принимает
значения
поскольку событие, связанное с тем,
что случайная величина принимает
значения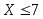 является достоверным и его вероятность
равна единице.
является достоверным и его вероятность
равна единице.Итак, искомая функция распределения имеет вид:
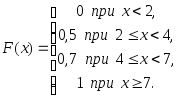
3.3.4. Непрерывная случайная величина.
Плотность распределения.
Вероятность попадания случайной величины
в заданный интервал
Определение. Непрерывной случайной величиной Х, заданной на некотором интервале
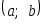 или
или
 ,
называется
такая случайная величина, которая
может принимать в результате серии
испытаний любое значение из интервала
,
называется
такая случайная величина, которая
может принимать в результате серии
испытаний любое значение из интервала
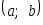 или
или
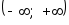 .
.Определение. Плотностью распределения вероятностей непрерывной случайной величины
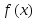 называется предел отношения вероятности
попадания значения непрерывной
случайной величины в интервал
называется предел отношения вероятности
попадания значения непрерывной
случайной величины в интервал
 к
к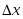 при
при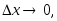 если такой предел существует:
если такой предел существует:
Свойства плотности распределения:
1. Плотность распределения неотрицательна, т. е.
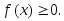
2. Несобственный интеграл от плотности распределения в пределах от
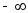 до
до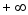 равен
единице:
равен
единице: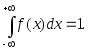
В частности, если все возможные значения непрерывной случайной величины
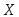 находятся в интервале
находятся в интервале ,
то
,
то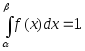
Определение. Функция распределения вероятностей
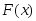 непрерывной случайной величины
непрерывной случайной величины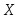 равна несобственному интегралу от
плотности распределения
равна несобственному интегралу от
плотности распределения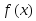 с переменным верхним пределом:
с переменным верхним пределом: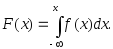 (3.29)
(3.29)Исходя из выше изложенного, плотность вероятности можно определить как первую производную от функции распределения:
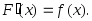 (3.30)
(3.30)Теорема. Пусть
 − плотность распределения вероятностей
непрерывной случайной величины
− плотность распределения вероятностей
непрерывной случайной величины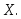 Тогда
вероятность
попадания значения случайной величины
Тогда
вероятность
попадания значения случайной величины
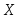 в интервал
в интервал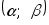 равна определенному интегралу от
функции
равна определенному интегралу от
функции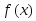 в пределах от
в пределах от до
до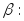
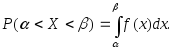 (3.31)
(3.31)Пример 3.47. Дана функция распределения непрерывной случайной величины Х:
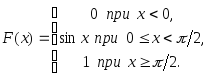
Найти плотность распределения

Плотность распределения равна первой производной от функции распределения:
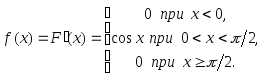
Заметим, что при
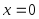 производная
производная не существует.
не существует.Пример 3.48. Дана плотность распределения непрерывной случайной величины

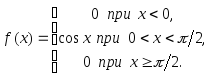
Найти функцию распределения
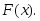
Используем формулу

Если
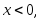 то
то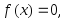 следовательно,
следовательно,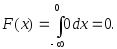
Если
 то
то
Если
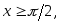 то
то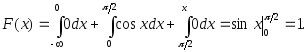
Таким образом, функция распределения
 имеет вид:
имеет вид: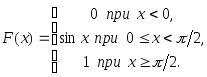
Пример 3.49. Дана плотность распределения непрерывной случайной величины Х:
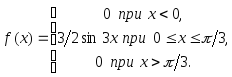
Найти вероятность того, что непрерывная случайная величина
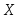 примет значение из интервала
примет значение из интервала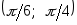 .
.Воспользуемся формулой (3.30):
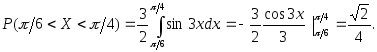
3.3.5. Числовые характеристики
Непрерывных случайных величин
Математическое ожидание
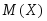 непрерывной
случайной величины Х,
возможные значения которой принадлежат
всей оси 0х,
определяется
равенством:
непрерывной
случайной величины Х,
возможные значения которой принадлежат
всей оси 0х,
определяется
равенством: 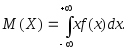 (3.32)
(3.32)Дисперсия
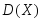 непрерывной
случайной величины Х,
возможные значения которой принадлежат
всей оси 0х,
определяется
равенством:
непрерывной
случайной величины Х,
возможные значения которой принадлежат
всей оси 0х,
определяется
равенством: 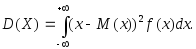 (3.33)
(3.33)Среднее квадратическое отклонение непрерывной случайной величины, как и для дискретной случайной величины, определяется равенством:
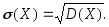 (3.34)
(3.34)Пример 3.50. Дана плотность распределения непрерывной случайной величины Х:
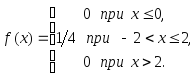
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.
Найдем математическое ожидание по формуле (3.31):
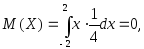
т. к. подынтегральная функция начетная, а пределы интегрирования симметричны относительно начала координат.
Дисперсию найдем по формуле (3.32):
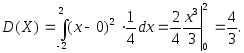
И, наконец, среднее квадратическое отклонение равно:

3.3.6. Равномерное распределение
Определение. Равномерным называют распределение вероятностей непрерывной случайной величины
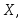 если на интервале
если на интервале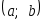 ,
которому принадлежат все возможные
значения
,
которому принадлежат все возможные
значения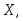 плотность сохраняет постоянное значение
и задается следующим образом:
плотность сохраняет постоянное значение
и задается следующим образом:Математическое ожидание, дисперсия и среднее квадратическое отклонение случайной величины, распределенной равномерно, соответственно равны:
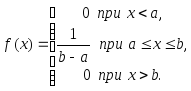
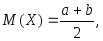
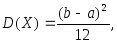

Пример 3.51. Цена деления шкалы амперметра 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при округлении ошибка будет превышать 0,02 А.
Ошибку округления показаний прибора можно рассматривать как случайную величину
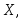 распределенную равномерно в интервале
между целыми делениями.
распределенную равномерно в интервале
между целыми делениями.Поскольку интервал
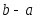 равен цене деления амперметра, т. е.
0,1. При этом ошибка округления будет
удовлетворять условию, если будет
принадлежать интервалу
равен цене деления амперметра, т. е.
0,1. При этом ошибка округления будет
удовлетворять условию, если будет
принадлежать интервалу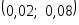 .
Тогда плотность распределения имеет
вид:
.
Тогда плотность распределения имеет
вид:
По формуле (3.30) найдем соответствующую вероятность:
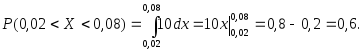
3.3.7. Нормальное распределение
Определение. Нормальным называют распределение вероятностей непрерывной случайной величины Х, плотность которого имеет вид:
где
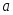 − математическое ожидание;
− математическое ожидание;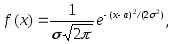
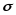 −среднее
квадратическое отклонение.
−среднее
квадратическое отклонение. Вероятность попадания значения случайной величины
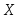 в интервал
в интервал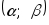 равна:
равна: ,
(3.35)
,
(3.35)где
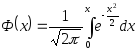 − функция Лапласа, значения которой
представлены вприложении
2.
− функция Лапласа, значения которой
представлены вприложении
2.Вероятность того, что абсолютная величина отклонения меньше положительного числа
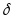 равна:
равна: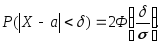 (3.36)
(3.36)В частности, при
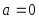 справедливо равенство:
справедливо равенство: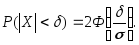 (3.37)
(3.37)Пример 3.52. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины
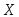 соответственно равны 10 и 2. Найти
вероятность того, что случайная величина
соответственно равны 10 и 2. Найти
вероятность того, что случайная величина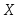 примет значение, заключенное в интервале
примет значение, заключенное в интервале .
.Воспользуемся формулой (3.30), учитывая, что
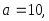
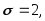
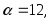
 получим:
получим:
Значения
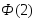 и
и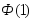 найдены из таблицыприложения
2.
найдены из таблицыприложения
2.Пример 3.53. Случайные ошибки измерения
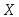 подчинены нормальному закону
распределения со средним квадратическим
отклонением
подчинены нормальному закону
распределения со средним квадратическим
отклонением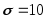 мм.
Найти вероятность того, что измерение
будет произведено с ошибкой, не
превосходящей по абсолютной величине
мм.
Найти вероятность того, что измерение
будет произведено с ошибкой, не
превосходящей по абсолютной величине
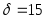 мм.
мм.Математическое ожидание случайных ошибок равно нулю, поэтому, используя формулу (3.36), получим:
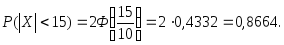
3.3.8. Показательное распределение
Определение. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины
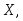 плотность которого имеет вид:
плотность которого имеет вид:где
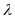 − постоянная положительная величина.
− постоянная положительная величина.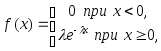
Функция распределения показательного закона:
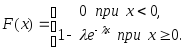
Вероятность попадания в интервал
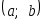 непрерывной случайной величиныХ,
распределенной по показательному
закону, вычисляют по формуле:
непрерывной случайной величиныХ,
распределенной по показательному
закону, вычисляют по формуле: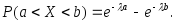 (3.38)
(3.38)Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного закона распределения соответственно равны:

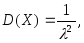
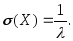 (3.39)
(3.39)Пример 3.54. Непрерывная случайная величина распределена по показательному закону с плотностью, равной:

Найти вероятность того, что в результате испытаний значение непрерывной случайной величины
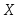 попадет в интервал
попадет в интервал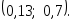
По формуле (3.37) найдем:
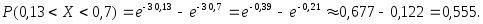
Контрольные вопросы
1. Сформулировать определение понятия дискретной случайной величины.
2. Что представляет собой закон распределения дискретной случайной величины?
3. Как вычисляются математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины?
4. Сформулировать определение понятия непрерывной случайной величины.
5. Сформулировать определение понятий плотности распределения вероятности и функции распределения непрерывной случайной величины.
6. Как вычисляются математическое ожидание, дисперсия и среднее квадратическое отклонение непрерывной случайной величины?
7. Как вычисляется вероятность попадания непрерывной случайной величины в заданный интервал?
3.4. Элементы математической статистики
В результате экономических, социологических, политологических и других исследований получают большие массивы статистических данных. Например, изучают распределение студентов первого курса г. Омска по росту (весу, состоянию здоровья, успеваемости и т. д.). Практически любой признак поддается непосредственному измерению либо может получить условную числовую характеристику. При этом некоторый признак элементов совокупности можно рассматривать как случайную величину, принимающую те или иные числовые значения с определенной вероятностью. В реальных исследованиях вероятность случайной величины оценивается с помощью ее относительной частоты при достаточно большом числе испытаний.
Основные задачи математической статистики
1. Определение методов сбора и группировки статистических сведений, полученных в результате экспериментов или наблюдений.
2. Разработка методов анализа статистических данных: оценка неизвестной вероятности, оценка зависимости случайной величины от других случайных величин и др.
3.4.1. Основные понятия математической статистики
Определение. Генеральной совокупностью называется совокупность всех элементов, обладающих интересующими исследователей признаками.
Определение. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных элементов из генеральной совокупности.
Определение. Объемом совокупности называется количество элементов, содержащихся в этой совокупности. Например, если из 2000 изделий отобрано для обследования случайным образом 100 изделий, то объем генеральной совокупности N = 2000, а объем выборки n = 100.
Определение. Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности. Пусть из генеральной совокупности извлечена выборка объема n, в которой значение x1 некоторого исследуемого признака X (размер одежды, заработная плата и пр.) наблюдалось n1 раз, значение x2 − n2 раз, … , значение xk − nk раз.
Определение. Значения xi (i = 1, 2, 3, …, k) исследуемого признака X называются вариантами, а их последовательность, записанная в возрастающем порядке, − вариационным рядом.
Определение. Число ni, показывающее сколько раз наблюдалось значение xi некоторого признака X в исследуемой совокупности, называется частотой.
Определение. Отношение частоты значения xi некоторого признака X в исследуемой совокупности к объему выборки n называется относительной частотой:
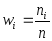 .
(3.40)
.
(3.40)Необходимо отметить, что всегда выполняются равенства:
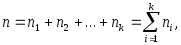 (3.41)
(3.41)
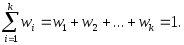 (3.42)
(3.42)Определение. Размах выборки (обозначается
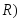 − разность
между максимальным и минимальным
значениями случайной величины,
полученными при исследовании выборки
или длина интервала, которому принадлежат
все значения варианты выборки:
− разность
между максимальным и минимальным
значениями случайной величины,
полученными при исследовании выборки
или длина интервала, которому принадлежат
все значения варианты выборки: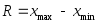 .
.Определение. Мода (обозначается
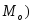 – наиболее часто встречающееся значение
случайной величины (исследуемого
признака), полученное при исследовании
выборки.
– наиболее часто встречающееся значение
случайной величины (исследуемого
признака), полученное при исследовании
выборки.Определение. Ломаная, отрезки которой соединяют точки с координатами (хi; ni), где хi – числовые значения исследуемого признака, а ni – частота их появления в выборке, называется полигоном частот.
Наряду с полигоном частот можно построить полигон относительных частот, для этого по оси ординат необходимо откладывать относительные частоты
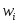 .
.Определение. Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению
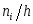 (плотность частоты).
(плотность частоты).Площадь частичного i-го прямоугольника равна сумме частот, попавших в i-й интервал. Площадь гистограммы частот равна сумме всех частот, т. е. объему выборки n.
Определение. Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению
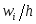 (плотность относительной частоты).
(плотность относительной частоты).Площадь частичного i-го прямоугольника равна относительной частоте вариант, попавших в i-й интервал. Площадь гистограммы относительных частот равна единице.
Пример 3.55. Пусть исследуемый признак X – размер обуви мальчиков 9-х классов одной из школ имеет следующее распределение по частотам, представленное в виде таблицы 3.11.
Таблица 3.11
Распределение случайной величины по частотам
хi – размер обуви
38
39
40
41
42
43
44
45
ni − частота (количество учеников, имеющих определенный размер обуви)
2
2
5
7
6
4
3
1
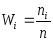 −относительная
частота
−относительная
частота
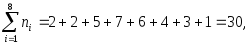
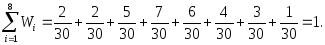
Размах и мода соответственно равны:
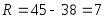 и
и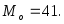
3.4.2. Точечные оценки параметров распределения
Определение. Статистической оценкой
 неизвестного параметра
неизвестного параметра
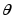 теоретического распределения называют
функцию
теоретического распределения называют
функцию от наблюдаемых случайных величин
от наблюдаемых случайных величин
Определение. Точечной называют статистическую оценку, которая определяется одним числом
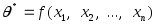 ,
где
,
где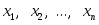 − результаты
− результаты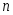 наблюдений над количественным признаком
наблюдений над количественным признаком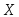 (выборка).
(выборка).Определение. Несмещенной называют точечную оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки.
Определение. Смещенной называют точечную оценку, математическое ожидание которой не равно оцениваемому параметру при любом объеме выборки.
Несмещенной оценкой математического ожидания (генеральной средней) служит выборочная средняя:
 (3.43)
(3.43)где
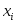 − варианта выборки;
− варианта выборки;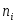 −частота
варианты
−частота
варианты
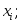
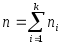 −объем
выборки.
−объем
выборки.Смещенной оценкой генеральной дисперсии служит выборочная дисперсия:
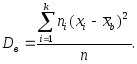 (3.44)
(3.44)Более удобна для вычислений формула:
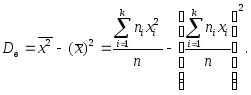
Несмещенной оценкой генеральной дисперсии служит исправленная выборочная дисперсия:
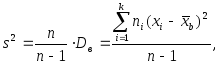 (3.45)
(3.45)Пример 3.56. В итоге пяти измерений длины стержня одним прибором (без систематических ошибок) получены следующие результаты (в мм): 92; 94; 103; 105; 106. Найти: а) выборочную среднюю длину стержня; б) выборочную и исправленную дисперсии ошибок прибора.
а) найдем выборочную среднюю по формуле (3.38):
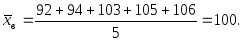
б) найдем выборочную дисперсию по формуле (3.39):
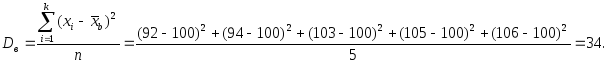
Найдем исправленную дисперсию по формуле (3.40):

3.4.3. Интервальные оценки параметров распределения
Определение. Интервальной называют оценку, которая определяется двумя числами − концами интервала, покрывающего оцениваемый параметр.
Определение. Доверительным называют интервал, который с заданной надежностью
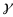 покрывает заданный интервал.
покрывает заданный интервал.Интервальные оценки параметров нормального распределения:
1. Интервальной оценкой (с надежностью
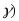 математического
ожидания
математического
ожидания
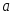 нормально
распределенного количественного
признака
нормально
распределенного количественного
признака
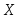 по выборочной средней
по выборочной средней
 служит доверительный интервал:
служит доверительный интервал: а) при известном среднем квадратическом отклонении
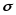 генеральной совокупности
генеральной совокупности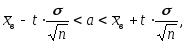 (3.46)
(3.46)где
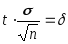 −
точность оценки;
−
точность оценки;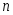 −объем
выборки;
−объем
выборки;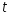 −значение
аргумента функции Лапласа
−значение
аргумента функции Лапласа
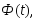 при котором
при котором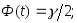
б) при неизвестном среднем квадратическом отклонении
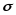 генеральной совокупности
генеральной совокупности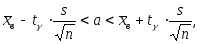 (3.47)
(3.47)где
 −
«исправленное» выборочное среднее
квадратическое отклонение;
−
«исправленное» выборочное среднее
квадратическое отклонение;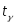 −находятся
по таблице приложения
2
по заданным
−находятся
по таблице приложения
2
по заданным
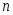 и
и
2. Интервальной оценкой (с надежностью
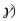 среднего
квадратического отклонения
среднего
квадратического отклонения
 нормально распределенного количественного
признака
нормально распределенного количественного
признака по «исправленному» выборочному среднему
квадратическому отклонению
по «исправленному» выборочному среднему
квадратическому отклонению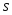 служит доверительный интервал:
служит доверительный интервал: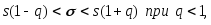 (3.48)
(3.48)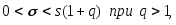
где
 находятся по таблицеприложения
4
по заданным
находятся по таблицеприложения
4
по заданным
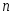 и
и
Пример 3.57. Найти доверительный интервал для оценки математического ожидания
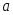 нормально
распределенного количественного
признака
нормально
распределенного количественного
признака
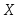 надежностью 0,95, если генеральное
среднее квадратическое отклонение
надежностью 0,95, если генеральное
среднее квадратическое отклонение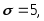 выборочное среднее
выборочное среднее а объем выборки
а объем выборки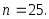
Доверительный интервал найдем по формуле (3.43). Все величины известны, кроме
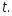 Значение
Значение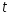 найдем из соотношения
найдем из соотношения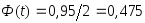 и
затем находим
и
затем находим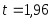 по
таблицеприложения
4.
Подставив все известные значения в
формулу, получим искомый доверительный
интервал 12,04
по
таблицеприложения
4.
Подставив все известные значения в
формулу, получим искомый доверительный
интервал 12,04
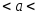 15,96.
15,96.Пример 3.58. По данным выборки объема
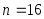 из генеральной совокупности найдено
«исправленное» выборочное среднее
квадратическое отклонениеS=1
нормально
распределенного количественного
признака X.
Найти доверительный интервал, покрывающий
генеральное среднее квадратическое
отклонение
из генеральной совокупности найдено
«исправленное» выборочное среднее
квадратическое отклонениеS=1
нормально
распределенного количественного
признака X.
Найти доверительный интервал, покрывающий
генеральное среднее квадратическое
отклонение
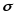 с надежностью 0,95.
с надежностью 0,95.По данным задачи
 и
и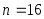 в таблицеприложения
4
найдем
в таблицеприложения
4
найдем
 Поскольку
Поскольку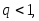 то используя формулу (3.43) найдем искомый
интервал
то используя формулу (3.43) найдем искомый
интервал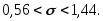
3.4.4. Проверка статистических гипотез
Определение. Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
Определение. Нулевой (основной) называют выдвинутую гипотезу

Определение. Статистическим критерием называют случайную величину
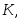 которая служит для проверки гипотезы.
которая служит для проверки гипотезы.Определение. Наблюдаемым (эмпирическим) значение
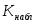 называют то значение критерия, которое
вычислено по выборкам.
называют то значение критерия, которое
вычислено по выборкам.Определение. Областью принятия гипотезы (область допустимых значений) называют совокупность значений критерия, при которых принимают нулевую гипотезу.
Определение. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.
Основной принцип проверки гипотез: если наблюдаемое значение критерия принадлежит критической области, то нулевую гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то нулевую гипотезу принимают.
Проверка гипотезы о нормальном распределении
Генеральной совокупности по критерию Пирсона
Пусть эмпирическое распределение задано в виде последовательности равноотстоящих вариант и соответствующих им частот (табл. 3.12):
Таблица 3.12
Закон распределения дискретной случайной величины
…
…
Алгоритм применения критерия Пирсона
1. Выдвигают нулевую гипотезу о нормальном законе распределения случайной величины X и находят его параметры
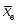 и
и
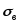 по
формулам (3.38) и (3.33) соответственно.
по
формулам (3.38) и (3.33) соответственно.2. Определяют теоретические частоты
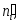 соответствующие опытным частотам
соответствующие опытным частотам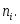 Если
среди опытных частот имеются
малочисленные, то их необходимо
объединить с соседними. Интервалы
после объединения будем обозначать
(
Если
среди опытных частот имеются
малочисленные, то их необходимо
объединить с соседними. Интервалы
после объединения будем обозначать
(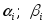 ].
Число интервалов должно быть не менее
4-х. Если случайная величинаX
непрерывна, то
].
Число интервалов должно быть не менее
4-х. Если случайная величинаX
непрерывна, то 
где
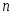 − объем выборки (сумма всех частот);
− объем выборки (сумма всех частот);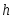 −шаг
(разность между двумя соседними
вариантами);
−шаг
(разность между двумя соседними
вариантами); 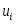 вычисляют
следующим образом:
вычисляют
следующим образом: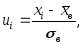
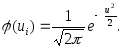 (3.49)
(3.49)Значения
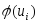 находят
из таблицыприложения
1.
находят
из таблицыприложения
1.3. Вычисляют наблюдаемое значение критерия:
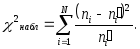 (3.50)
(3.50)4. Находят по таблице критических точек распределения
 по заданному уровню значимости
по заданному уровню значимости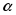 и числу степеней свободы
и числу степеней свободы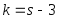
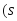
 −
− число
групп выборки)
находят критическую точку
число
групп выборки)
находят критическую точку
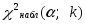 правосторонней
критической области.
правосторонней
критической области.5. Если
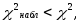 то гипотезу о нормальном распределении
выборки принимают; если
то гипотезу о нормальном распределении
выборки принимают; если
 то гипотезу о нормальном распределении
выборки отвергают.
то гипотезу о нормальном распределении
выборки отвергают.Пример 3.59. Используя критерий Пирсона при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности
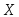 с эмпирическим распределением выборки
(табл.
3.13)
объема
с эмпирическим распределением выборки
(табл.
3.13)
объема

Таблица 3.13
Закон распределения дискретной случайной величины
5
7
9
11
13
15
17
19
21
15
26
25
30
26
21
24
20
13
Используя формулы (3.38) и (3.33), найдем выборочную среднюю
 и выборочное среднее квадратическое
отклонение
и выборочное среднее квадратическое
отклонение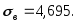
Вычислим теоретические частоты, учитывая, что
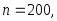
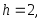
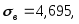 по формуле (3.41):
по формуле (3.41):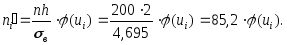
Составим расчетную таблицу 3.14.
Таблица 3.14
Расчетная таблица
1
5
−1,62
0,1074
9,1
15
34,81
3,8
2
7
−1,20
0,1942
16,5
26
90,25
5,5
3
9
−0,77
0,2966
25,3
25
0,09
0,0
4
11
−0,35
0,3752
32
30
4,00
0,1
5
13
0,08
0,3977
33,9
26
62,41
1,8
6
15
0,51
0,3503
29,8
21
77,44
2,6
7
17
0,93
0,2589
22
24
4,00
0,2
8
19
1,36
0,1582
13,5
20
42,25
3,1
9
21
1,78
0,0818
7
13
36,00
5,1
∑
200
По таблице критических точек распределения
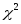 (приложение
5)
по уровню значимости
(приложение
5)
по уровню значимости
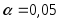 и числу степеней свободы
и числу степеней свободы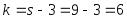 находим критическую точку правосторонней
критической области:
находим критическую точку правосторонней
критической области: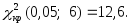
Поскольку
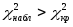 − гипотезу о нормальном распределении
генеральной совокупности отвергаем,
т. е. эмпирические и теоретические
частоты различаются
значимо.
− гипотезу о нормальном распределении
генеральной совокупности отвергаем,
т. е. эмпирические и теоретические
частоты различаются
значимо.Контрольные вопросы
Каковы основные задачи математической статистики?
Сформулировать определение понятия генеральной совокупности.
Сформулировать определение понятия выборочной совокупности.
Что называется объемом совокупности?
Какая выборка называется репрезентативной?
Что называется вариационным рядом?
Что называется частотой, относительной частотой варианты?
Что называется размахом выборки?
Что называется модой выборки?
Что называется размахом, модой выборки?
Что представляет собой диаграмма частот, относительных частот?
Сформулировать определение понятия статистической гипотезы.
Сформулировать определение понятия статистического критерия.
Какие оценки параметров распределения называются точечными?
Как вычислить несмещенную оценку математического ожидания?
Как вычислить смещенную оценку математического ожидания?
Как вычислить несмещенную оценку дисперсии?
Как вычислить смещенную оценку дисперсии?
Какие оценки параметров распределения называются интервальными?
Какое распределение называется нормальным?
