Замечание. То, что случайная величина примет одно из значений последовательности
…,
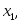
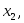является достоверным событием,
следовательно, выполняются условия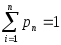
и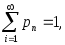
если
значения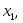
…,
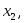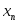являются членами конечной или бесконечной
последовательности соответственно.Пример 3.41. Вероятность попадания в цель первым стрелком 0,8; вторым – 0,7; третьим – 0,9. Каждый стрелок выстрелил по мишени. Составить закон распределения дискретной случайной величины
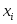− числа попаданий в мишень. Какова
вероятность того, что хотя бы один
стрелок попадет в цель?Пусть событие
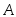– попадание в цель первым стрелком,
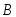– вторым,
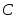– третьим. Вероятности противоположных
им событий соответственно равны: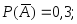
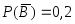и
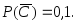
Случайная величина
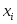может принимать следующие значения:
0, 1, 2 и 3. Вычислим значения вероятностей,
соответствующие этим значениям
дискретной случайной величины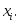
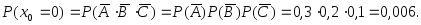
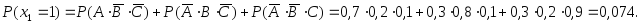
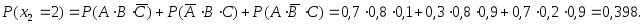
Запишем полученные результаты в виде таблицы 3.6 − закона распределения дискретной случайной величины.
Таблица 3.6
Закон распределения дискретной случайной величины
0
1
2
3
0,074
Проверка.
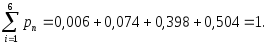
Пример 3.42. Монету подбрасывают 8 раз. Составить закон распределения дискретной случайной величины − числа выпадений орла.
Поскольку в условии задачи говорится о серии независимых испытаний, в каждом из которых событие, связанное с выпадением орла может произойти с вероятностью
и не произойти с вероятностью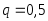
,
то мы имеем дело со схемой Бернулли.
Следовательно, функциональная
зависимость вероятности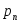
от значений случайной величины
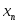может быть выражена формулой Бернулли
,
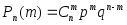где
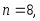а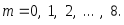
Вычислим вероятности, соответствующие значениям дискретной случайной величины
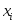от 0 до 8: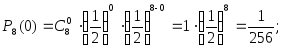
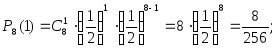
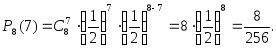
Полученные результаты запишем в виде таблицы 3.7, т. е. представим таблично закон распределения дискретной случайной величины.
Таблица 3.7
Закон распределения дискретной случайной величины
0
1
2
3
4
5
6
7
8
На основе табличных данных (табл. 3.6) построим многоугольник распределения вероятностей (рис. 3.1), т. е. представим графически закон распределения дискретной случайной величины.
Рис. 3.1. Многоугольник распределения вероятностей
Рассмотренный в задаче закон распределения дискретной случайной величины, выраженной формулой Бернулли, получил название биноминального закона распределения.
3.3.2. Числовые характеристики
Дискретных случайных величин
Дискретная случайная величина
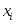задана законом распределения,
представленным втаблице
3.8.
Таблица 3.8
Закон распределения дискретной случайной величины
…
…
Определение. Математическим ожиданием
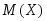дискретной
случайной величины называется сумма
произведений всех возможных значений
случайной величины и соответствующих
им значений вероятности: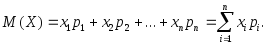
(3.23)Если дискретная случайная величина принимает бесконечное счетное множество значений, то математическое ожидание представляет собой ряд:
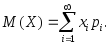(3.24)В этом случае математическое ожидание существует, если ряд, представленный в правой части равенства (3.24), сходится абсолютно.
Свойства математического ожидания:
Математическое ожидание постоянной величины равно самой постоянной: