2. 3. 7. Обернена функція

Нехай функція задана на множині і - її множина значень. Візьмемо і знайдемо (таке хоча б одне, обов’язково знайдеться, бо - з множини значень функції), причому таких може бути не одне. Якщо то видно , що на множині задана деяка нова функція з множиною значень , яку логічно назвати оберненою до функції Те, що було для даної функції областю визначення для нової стало множиною значень і навпаки. Позначатимемо обернену функцію

Якщо функція має обернену на множині то функцію називають оборотною на цій множині. В протилежному випадку її називають необоротною. Безпосередньо з означення оборотності функції одержується наступна

Теорема 1. Для того, щоб функція була оборотною на множині необхідно і достатньо, щоб

Доведення цієї теореми пропонуємо провести самостійно.

Із цієї теореми зразу випливає

Наслідок. Якщо - строго монотонна на то вона тут і оборотна.

Чи вірне обернене твердження? Можна придумати не монотонну і оборотну на множині функцію, (і тим більше не монотонну і необоротну!). Очевидно, що графіки функцій та будуть співпадати, бо це одне і теж рівняння тільки написане по-різному. Якщо ми в останній рівності замінимо на а на (це ми робимо виключно для зручності, тому що звикли аргумент позначати а значення функції ), то після таких позначень обернена функція запишеться у вигляді Графік оберненої функції функції записаної вже в такому вигляді вже буде відрізнятися від графіка функції Якщо графіку прямої функції належатиме точка то графіку оберненої функції належить точка яка буде симетричною попередній точці відносно прямої Отже, графіки функцій і симетричні відносно прямої

З’ясуємо далі питання про те, як, маючи певні властивості функції, які гарантуватимуть її оборотність, одержати властивості оберненої функції.

Теорема 2 (Про існування та неперервність оберненої функції). Якщо функція монотонно-зростаюча (спадна) і неперервна на відрізку , то на відрізку існує обернена функція яка монотонно-зростаюча (спадна) і неперервна на цьому відрізку.

Доведення. 1)Існування випливає із монотонності на відрізку і попереднього наслідку.

2) Візьмемо для конкретності монотонно-зростаюча на Для доведення монотонності оберненої функції візьмемо Очевидно, що або, що те саме і Припустимо, що Тоді із монотонного зростання функції на відрізку отримаємо, що а це суперечить тому, що Отже, з того що а це означає, що монотонно-зростаюча на відрізку

3)Неперервність випливає з того, що:

а) - монотонно зростаюча на

б)множиною значень є відрізок

і залишається тільки використати доведену раніше теорему. Теорема доведена.

Зауваження. Ця теорема залишається вірною і у випадку, коли замість відрізка брати інтервал причому і не обов’язково мусять бути скінченними числами.

Нехай функція монотонно зростаюча (спадна), неперервна на і Тоді на інтервалі існує обернена функція яка тут монотонно зростаюча (спадна) і неперервна (ми не виключаємо випадку, що чи або обидва будуть відповідними нескінченностями). Покажемо деякі застосування тільки-що доведених теорем.

І) Доведемо спочатку існування кореня довільного степеня з довільного додатнього дійсного числа. Для цього розглянемо функцію на

1. Ясно, що ця функція тут неперервна.

2. Візьмемо

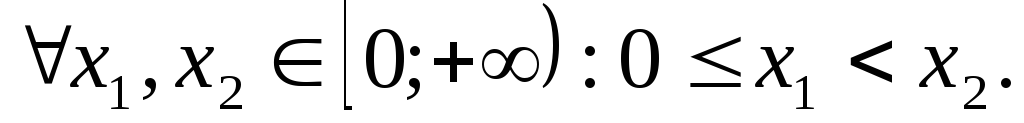
Далі, тому

отже функція на - монотонно-зростаюча.

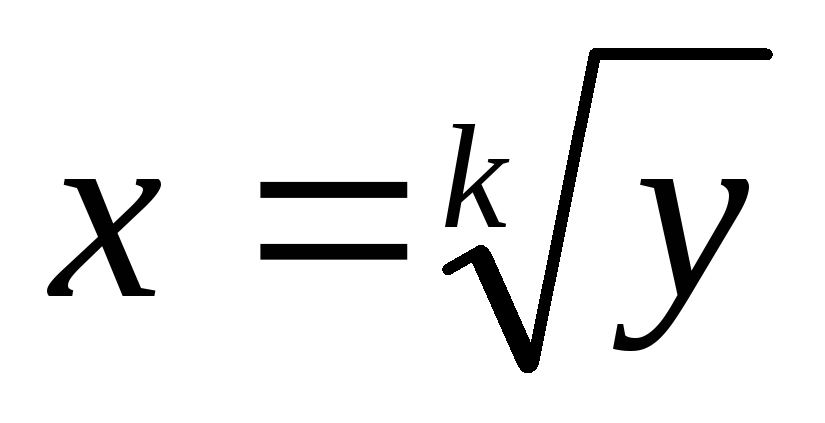3. Значить за попередніми теоремами на множині значень існуватиме функція обернена до функції а це означає, що яке б ми з 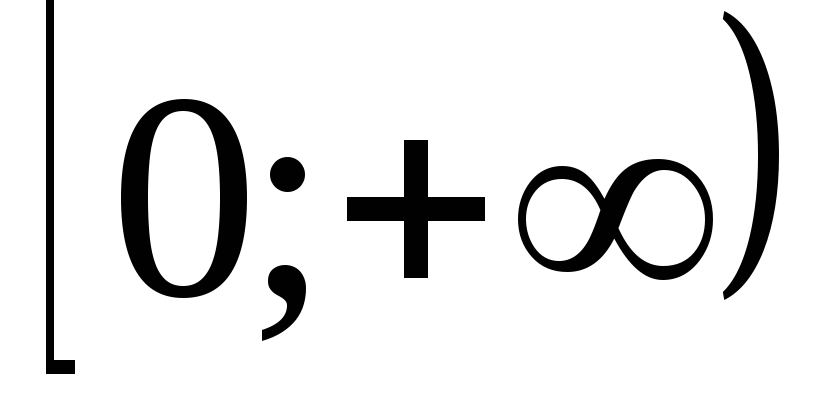не взяли, завжди існуватиме

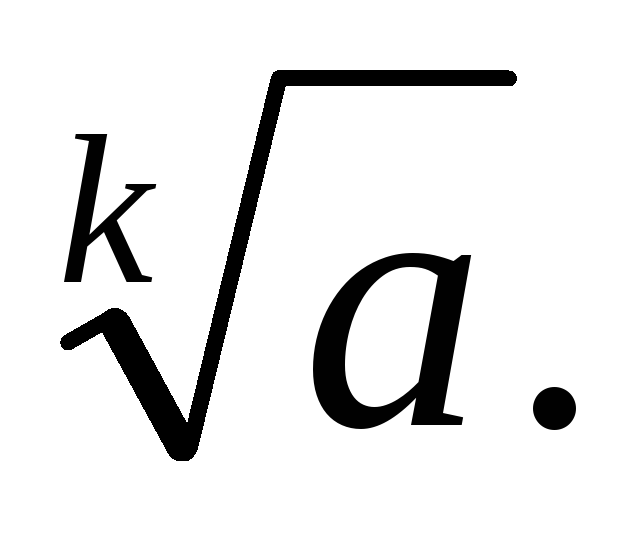
Очевидно, що отримана тільки-що функція на піввідрізку теж буде неперервною і монотонно зростаючою. Після перепозначення змінних отримаємо: Її графік симетричний графіку відносно прямої

Зауваження. Функція при -непарному буде оборотною на всій числовій осі.

ІІ )Існування обернених тригонометричних функцій .

Розглянемо функцію Очевидно вона на всій області визначення оборотною не буде, бо можна підібрати Проте, якщо розглянемо на відрізку то тут функція - неперервна, монотонно-зростаюча з множиною значень Значить, за теоремою про існування оберненої функції, на відрізку існує обернена функція до функції яка також є неперервною, монотонно зростаючою на з множиною значень Очевидно, що ми функцію на предмет оборотності можемо розглядати і на інших відрізках Але ці обернені функції, які ми одержимо в цих випадках будуть відрізнятися від тільки-що введеної хоча б множиною значень.

Зауважимо, що кожну з таких обернених функцій можна одержати з основної шляхом додавання до неї деяких констант і множенням її на (-1).

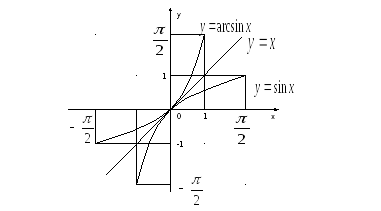
О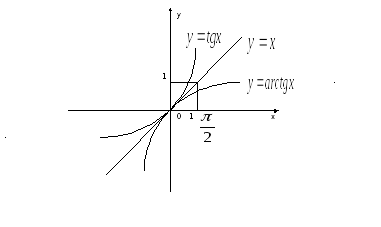держана вище обернена функція до функції взята на найзручнішому проміжку (за принципом близькості його до початку координат). Аналогічно одержуємо (розглянувши на ), (розглянувши на ), (розглянувши на ).

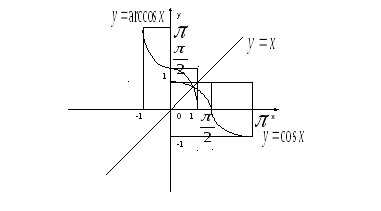
Наступним етапом застосування тільки-що вивченої теорії є одержання функції оберненої до показникової. Але спочатку треба вивчити саму показникові функцію. Їй присвячений наступний розділ.