4. 4. 5. Площа поверхні обертання

Нехай функція неперервна разом зі своєю першою похідною на . Нехай графік цієї функції обертається навколо осі . В результаті опишеться поверхня, знайдемо її площу.

Оскільки ми вміємо шукати площу поверхні, яку опише, обертаючись навколо осі, деякий відрізок, то візьмемо довільне розбиття відрізка . Утворимо на нашій кривій точки , . З’єднаємо ці точки послідовно ламаною лінією (причому будемо вважати, що серед точок цього розбиття обов’язково присутні ті, в яких цей графік перетинає вісь ).

Знайдемо спочатку площу поверхні, яку опише та ланка ламаної. Очевидно, це буде бічна поверхня або циліндра, або конуса, або зрізаного конуса. Ми знаємо, що бічна поверхня всіх цих трьох об’єктів обчислюється за формулою . Знайдемо величину твірної цієї поверхні .

Тоді бічна поверхня, яку опише наш відрізок, буде шукатися за формулою:

Отже, площа поверхні, яку опише ламана буде дорівнювати:

Зрозуміло, що ця величина буде наближеним значенням шуканої площі поверхні. Причому точність тим вища чим менший крок розбиття. Тому дамо Означення 1. Під площею поверхні, яка утворюється від обертання вказаної вище кривої навколо , будемо розуміти

якщо ця границя існує.

Ясно, що не є інтегральною сумою, проте, оскільки , значить знаходиться як завгодно близько і до точки і до точки , а оскільки функція є неперервною, то близьке до , а значить сума близька до такої

.

А ця сума є інтегральною для функції , яка, як ми знаємо, за умовою є неперервною, а отже інтегрованою на . Тому

Отже, ми встановили, що вказана вище поверхня має площу і вона обчислюється за формулою

Так само як і при обчисленні довжини дуги можна стверджувати, що якщо крива задана параметрично.

Отже, нехай – функція, неперервна на відрізку разом зі своїми першим похідними.

Означення 2. Площа поверхні, яка утвориться внаслідок обертання цієї кривої навколо шукається

.

Зауважимо, що використовуючи отримані формули легко одержувати площі поверхні кулі і її частин.

4. 4. 6. Координати центра ваги матеріальної дуги та пластинки. Теореми Гульдена

Отже, нехай – функція, неперервна на відрізку разом зі своїми першим похідними. Нехай крива, яка задається системою цих функцій є матеріальною, однорідною кривою з лінійною густиною (). Поставимо перед собою завдання знайти координати центра ваги цієї кривої. Для цього будемо користуватися наступним відомим з механіки фактом. Якщо ми маємо скінченну систему точок , і масою , та координати центра ваги такої системи шукаються з функції:

; .

Поступимо наступним чином.

Візьмемо розбиття відрізка .

Цьому розбиттю на кривій відповідатиме система точок з координатами . Ці точки розіб’ють нашу криву на елементарні матеріальні дуги. Знайдемо довжину, а потім масу кожної з цих елементарних дуг.

Шукаємо довжину.

Тоді маса цієї дуги буде дорівнювати

Зосередимо далі масу цієї елементарної дуги в точці , яка лежить на тій тій дузі. Проробивши все це зі всіма елементарними дугами ми замінимо нашу матеріальну криву системою із матеріальних точок, координати і маси кожної з яких відомі. Тоді за вище заданим відомим із механіки фактом, координати центра ваги цієї системи будуть шукатися за формулами.

;

.

Міркуючи далі так само, як ми це робили при інших заданнях інтеграла Рімана, логічно за координати центра ваги нашої матеріальної прямої розуміти:

;

(Якщо вони існують).

Але чисельники виразів і є інтегральними сумами для і , обидві з яких на за умовою нашої задачі є неперервними, а отже інтегрованими, а отже вказані вище границі існують, то ми отримаємо наступні формули для обчислення.

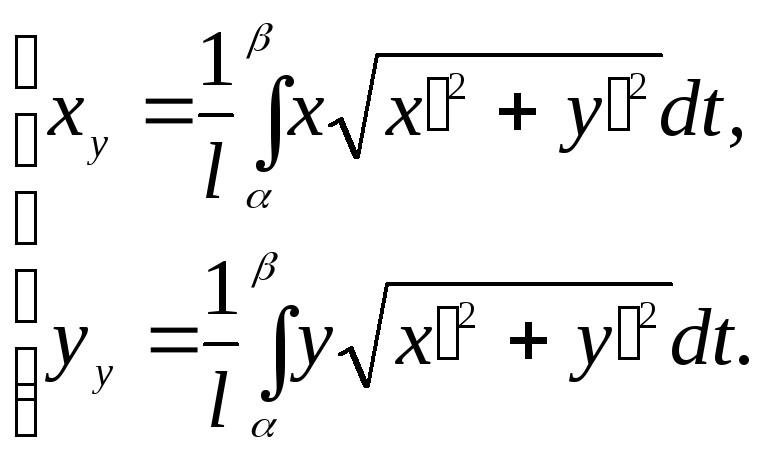
Зрозуміло, що з допомогою отриманих формули одержимо аналогічні формули для або в полярних координатах. Проаналізуємо дещо вище формулу для ординати центра ваги і перепишемо цю формулу в такому вигляді:

Остання рівність може бути записана у вигляді такого твердження

Теорема 1 (І Гульдена).

Площа поверхні, яка утвориться від обертання кривої навколо осі, яка не перетинає цієї кривої дорівнює добутку довжини цієї кривої на довжину кола, радіус якого дорівнює відстані до цієї осі від центра ваги цієї кривої.

Розв’яжемо аналогічну задачу для однорідної матеріальної пластинки.

Нехай і неперервні на функції, причому Розглянемо трапецію, яка обмежена прямими і і графіками обох цих функцій. Будемо вважати цю трапецію пластинкою з плоскою густиною ().

Знову поставимо задачу знайти центр ваги цього об’єкта. Візьмемо розбиття відрізка :

Через точки проведемо прямі, паралельні до осі , які розіб’ють нашу пластинку на штук матеріальних пластинок. Попрацюємо з тою пластинкою. Візьмемо . Тоді замінимо цю елементарну трапецію прямокутником, ширина якого буде лежати на відрізку , а довжина дорівнюватиме . Знайдемо масу цього прямокутника:

.

Зосередимо масу того прямокутника в центрі ваги цього прямокутника (точка перетину діагоналей). Ця точка матиме координати

.

Проробивши таке саме з іншими трапеціями знову замінимо нашу криво лінійну трапецію системою таких матеріальних точок.

Тоді

;

.

Для того, щоб визначити центр ваги нашої матеріальної пластики достатньо знайти і Нескладний аналіз показує, що ці границі існуватимуть і ми отримаємо наступні формули для обчислення координат матеріальної пластинки, яка задається явно в декартових координатах.

Розглянемо частковий випадок, отриманий результат, коли на . Тоді друга формула матиме вигляд Останню рівність можна переписати у вигляді

Остання рівність може бути записана у вигляді теореми

Теорема 2 (ІІ Гульдена).

Об’єм тіла, яке утвориться від обертання криволінійної трапеції навколо осі, яку вона не перетинає дорівнює добутку площі цієї трапеції на довжину кола, яке описує центр ваги цієї трапеції.

РОЗДІЛ V. ОЛІМПІАДНІ ЗАДАЧІ

Нескладно встановити, що

Виникає питання, що буде, коли чисел буде . Для відповіді на це запитання розв’яжемо такі задачі:

1. Нехай – додатні числа такі, що

Довести, що

Доведення.

Бажаючи довести цю задачу методом математичної індукції зробимо наступні дії.

1. Перевіримо правильність нерівності при .

, ,. – виконується

, ,,

(Останнє легко перевірити )

2. Припустимо, що наше твердження вірне при .

, ,

3. Доведемо, що таке твердження вірне при .

, ,

(Якщо всі числа , то випадок придоведений).

Припустимо, що не всі числа рівні 1. Значить серед них є принаймі одне, яке менше за 1, а отже і обов’язково має бути хоча б одне, яке більше за 1.

Не зменшуючи загальності можна вважати, що

, . (*)

Розглянемо такі числа:

такі, що

Звідси за припущенням (при ) будемо мати, що

.

Перетворимо цю рівність

Для доведення такого твердження достатньо показати, що

А, враховуючи (*) маємо, що

Отже, наше твердження вірне при і задача розв’язана.

Зауважимо, що рівність в нерівності буде виконуватися лише тоді, коли .

Використовуючи цю задачу, ми доведемо нерівність Коші між середнім геометричним і середнім арифметичним будь-якої скінченої кількості чисел.

2. .

Нехай .

Ця нерівність справедлива якщо хоча б одне з чисел дорівнює 0. Тому припустимо, що наші числа не дорівнюють 0.

Візьмемо

Тоді

Значить звідси, за задачею 1, будемо мати, що

Нерівність доведена.

Використовуючи тільки що доведену нерівність Коші,з’ясуємо ще одне співвідношення між деякими середніми.

2. Нехай маємо . Запишемо нерівність Коші для чисел

Перетворимо

Отже, ми встановили, що середнє геометричне більше за середнє гармонійне.

Середнє арифметичне середнє геометричнесереднє гармонійне.

Для того, щоб зв’язати з цими середніми ще й середнє квадратичне треба довести ще одну допоміжну рівність:

4.

Перепишемо цю нерівність в такому рівносильному вигляді

Припустимо, що в нас є 2 числа

.

Виходячи звідси можна встановити, що ліва частина може бути зображена у вигляді

Таким чином наша нерівність доведена, причому ми встановили, що рівність в даній нерівності буде у випадку, коли всі числа рівні між собою.Поділимо обидві частини в нерівності на.

З цієї нерівності зразу ж одержуємо

Якщо ж поставити умову, що всі числа додатні, то одержимо таку нерівність

Величина називається середнім квадратичним чисел . Отже одержуємо, що

середнє квадратичнесереднє арифметичнесереднє геометричнесереднє гармонійне

Розглянемо деякі приклади, які приводять нас до деяких відомих нерівностей.

Приклад 1.

Нехай – довільні додатні числа. Довести, що

(1)

Розв’язок.

Розглянемо неперервну функцію

при .

Продиференціювавши одержуємо

.

Звідси робимо висновок, що

при

при

при

Таким чином функція в точцінабуває свого найменшого значення на множині, і , як наслідок

, (2)

причому знак рівності досягається лише при . Підставившив (1) одержуємо

Звідки і випливає рівність (1).

Відмітимо, що рівність в (1) буде тільки в тому випадку, коли .

Зауваження.Із нерівності (1) в якості наслідку можна одержати деякі класичні нерівності: про середнє арифметичне і середнє геометричне, нерівність Гельдера, Коші-Буняковського та інші.

Справді, переписавши нерівність (1) в вигляді

і замінивши в ньому на, ана, одержимо

.

Звідси, використовуючи метод математичної індукції, легко довести, що, які б не були додатні числа імає місце нерівність

(3)

в якій рівність досягається тільки в тому випадку, коли

.

Тепер, підставивши в (3) і() одержуємо

(4)

якщо в (4) , то одержуємо нерівність між середнім арифметичним і середнім геометричним чисел:

(5)

Вибираючи в (4) числа так, щоб виконувалася рівність, одержуємо нерівність

(6)

У всіх трьох нерівностях (4)-(6) рівність досягається тільки в тому випадку, коли . З нерівності (6) випливає нерівність

, (7)

де і.

Справді, з (6) випливає, що

.

Підставивши ііі() в (7) одержуємо нерівність Гельдера

(8)

Із (8) при одержимо нерівність Коші-Буняковського

. (9)

При цьому рівність (8) і (9) буде лише тоді, коли

Приклад 2. Довести, що при.

Розвязок.

Нехай – будь-яке додатнє число. Розглянемо функціюна проміжку. За теоремою Лагранжа маємо

тобто

,

де . Так, якпри будь-якому, то звідси одержуємо

,

тобто для будь-якого додатного числа.

Зауваження. Із нерівності

,

яка справедлива при будь-якому значенні , в якості простого наслідку можна одержати, наприклад, класичну нерівність між середнім арифметичним і середнім геометричним додатніх чисел(а також і інші класичні нерівності). Нехай– додатні числа і. Так як за доведеним

...........................

то, перемноживши ці нерівності, одержимо нерівність

,

тобто нерівність

,

або

.

Покажемо, як з допомогою тільки що доведених різних класичних нерівностей можна розв’язувати деякі серйозні олімпіадні задачі.

Задача 1.

Довести, що для чисел з відрізкавиконується нерівність

Розв’язання.

Скористаємося нерівністю Коші-Буняковського стосовно векторів

Тоді

Оскільки нерівність симетрична, то, не обмежуючи загальності, можна вважати, що Тодізвідки

Але звідки отримуємо

Тоді

Звідси та з попередньої оцінки отримуємо твердження задачі.

Задача 2.

Дано дійсні числа , всі вони більші за одиницю і такі, щодовести нерівність

Розв’язання.

За допомогою нерівності Коші для трьох чисел послідовно оцінимо ліву частину нерівності:

Задача 3.

Довести, що коли добуток довільних додатних чисел дорівнює 1, то виконується нерівність

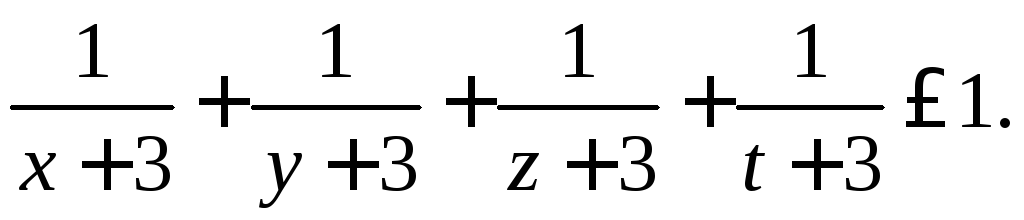
Розв’язання.

Дана нерівність при умовах задачі рівносильна такій:

або, після перетворень,

яка справедлива внаслідок виконання умови та нерівностей

ВИСНОВКИ

Результати роботи:

1. Досліджене поняття електронного підручника, визначені його основні переваги та недоліки;

2. Розроблений повний теоретичний курс з теорії границь, Диференціального та Інтегрального числення функції однієї змінної;

3. Підібрані технології для ефективного та зручного використання при створенні електронного посібника;

4. Розроблений «Електронний підручник з математичного аналізу».

На основі виконаної роботи зроблені висновки:

1. Використання електронного посібника сприяє підвищенню ефективності засвоєння знань, умінь та навичок;

2. Перевагою над «паперовим» аналогом є можливість редагування, змін в дизайні, перевидання.

3. Використані програмні засоби (HTML, Advanced Grapher) можуть вивчатися вчителями як засіб організації навчального процесу.

4. Робота з електронним підручником формує в учнів навички самостійної роботи з матеріалом, вміння знаходити необхідну інформацію, працювати з графічними об’єктами.

5. Можливі напрями застосування даного електронного підручника:

• В навчальному процесі математичних шкіл та ліцеїв;

• В навчальному процесі на молодших курсах університетів.

ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ

1. Шевченко В.Л. Зміст підготовки педагогічних кадрів щодо проектування комп’ютерно орієнтованих дидактичних засобів та використання комп’ютерних педагогічних технологій у навчальному процесі. // Вісник післядипломної освіти: Збірник наукових праць Центрального інституту післядипломної педагогічної освіти АПН України - Вип.3. - К., 2006.- С. 210-222.

2. Рамський Ю.С., Іваськів І.С., Ніколаєнко О.Ю. Вивчення Web-програмування в школі: Навчальний посібник. – Тернопіль: Навчальна книга – Богдан, 2004. – с.45-98.

3. Агеев В.Н. Электронные учебники и автоматизированные обучающие системы. Лекция- доклад / РАН; Институт проблем информатики; Российская академия естественных наук. Институт фундаментальной и прикладной информатики / Н.А. Селезнева (общ.ред.). — М.: Исследовательский центр проблем качества подготовки специалистов, 2001. – 80 c.

4. Антонова С. Г., Тюрина Л. Г. Современная учебная книга. Создание учебной литературы нового поколения: Учеб. пособие для студ. вузов, обуч. по направлению "Книжное дело" и спец. "Издательское дело и редактирование". - М. : Агенство "Издательский сервис", 2001. – 288c.

5. Беспалько А.А. Технологические подходы к разработке электронного учебника по информатике: Дисс.канд. пед. наук. - Екатеринбург, 1998. – 132 c.

6. Беспалько В.П. Слагаемые педагогической технологии. - М.:  Педагогика, 1989. – 190 c.

7. Давидов М.О. Курс математичного аналізу, ч.2, Київ: Вища школа, 1991.

8. Демидович Б.П. Сборник задач и упражнений по математическому анализу, М.: Наука, 1990.

9. Иванов В.Л. Структура електронного учебника. //Інформатика и образование. – 2001. - №6.

10. Ильин В.А., Садовничий В.А., Сендов Бл.Х. Математический анализ, МГУ, 1979.

11. Кудрявцев А.Д. Краткий курс математического анализа, М.: Наука, 1989.

12. Кудрявцев Л.Д. Курс математического анализа, М.:Высшая школа, 1981.

13. Кузнецов М.Л. Сборник задач по высшей математике, М.,1983.

14. Ляшко С.И, Боярчук А.К, Александрович И.Н. Сборник задач и упражнений по математическому анализу, ч 1, М., 2001.

15. Рамський Ю.С., Іваськів І.С., Ніколаєнко О.Ю. Вивчення Web-програмування в школі: Навчальний посібник. – Тернопіль: Навчальна книга – Богдан, 2004.

16. Рудин У. Основы математического анализа, М.:Мир, 1976.

17. Христочевский С.А. Электронные мультимедийные учебники и энциклопедии.// Информатика и образование. 2000 - №2.

Додаток 1.

Об’єднанням двох множин і() називається множина, кожний елемент якої є або елементом множиниабо елементом множини

Перерізом множин і() називається множина, яка складається з тих і тільки тих елементів, які одночасно є елементами і множиниі множини

Різницею множин і() назвемо множину, яка складається з тих елементів множиниякі не є елементами множини

Симетричною різницею двох множин і() називається множинаОчевидно, щоТепер домовимось про позначення основних числових множин, якими ми будемо далі користуватися.

Послідовністю називається функція, областю визначення якої є множина всіх натуральних чисел.

Монотонно зростаючою (спадною) називається послідовність , якщо будь-який член цієї послідовності, починаючи з другого більший (менший) за попередній, або коротко_.

Монотонно неспадною (незростаючою) називається послідовність , якщо:

().

Монотонною називається послідовність , якщо вона є або монотонно зростаючою (спадною), або монотонно незростаючою (неспадною).

Нижньою (верхньою) межею послідовності називається число, якщо

Обмеженою знизу (зверху) називається послідовність , якщо вона має нижню (верхню) межу.

Обмеженою називається послідовність , якщо вона обмежена і знизу і зверху абоякщо ж хоча б одного з чиселчине існує, то послідовністьназиваєтьсянеобмеженою.

Модулем числа називається числояке визначається так

- околом точки (позначається це -) називається проміжок з центром в точці, довжиноюі кінці якого до нього не включаються або що те саме

Нескінченно малою називається послідовність , якщо

Границею послідовності називається число і записуєтьсяякщо послідовність- нескінченно мала.

Збіжною називається послідовність, яка має границю, в протилежному випадку вона є – розбіжною.

Нескінченно великою називається послідовність , якщо

Граничною точкою множини називається точка якщо в будь-якому околі цієї точки є безліч елементів множини

Границею функції в точці(або при) називається числоі записуєтьсяякщо для будь-якої послідовностітакої що,матимемо, що послідовністьзбігається до числа _{(означення за Гейне)}

Границею функції в точціназивається числоякщо _{(означення Коші)}

Границею функції в точціназивається число якщо _{(означення Коші 2)}

Правосторонньою границею функції в точці називається число і записується або якщо в будь-якому правому півоколі точки є безліч елементів з множини

Правосторонньою границею функції в точці називається число і записується або (або що те саме ).

(означення за Коші)

Правосторонньою границею функції в точці називається число і записується або якщо

1)

2)

3)

послідовність - збіжна до числа (означення за Гейне).

Лівосторонньою границею функції в точці називається число і записується або якщо

1)

2)

3)

послідовність - збіжна до числа (означення за Гейне)

Лівосторонньою границею функції в точці називається число і записується або якщо

(або що те саме ). (означення за Коші)

Неперервною в точці називається функція_, якщо і

Точкою усувного розриву називається точка з області визначення функції, якщо в цій точціпроте.

Точкою розриву І роду називається точка з області визначення функції називається, якщо в цій точці не існує границя функції, проте існують скінченні односторонні границі (без сумніву не рівні між собою).

Точкою розриву ІІ роду називається точка з області визначення функції, якщо в цій точці також не існує границя функції, проте при цьому не існує хоча б одна з її односторонніх границь.

Оборотною на деякій множині називається функція , якщо вона має обернену на цій множині.

Кутовим коефіцієнтом прямої називаєтьсякута нахилу цієї прямої до осі.

Похідною функції в точці називається границя , коли , (якщо вона існує) і позначається

Похідна функції в точці – це границя відношення приросту функції в цій точці до приросту аргументу, коли приріст аргументу прямує до нуля.

Дотичною до кривої в точці називається граничне положення січної_, коли _{– довільна точка на даній кривій}, відмінна від _.

Диференційованою в точці з інтервалуназивається функція_, якщо приріст цієї функції можна зобразити у вигляді

,

де – число, незалежне від, а– нескінченно мала функція при, тобто

Похідною ІІ порядку функції називається похідна від похідної цієї функції.

Диференціалом ІІ порядку функції будемо називати диференціал від диференціала цієї функції.

Диференціалом n-го порядку n разів диференційована в точці функції називається диференціал від диференціала (n-1)-го порядку цієї функції в цій точці.

Точкою мінімуму функції називається точка , якщо існує окіл цієї точки такий, що із всіх значень, які приймає функція в цьому околі значення в точцінайменше.

Точкою максимуму функції називається точка , якщо існує окіл цієї точки такий, що із всіх значень, які приймає функція в ньому, значення в точцінайбільше.

Критичними називаються точки, в яких або не існує.

Опуклою називається крива АВ, якщо вона розміщена не вище дотичної, проведеної до неї в довільній її точці.

Вгнута крива – це така крива, яка лежить не нижче дотичної, проведеної до неї в довільній її точці.

Точкою перегину графіка функції називають точку, при переході через яку графік функції міняє опуклість на вгнутість або навпаки.

Вертикальною асимптотою графіку функції називається пряма _, якщо при , маємо, що.

Похилою асимптотою графіка функції на, називається пряма, якщо, коли().

Первісною до функції на інтервалі(можна і на відрізку) називається функція_, якщо .

Невизначеним інтегралом називається множина всі первісних функції до заданої функції на інтерваліі позначається

Правильним називається дріб , якщо степінь многочлена чисельника менший за степінь многочлена знаменника.

розбиттям відрізка

Подрібненням розбиття на називається розбиттяцього ж відрізка, якщо воно містить всі точкирозбиття і ще хоча б одну нову.

Рівномірно-неперервною на називається -функція , якщо

Інтегралом Рімана на називається спільне значення чиселі_{, де} ,

_- розбиття відрізка ,

.

Іінтегральною сумою для функції на, для даного– розбиття і даного виборуточокназивається сума виду

Інтегралом Рімана називається

_{якщо вона існує,}

яка не залежить від способу розбиття ні від виборів_.

Криволінійною трапецією називається фігура, обмежена прямими та графіком_.

Площею криволінійного сектора називається границя, коли , суми

(якщо вона існує).

_{Гладкою називається крива, якщо вона задана функцію, яка є неперервною на відрізку разом зі своєю першою похідною.}