4. 1. 2. Заміна змінних у невизначеному інтегралі. Інтегрування за частинами
Досвід, який ми одержали у розв’язуванні попередніх задач, показує, що поки що в нас дуже мало засобів, які б дозволяли ефективно розв’язувати проблему інтегрування. Нижче ми дамо два загальних методи інтегрування, але це складатиме лише невелику частину від тих засобів і прийомів, які ми мали в диференціюванні.
Теорема 1.
Нехай
первісна до
на інтервалі
.
Якщо
– функція, диференційована на
із множиною значень, що належить інтервалу
,
то функція
буде первісною до функції
на
і справедлива рівність:
(1)
Зауважимо, що рівність (1) може застосовуватися двояко:
прочитана справа наліво:
Наприклад.
зліва на право (саме в такому вигляді її називають формулою заміни змінних):
Наприклад.
Доведення.
Доведемо,
що функція
є первісною на інтервалі
до функції. Справді, для
Перша частина доведена.
З умови теореми маємо, що
(2)
(3)
Якщо
в праву частину (2) замість
підставити
то (2) і (3) виявляться рівними, а значить
(1) доведено.
Теорема доведена.
Крім того, інколи ефективним є так-званий метод інтегрування за частинами, який дається наступним твердженням.
Теорема 2.
Нехай
і
диференційовані на інтервалі
функції. Тоді справедлива рівність:
.
Запишемо її в дещо іншому, більш зручному для використання вигляді:
(4)
Саме цю формулу і називають формулою інтегрування за частинами.
Зауважимо, що ця формула не вирішує повністю проблему обчислення інтегралу, вона зводить її до обчислення іншого. І якщо цей інтеграл є табличним або береться якимось способом, то тоді ця формула (4) є ефективною.
Доведення.
Розглянемо
Теорема доведена.
Неважко здогадатися, що методом інтегрування за частинами будуть братися інтеграли від, наприклад, добутку трансцендентних функцій на многочлени, а також від добутку кількох трансцендентних функцій.
Приклад.
Знайти
Розв'язування.
Нехай u
= lnx,
dv
= dx.
Тоді
v
= x
За формулою інтегрування частинами (4) одержимо
Ми поки що розглянули три загальних методи інтегрування: розкладу, інтегрування заміною змінних та за частинами. Проте із цих методів не зовсім очевидно, яким із них брати інтеграл від тієї чи іншої функції (як це було при обчисленні похідних). В зв’язку з цим добре було б дати алгоритми обчислення інтегралів від різних класів функцій. Одним із найголовніших є клас раціональних функцій.
4. 2. Інтегрування різних класів функцій
4. 2. 1. Інтегрування раціональних функцій
Означення
1.
називається раціональною,
якщо вона є часткою двох многочленів
.
,
Для інтегрування таких функцій треба спочатку навчитись інтегрувати наступні чотири класи функцій:
І)
ІІ)
ІІІ)
IV)
Ці функції називаються елементарними дробами відповідно І-IV типів.
Інтеграли від дробів І-ІІ типів беруться «тривіально». Пропонуємо зробити це самостійно.
Тому обчислимо зараз інтеграл від ІІІ типу.
Покажемо, як інтегруються дроби IVтипу.
Тоді для завершення процесу інтегрування слід взяти такий інтеграл:
Для обчислення останнього інтегралу зробимо наступну процедуру:
Таким чином, ми одержали формулу:
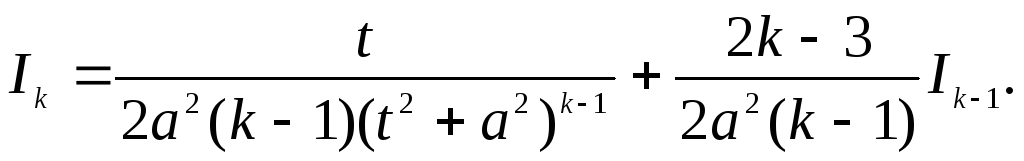
Вона
дозволяє без всякого інтегрування
зводити обчислення
до
.
Кількакратне застосування цієї формули
дозволяє нам звести обчислення
до
.
Цю формулу називають рекурентною
для обчислення інтегралів від дробів
IV
типу.
Приклад.
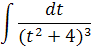
Виявляється, що до обчисленню інтегралів від дробів цих чотирьох типів зводиться інтегрування довільної раціональної функції. Це здійснюється з допомогою наступного алгоритму:
Нехай
маємо
.
З’ясовуємо чи підінтегральна функція є правильним чи неправильним дробом.
(Дріб
називається правильним,
якщо степінь многочлена чисельника
менший за степінь многочлена знаменника.
В протилежному випадку цей дріб
називається неправильним).
Якщо виявиться, що цей дріб неправильний, то потрібно виділити цілу частину і звести його до суми деякого многочлена і правильного дробу.
–правильний.
Остання рівність показує, що інтегрування
неправильного дробу зводиться до
інтегрування многочлена і правильного
раціонального дробу.
Таким чином нам слід навчитись інтегрувати правильні дроби. Розроблена в алгебрі теорія дозволяє хоча б теоретично звести цю процедуру до обчислення інтегралів від простих дробів І-IV типів. Покажемо як використовується теорія на конкретному прикладі. Зауважимо тільки, що перед застосуванням цієї теорії треба многочлен в знаменнику розкласти на так звані незвідні множники.
Нехай маємо такий дріб:
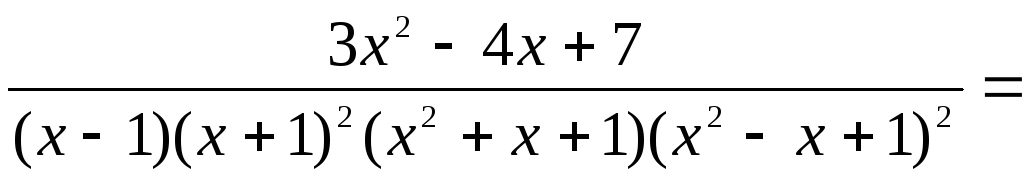
В алгебрі доводиться, що такий дріб можна розкласти як суму наступних простих дробів
.
В
цій рівності коефіцієнти
– невідомі. Їх шукають наступним
способом:
Зводимо праву частину до спільного знаменника, він буде точно таким же як знаменник зліва. З того, що ці дроби тотожно рівні отримуємо, що тотожно рівні чисельники. Але ж чисельники – це деякі многочлени. І для того, щоб вони були рівні, потрібно щоб їхні коефіцієнти були рівними. Зрівнюючи коефіцієнти цих двох многочленів ми одержимо систему рівнянь (в даному випадку із 9 рівнянь), розв’язавши яку (вона завжди сумісна і має єдиний розв’язок) ми знайдемо коефіцієнти.
Такий метод пошуку їх називається методом невизначених коефіцієнтів.
Проілюструємо це на дещо простішому прикладі.
Приклад.
;
M=1
=
+ C.