3. 1. 4. Диференціал функції та його застосування

Нехай – деяка диференційована в точці функція. Це означає, що її приріст можна зобразити у вигляді:

,

Будемо вважати, що

Простий аналіз правої частини рівності підказує, що головний вклад в приріст диференційованої в точці функції вносить перший доданок, який, на відміну від другого, лінійно залежить від . Головна частина диференційованої функції називається диференціалом цієї функції в цій точці і позначається:

Очевидно, що Причому точність тим вища, чим менше . Можна переписати

–формула, яку деколи використовують для обчислення деяких значень функцій.

Наприклад.

.

В проведених вище міркуваннях при введені диференціала в нас була незалежна змінна. Можна домовитись, що розуміти під диференціалом незалежної змінної. Певні роздуми наводять на думку, що в цьому випадку можна покласти рівному . Таким чином, якщо незалежний аргумент, то остаточно запишемо

_.

З’ясуємо, чи збережеться цей вигляд, коли в свою чергу теж є функцією від іншої змінної.

Нехай – диференційована в точці функція і – диференційована в точці функція (). Тоді, як ми знаємо, диференційована в точці і, оскільки тут незалежна змінна, то диференціал цієї функції буде дорівнювати:

Таким чином, ми встановили, що форма диференціала не залежить від того, чи є залежною чи незалежною змінною. Цю властивість диференціала назвали властивістю інваріантності форми диференціала.

3. 1. 5. Похідні і диференціали вищих порядків

Відомо, якщо функція диференційована на деякій множині функція, то на цій множині є в свою чергу теж деякою функцією. Може трапитися, що в деяких точках цієї множини функція має похідну. Її ми назвемо похідною ІІ порядку функції в цих точках і позначимо Аналогічно можна означити і похідну ІІІ порядку – і похідну n-го порядку . ,

Наступна формула вирішує проблему похідної n-го порядку для добутку двох функцій.

Теорема 1 (Формула Лейбніца).

Нехай і – функції n разів диференційовані.

Тоді

Доведення:

Доведемо методом математичної індукції.

1. При

2. Припустимо , що формула вірна при

3. Доведемо, що вона вірна при .

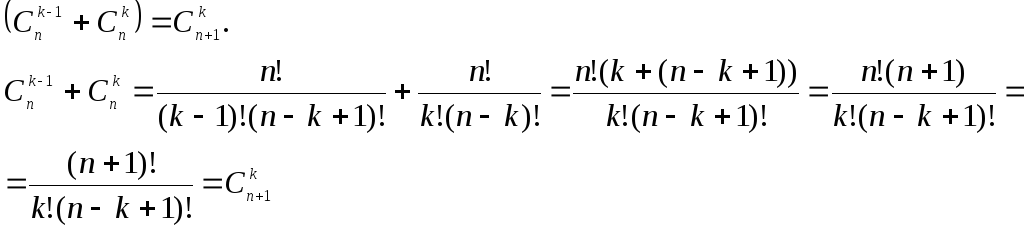
Теорему доведено.

Аналогічно, як ми говорили про похідні вищих порядків, можна ввести поняття і диференціалів вищих порядків.

Означення 1. Диференціалом ІІ порядку функції будемо називати диференціал від диференціала цієї функції.

Спробуємо розібратися при яких умовах, покладених на функцію, має зміст таке означення. Нехай при маємо функцію , де – незалежна змінна, то . Як ми пам’ятаємо , а ми беремо самостійно, тому ні від , ні від функції , ця величина не залежить. Значить ми можемо вважати в цій формулі константою. Може трапитися, що функція в свою чергу також диференційована в точці . Тоді, враховуючи сказане, буде диференційованою в точці функцією. А отже, можна ввести поняття диференціала від цієї функції , який ми і назвемо диференціал ІІ порядку

Аналогічно і вводиться поняття і диференціала n-го порядку.

Означення 2. Якщо функція n разів диференційована в точці , то диференціалом n-го порядку цієї функції в цій точці називається диференціал від диференціала (n-1)-го порядку цієї функції в цій точці.

Найближчою нашою метою є встановити:

• Який вигляд має диференціал n-го порядку;

• Чи залежатиме форма диференціала n-го порядку від того чи залежна чи незалежна змінна.

Отже, нехай – незалежна змінна і n разів диференційована в точці . Тоді, оскільки , то

Міркуючи за індукцією ми встановимо, що в цьому випадку форма диференціала n-го порядку буде такою

Подивимось, чи збережеться ця форма, коли – залежна змінна. Тепер , а є деякою функцією якоїсь іншої змінної. Будемо мати

Наявність 2-го доданка показує, що форма диференціала вже ІІ порядку, коли – залежна змінна, відрізняється від аналогічної у випадку, коли – незалежна змінна. А це означає, що диференціали вищих порядків властивості інваріантності форми не мають.