2. 4. 5. Гіперболічні функції та їх графіки

В математиці часто використовуються функції, які задаються таким чином,

Їх називають відповідно гіперболічним синусом, косинусом, тангенсом і котангенсом. Використовуючи самі означення легко переконатись у справедливості формул

Звідси і так далі.

Введені вище функції називаються гіперболічними, тому що, як ми покладемо (1) і підставимо ці значення в то отримаємо А це означає, що система (1) і рівність (2) – різні вираження однієї і тієї ж кривої в координатній площині, але (2) це рівняння гіперболи. Тому ці функції називають гіперболічними. (Подібно до цього тригонометричні функції можна назвати круговими!)

Побудуємо графіки цих функцій.

1) - неперервна, монотонно зростаюча, непарна на множині дійсних чисел.

2) - монотонно-зростаюча на і монотонно-спадна на неперервна на всій осі, парна.

Графік цієї функції ще називають ланцюговою лінією.

3) - монотонно зростаюча, неперервна на всій осі, непарна.

4) - монотонно спадна на інтервалах та неперервна на об’єднанні цих інтервалів, непарна.

Всі ці властивості і графіки гіперболічних функцій легко одержуються із даних означень цим функціям.

РОЗДІЛ 3.ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ ОДНІЄЇ ЗМІННОЇ

3. 1. Похідна та її обчислення

3. 1. 1. Поняття дотичної до кривої. Кутовий коефіцієнт дотичної

Нагадаємо, що кутовим коефіцієнтом прямої називається кута нахилу цієї прямої до осі (додатній напрям).

В аналітичній геометрії відомо, що якщо пряма проходить через т. і має кутовий коефіцієнт , то рівняння цієї прямої матиме вигляд

.

З’ясуємо далі, що розуміти під дотичною до кривої. Очевидно, що поняття дотичної до кола з геометрії не переноситься буквально на будь-яку криву. І значить, для одержання поняття дотичної до кривої треба вибрати якийсь інший підхід.

Нехай маємо деяку криву. Виберемо на ній точку . Візьмемо на цій кривій ще одну довільну точку , відмінну від . Поведемо січну . Заставимо точку рухатися по кривій до співпадання з точкою . При цьому положення січної буде змінюватися. Якщо існуватиме граничне положення цієї січної (деяка пряма), то її називатимемо дотичною до кривої в точці . З’ясуємо чи завжди існуватиме дотична до кривої.

Наприклад.

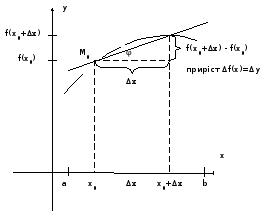
Зрозуміло, що остання крива не матиме в точці [0;0] дотичної, бо не існує такої прямої (єдиної), до якої прямували б січні , якщо точка рухається довільно по кривій до співпадання з точкою . Таким чином ми тільки що показали, що графік функції в точці [0;0] дотичної не має. З’ясуємо далі, як існування дотичної до кривої зв’язане із функцією, графіком якої є ця пряма (крива). Нехай . Надамо приріст Тоді

Далі, очевидно, що існування дотичної до кривої в точці , буде залежати від того, чи існує , тобто, якщо існує , то існуватиме в точці дотична до графіка нашої функції, причому цієї дотичної буде мати вигляд

Таким чином ми встановили, що проблема існування дотичної зв’язана з існуванням останньої границі. До таких границь зводяться багато різних задач (з природи), тому нам потрібно вивчити таку границю незалежно від того, що означає тут.

Нехай – функція, задана в деякому околі точки . Надамо приріст () і перейдемо до точки . (Зауважимо, що ми надаватимемо настільки великим, щоб точки ). Візьмемо і назвемо її приростом функції в точці . Розглянемо .

Означення 1. Якщо існує границя , коли , то вона називається похідною функції в точці і позначається

(або інакше – ).

Означення 1’. Похідна функції в точці – це границя відношення приросту функції в цій точці до приросту аргументу, коли приріст аргументу прямує до нуля.

Таким чином, із розв’язаної вище проблеми про дотичну до кривої і означення похідної, випливає:

Якщо функція має в точці похідну , то графік цієї функції має в точці дотичну, рівняння якої має вигляд

_або