3. 1. 6. Параметрично задані функції і обчислення їх похідних

Нехай маємо дві функції , . Розглянемо систему

Така система інколи задаватиме як функцію від . Зокрема, це буде тоді, коли – строго монотонна на , тоді вона буде оборотною, а значить існуватиме обернена функція . – це явне задання вище написаної, параметрично заданої функції.

Проте далеко не завжди з існування оберненої функції можна одержати аналітичне задання цієї функції (наприклад, на проміжку є монотонно зростаючою, значить оборотною, але виразити звідти через не можна по тій причині, що останнє рівняння не розв’язується відносно ). Таким чином нам треба навчитись брати похідні параметрично заданих функцій, не вдаючись до явного задання цих функцій.

Припустимо, що – диференційовані в точці і . Ми знаємо, що чи залежна чи незалежна змінна, завжди Звідси будемо мати

Очевидно, в останній рівності справа маємо вираз, залежний від , а значить наша похідна теж задається параметрично. Отже має бути залежність від . Вона та сама, що Як наслідок, похідна параметрично заданої функції – це похідна наступної параметрично заданої функції.

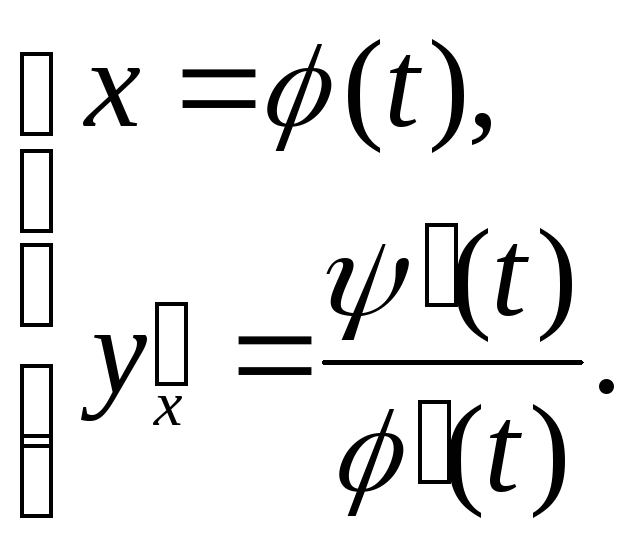
Знайдемо похідну ІІ порядку.

.

Отже, ми одержали, що похідна параметрично заданої функції ІІ порядку, це буде наступна параметрично задана функція.

_.

3. 1. 7. Теореми про середнє. І, іі правила Лопіталя. Критерій строгої монотонності функції

Тут ми доведемо твердження, які дозволять нам в майбутньому одержати різноманітні застосування похідної. Почнемо з наступної теореми, геометричний зміст якої очевидний.

Теорема 1 (Ферма).

Якщо – функція, задана в інтервалі і в точці цього інтервалу вона досягає свого найбільшого або найменшого значення із всіх, які вона набирає в цьому інтервалі, тоді, якщо диференційована в точці , то

(Тобто, при умовах, накладених на функцію в теоремі Ферма, в точці на кривій, що є графіком функції , де функція набуває свого найбільшого або найменшого значення, дотична паралельна до осі ОХ )

Доведення.

Нехай, для конкретності, в точці функція має максимум:

.

Значить тоді

Знайдемо (за теоремою про граничний перехід в нерівностях).

Але ж в точці існує . Значить

З двох останніх нерівностей маємо:

Теорема доведена.

Зауваження 1. Максимум чи мінімум функції слід шукати серед тих точок інтервалу , в яких похідна дорівнює 0 або не існує.

Зауваження 1. Приклад функції показує, що не в кожній точці, де похідна дорівнює 0 буде максимум чи мінімум.

З допомогою першої теореми легко одержується

Теорема 2 (Ролля).

Нехай фунція неперервна на відрізку _, диференційована на інтервалі і , тоді існує точка така, що

Геометричний зміст теореми можна записати так:

При умовах, накладених на функцію в теоремі Ролля, на кривій, що є графіком функції знайдеться принаймні одна точка з координатами , дотична в якій для цієї кривої паралельна до осі ОХ.

Доведення.

Оскільки неперервна на відрізку , то за ІІ теоремою Веєрштрасса, знайдеться дві точки

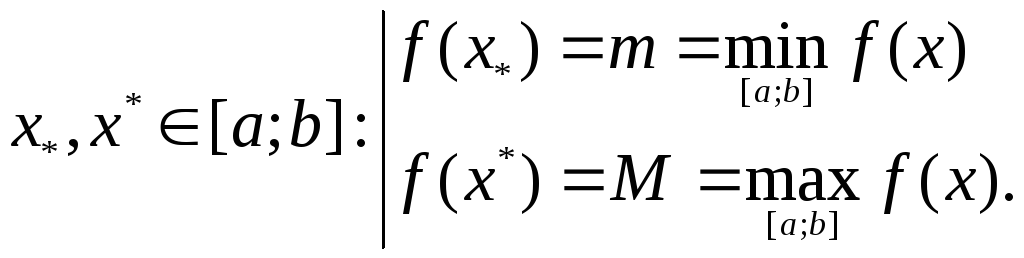
Можливі два випадки:

1) В якості точки можна взяти будь-яку точку з інтервалу .

2) Нехай . Тоді хоча б одна з двох точок або не співпадатиме ні з , ні з , бо в протилежному випадку (тобто якби одна з них дорівнювала , а друга – ) ми мали б, що , а значить – .

Отже, хоча б одна з точок або належить . Нехай для конкретності це буде .Тобто, це точка з інтервалу , де набирає найменшого значення зі всіх. Оскільки на є диференційованою, то існує , а раз так, то за теоремою Ферма матимемо

Теорема доведена.

З допомогою цієї теореми можна довести наступні твердження

Теорема 3 (Лагранжа).

Якщо неперервна на , диференційована на , то існує така, що

Таким чином, використовуючи геометричний зміст похідної і умову паралельності двох прямих, одержимо, що геометрично теорема означає наступне:

При умовах, накладених на функцію в теоремі Лагранжа, на кривій, що є графіком функції знайдеться принаймні одна точка з координатами , дотична в якій для цієї кривої паралельна до хорди, що з’єднує кінці цієї кривої.

Доведення.

Розглянемо таку допоміжну функцію:

, .

1) неперервна на (оскільки неперервна);

2) диференційована на (бо така тут );

3)

Отже, на відрізку , задовольняє всім умовам теореми Ролля, тоді за цією теоремою:

(1)

Звідси, і з (1) одержуємо потрібну нам рівність:

.

Теорема доведена.

Розглянемо деякі наслідки.

Ми знаємо, що похідна від всякої константи дорівнює нулю. Чи вірне обернене твердження?

Наслідок 1. Якщо диференційована на і , то на

Доведення.

Візьмемо . Нехай Тоді а значить на цьому відрізку неперервна, диференційована на , тоді з теореми Лагранжа випливає, що : Але ж , маємо, що А це означає, що Отже Наслідок доведено.

З теореми Лагранжа випливає ще один цікавий наслідок

Наслідок 2. Якщо диференційована на і для , то монотонно неспадна на інтервалі . (Аналогічний наслідок вірний для монотонно не зростаючої функції).

Доведення.

Візьмемо : . Тоді на , (причому ) будуть виконуватися всі умови теореми Лагранжа. Згідно з ними ми будемо мати, що:

З умови маємо, що з вибору точок маємо, що , а отже і

_{Наслідок доведено.}

Аналогічним способом доводиться наслідок 3.

Наслідок 3. Якщо диференційована на і для , то монотонно зростаюча на інтервалі . (Аналогічний наслідок вірний для монотонно спадної функції).

Щодо твердження, оберненого до Наслідку 3, то воно невірне. В цьому нас переконує приклад функції на інтервалі , яка монотонно зростаюча, диференційована на цьому інтервалі, але в точці 0 похідна дорівнює 0. Отже, очевидно, можна стверджувати хіба що таке

Якщо диференційована і монотонно не спадна на , то .

Доведення.

Візьмемо : . Тоді на , (причому ) будуть виконуватися всі умови теореми Лагранжа. Згідно з ними ми будемо мати, що

З умови маємо, що З вибору точок одержимо, що , а отже і . Із довільного вибору точок маємо що .

Останній результат разом з наслідком 2 можна записати у вигляді такого твердження.

Критерій нестрогої монотонності функції на

Для того, щоб диференційована на функція була монотонно неспадною на цьому інтервалі необхідно і достатньо щоб (аналогічно і для незростаючої).

Наступна теорема є узагальненням теорем Лагранжа і одержана з теореми Ролля.

Теорема 4 (Коші).

Якщо і неперервні на і диференційовані на функції і , , то

Зауважимо, що поклавши в цій теоремі , ми одержимо вже доведену теорему Лагранжа.

Доведення.

Покажемо, що Справді, в протилежному випадку ми за теоремою Ролля мали б, що що протирічить умові теореми Коші. Розглянемо допоміжну функцію.

Ця функція задовольняє всі умови теореми Ролля.

1) – неперервна на ;

2) – диференційована на .

3)

Значить за теоремою Ролля

З останніх двох рівностей маємо:

А звідси одержуємо потрібну нам рівність. Теорема доведена.

Зауважимо, що з теореми Ролля, Лагранжа, Коші кожна з них є наслідком іншої. Всі доведені вище теореми об’єднуються спільною назвою ТЕОРЕМИ ПРО СЕРЕДНЄ.

Із теореми Коші одержуються два дуже важливих наслідки, які дозволяють ефективно обчислювати границі функції.

Теорема 5 (І правило Лопіталя).

Нехай в деякому околі точки задано функції і , які мають такі властивості:

1. диференційовані в ньому;

2. в цьому околі;

3. і , коли ;

4. .

Тоді при .

Таким чином ми бачимо, що І правило Лопіталя дозволяє нам розкривати невизначеність .

Доведення.

Візьмемо довільну послідовність з такими властивостями:

1) ;

2) .

Доозначимо і в точці , поклавши . Таким до означенням ми доб’ємося того, що і будуть неперервні в точці , а отже у всьому вказаному в теоремі околі точки . Розглянемо далі відрізок з кінцями . Цей відрізок належатиме повністю нашому околу (один із кінців співпадає з центром околу), а значить, як випливає з умов нашої теореми і проведеного вище до означення – функції і задовольняють на цьому відрізку всім умовам теореми Коші. Тоді, за цією теоремою, знайдеться точка , яка лежить між і така, що . Звідси (Оскільки ) :

; (*)

Нехай , тоді , а значить . Звідси і з умови 4), за означенням Гейне матимемо, що , а з рівності (*) маємо, що . А це означає за означенням Гейне границі функції, що

Теорема доведена.

Зауважимо, що ця теорема вірна і у випадку, коли , будь-якого знаку. Ця ж теорема буде вірною і у випадку, коли .

Є ще одне правило Лопіталя, яке розкриває невизначеність .

Теорема 6 (ІІ правило Лопіталя).

Нехай в деякому задано дві функції і з такими властивостями:

1. диференційовані в ньому;

2. в цьому околі;

3. і , коли ;

4. .

Тоді при .

Зауважимо, що в обох правилах, якщо не існує , то звідси не можна стверджувати, що не існуватиме . В другому правилі, як і в першому і можуть бути нескінченностями будь-якого знаку.

Правила Лопіталя можна використовувати безпосередньо для розкриття вказаних вище двох невизначеностей. Проте вони є часто ефективними при розкритті інших невизначеностей.

1) ;

2) ;

3) ;

4) ;

5) .

Теорема 7 (Критерій строгої монотонності функції)

Для того, щоб функція , диференційована на проміжку , була монотонно-зростаючою на ньому, необхідно і достатньо, щоб

1) ;

2) ніякі точки цього проміжку, в яких похідна дорівнює нулю, не утворювали відрізка.

Доведення.

Необхідність.

Нехай монотонно-зростаюча на , тоді одержимо, що (оскільки, якщо зростаюча, то вона монотонно неспадна, а для монотонно неспадної диференційованої функції завжди ).

Покажемо, що виконується друга умова. Нехай точки, в яких похідна дорівнює нулю, або частина цих точок, утворює деякий відрізок : Значить, за відомим наслідком В результаті ми одержали протиріччя з тим, що вона на цьому відрізку має бути монотонно-зростаючою.

Достатність.

Нехай виконуються умови 1) і 2). Покажемо, що монотонно-зростаюча на . З умови 1) маємо, що монотонно-неспадна на Припустимо, що існують точки . Звідси, в силу монотонного не спадання функції на зразу випливає, що на всьому відрізку набирає одного і того ж значення. Отже тут , а значить її похідна на цьому відрізку дорівнює нулю. А це протирічить 2) –умові достатності.

Теорема доведена.

Приклад.

Дослідити на монотонність функцію

Проміжки спадання –

Проміжок зростання –